マーライオン再び〜ラグランジュの未定乗数法を用いて〜

この記事は、日曜数学 Advent Calendar 2016 - Adventar 19日目の記事です。18日目はふにゅさんのガロアがイケメンな件―数学とイメージの関係 - funyuのブログです。

ガロア、いいですね。私は男なのでガロアに恋心を抱くことはありませんが、ガロア理論の基本定理には恋心を抱いてしまいそうです。これまで数論を勉強してこなかったので、ガロア理論が大いに使われていそうな数論を勉強するのが今の楽しみです。

はじめに

以前下記の記事でマーライオンが一番遠くまで水を飛ばすことのできる口の角度を求めました。

mattyuu.hatenadiary.com

前回は空気抵抗を無視しましたが、今回は空気抵抗も考慮して問題を解きます。空気抵抗が入るだけで、問題がぐっと難しくなり、前回と同様の方法では解けませんでした。しかし、ラグランジュの未定乗数法という手法を用いることで、最適解 $\theta_{\rm max}$ の満たすべき方程式を得ることができましたので、問題を解きながらラグランジュの未定乗数法の強力さを紹介したいと思います。

この記事では前回必要だった高校物理の力学の知識、高校の数Ⅲで習う三角関数の微分の知識に加えて、微分方程式の基礎(変数分離法のみ)、偏微分、指数関数、対数関数の微積分の知識も前提としてしまいます(大学初年度レベルです。)。逆に言うと、数学の知識が増えると解ける問題の範囲も広がるということなので、数学を勉強するモチベーションにもなりますね。

前提知識がない方は、前回同様フジテレビのガリレオで福山雅治さんはこんな数式を書いていたんじゃないか？と想像しながら、数式を流し読みしていただけたら面白いのではないかと思います。

問題設定

では、問題設定から行いましょう。

f:id:mattyuu:20161218123227j:plain
f:id:mattyuu:20161218123235j:plain

前回と同様に、水は大きさのない質点として計算していきます。水は常に連続的に噴射され続けていますが、時刻 $t=0$ で質量 $m$ の水分子が1粒発射されたものとして読んでください。また空気抵抗は速さに比例する大きさの力が、運動の方向と逆向きに働くものとします。

では前回と同じ方法で解けるところまで解いていきましょう。口から飛び出る水の速度を水平方向(x軸右方向)の速度 $v_x$ と、垂直方向(y軸上方向)の速度 $v_y$ に分けて、ニュートンの運動方程式を立てます。

$\displaystyle \begin{cases} m\frac{{\rm d}v_x(t)}{{\rm d}t} = -kv_x \rightarrow \frac{{\rm d}v_x(t)}{{\rm d}t} = -k^{\prime}v_x\\ \\ m\frac{{\rm d}v_y(t)}{{\rm d}t} = - mg -kv_y \rightarrow \frac{{\rm d}v_x(t)}{{\rm d}t} = -g -k^{\prime}v_y \end{cases}$

ここで、記載の簡略化のため、 $k^{\prime}=k/m$ と置いています。出発点となる運動方程式から $k$ 、 $m$ が消えたため、今後 $k$ 、 $m$ は用いず、 $k^{\prime}$ のみを用いることになります。 $k^{\prime}$ が大きいほど、空気抵抗の影響が大きくなります。

$v_x(t)$ 、 $v_y(t)$ の導出

$v_x$ と $v_y$ の微分方程式をそれぞれ変数分離法で解き、 $v_x(t)$ 、 $v_y(t)$ を導出します。

まずは、 $v_x(t)$ です。

$\displaystyle \begin{split} & \frac{{\rm d}v_x}{v_x}=-k^{\prime}{\rm d}t \\ & \\ & \rightarrow \int_{v_x(0)}^{v_x(t)} \frac{{\rm d}v_x}{v_x} = -k^{\prime}\int_0^t{\rm d}t \\ & \\ & \rightarrow \log{v_x(t)}-\log{\left(v\cos{\theta}\right)}=-k^{\prime}t \\ & \\ & \rightarrow v_x(t) = v\cos{\theta}\cdot e^{-k^{\prime}t} \end{split}$

次に、 $v_y(t)$ を求めます。

$\displaystyle \begin{split} & \frac{{\rm d}v_y}{g+k^{\prime}v_y}=-{\rm d}t \\ & \\ & \rightarrow \int_{v_y(0)}^{v_y(t)} \frac{{\rm d}v_y}{g+k^{\prime}v_y} = -\int_0^t{\rm d}t \\ \\ & \rightarrow \frac{1}{k^{\prime}}\log{\left(g+k^{\prime}v_y(t)\right)}-\frac{1}{k^{\prime}}\log{\left(g+k^{\prime}v\sin{\theta}\right)}=-t \\ \\ & \rightarrow g+k^{\prime}v_y(t)=\left(g+k^{\prime}v\sin{\theta}\right) \cdot e^{-k^{\prime}t} \\ \\ & \rightarrow v_y(t)=v\sin{\theta}\cdot e^{-k^{\prime}t} -\frac{g}{k^{\prime}}\left(1-e^{-k^\prime t}\right) \end{split}$

無事、 $v_x(t)$ 、 $v_y(t)$ が求まりました。

$\displaystyle \begin{cases} v_x(t) = v\cos{\theta}\cdot e^{-k^{\prime}t}\\ \\ v_y(t) = v\sin{\theta}\cdot e^{-k^{\prime}t} -\frac{g}{k^{\prime}}\left(1-e^{-k^\prime t}\right) \end{cases}$

$x(t)$ 、 $y(t)$ の導出

次に、 $v_x(t)$ 、 $v_y(t)$ をそれぞれ $t$ で積分して、時刻 $t$ での水の位置 $(x(t),y(t))$ を求めましょう。

まずは、 $x(t)$ から。

$\displaystyle \begin{split} & x(t) = \int_0^t v_x(t){\rm d}t = \int_0^t v\cos{\theta}\cdot e^{-k^{\prime}t} {\rm d}t \\ & \\ & \qquad = \frac{v\cos{\theta}}{k^{\prime}}\left(1-e^{-k^{\prime}t}\right) \end{split}$

次に、 $y(t)$ です。

$\displaystyle \begin{split} & y(t) = h + \int_0^t v_y(t){\rm d}t = \int_0^t \left(v\sin{\theta}\cdot e^{-k^{\prime}t} -\frac{g}{k^{\prime}}\left(1-e^{-k^\prime t}\right)\right) {\rm d}t \\ & \\ & \qquad = h + \frac{v\sin{\theta}}{k^{\prime}}\left(1-e^{-k^{\prime}t}\right)-\frac{g}{k^{\prime}}t+\frac{g}{{k^{\prime}}^2}\left(1-e^{-k^{\prime}t}\right) \end{split}$

前回よりはるかに複雑ですが、 $x(t)$ 、 $y(t)$ も求まりました。

$\displaystyle \begin{cases} x(t) = \frac{v\cos{\theta}}{k^{\prime}}\left(1-e^{-k^{\prime}t}\right) \\ \\ y(t) = h + \frac{v\sin{\theta}}{k^{\prime}}\left(1-e^{-k^{\prime}t}\right)-\frac{g}{k^{\prime}}t+\frac{g}{{k^{\prime}}^2}\left(1-e^{-k^{\prime}t}\right) \end{cases}$

空気抵抗がない場合は、この $x(t)$ 、 $y(t)$ を連立させ $t$ を消去することで、 $x$ と $y$ の関係を $y=ax^2+bx+c$ という二次関数(=放物線)の形で表すことができましたが、式の形を見ればわかる通り空気抵抗がある場合では二次関数で表すことができません。マーライオンの口から発射された水は、空気抵抗が入ることで放物線とは異なる軌道を描くことなります。

せっかく $x(t)$ 、 $y(t)$ が求まりましたので、ここで一休みしてその軌道を見てみましょう。空気抵抗を大きくする程その軌道は歪曲され、遠くまで飛ばなくなることがわかりますね。

f:id:mattyuu:20161218112702g:plain

地面に落ちる時間が求められない

前回は $y(t)=0$ を解いて、水が地面に落ちる時刻 $T$ を求め、そこから水平到達距離 $L$ を $\theta$ の関数で表し、それを微分することで最適解 $\theta_{\rm max}$ を求めました。しかし、今回は最初の関門である $y(t)=0$ が解ける気がしません。 $y(t)$ の中には $t$ の一次関数と指数関数が共に現れています。例えば私は、次のようなシンプルな方程式も解析的に解くことができません。*1

$\displaystyle x+e^{x}=0$

そして、解析的に解くことを諦めて、 $y(t)=0$ をコンピュータを使って数値的に解いたとしても、数値解は離散的にしか求められないため、その先の水平到達距離 $L$ を $\theta$ で微分をするところで行き詰まるでしょう。

私はここでこの問題を解くことを諦めかけました。

しかし、諦めきれず式をいじくり回しているときに、だんだんと頭の片隅から蘇ってくるものがありました。それがラグランジュの未定乗数法だったんです。

ラグランジュの未定乗数法

ここでは、一瞬マーライオンを忘れて、ラグランジュの未定乗数法の紹介をします。(変数の記号は今回の問題に合わせて $t$ と $\theta$ で記載しています。)

ラグランジュの未定乗数法
$g(t,\theta)=0$ という条件の下、 $f(t,\theta)$ を最大化したいとき、
$F(t,\theta,\lambda)=f(t,\theta)-\lambda g(t,\theta)$
とおくと、下記の連立方程式の解が、その最適解の候補を与える。

$\displaystyle \begin{cases} \frac{\partial F}{\partial t}(t,\theta,\lambda) = 0 \\ \\ \frac{\partial F}{\partial \theta}(t,\theta,\lambda) = 0 \\ \\ \frac{\partial F}{\partial \lambda}(t,\theta,\lambda) = 0 \\ \end{cases}$

2変数の問題なのに、わざわざ変数 $\lambda$ を付け加えて3変数にしているのがミソです。大学初年度で習う陰関数定理を用いれば証明が出来ますが、ここでは証明は行いません*2。

さて、このラグランジュの未定乗数法がなぜ今回の問題に関係あるのでしょうか。

先ほど $x(t)$ 、 $y(t)$ と、あたかも $t$ だけの関数のように $x$ 、 $y$ を書き下しましたが、この問題では一番遠くまで飛ばす $\theta$ を求めるという意味で、 $\theta$ も変数と考えた方が都合がよく、 $x(t,\theta)$ 、 $y(t,\theta)$ と書いた方がより適切です( $h$ 、 $v$ 、 $g$ 、 $k^\prime$ も値を変更することができますが、ここでは定数という位置付けです。パラメータと呼んだ方がいいかもしれません。)。

先ほど解くことを諦めた $y(t,\theta)=0$ という方程式に注目しましょう。これはある角度 $\theta$ で発射された水が地面に落ちる時刻 $t$ を求める方程式と考えてきましたが、逆に時刻 $t$ で地面に落ちるように口の角度 $\theta$ を求める方程式と考えることもできます。その意味で $t$ と $\theta$ は全く対等です。

$y(t,\theta)=0$ を満たす $(t^{\ast},\theta^{\ast})$ は、口の角度が $\theta^{\ast}$ のとき、時刻 $t^{\ast}$ で地面に水が地面に落ちているということを意味します。このような $(t^{\ast},\theta^{\ast})$ の組の中で $x(t^{\ast},\theta^{\ast})$ を最大にするものを求めると、その $\theta^{\ast}$ が求めたい最適の角度 $\theta_{\rm max}$ になります。つまり、 $y(t,\theta)=0$ という条件の下、 $x(t,\theta)$ を最大化したいのです。これはラグランジュの未定乗数法の前提そのものですね。

簡単な例

今回の問題をラグランジュの未定乗数法で解く前に、とても簡単な例題を解くことで前回の空気抵抗なしの場合の解法と、この後に行う今回の解法の比較をしてみましょう。

問題
$g(t,\theta)=t-\theta^2=0$ という条件の下、 $f(t,\theta)=2\theta-t+4$ を最大化しましょう。

ではまず、前回の解法から。

直接的な解法
$g(t,\theta)=t-\theta^2=0$ より $t=\theta^2$ となる。これを $f(t,\theta)=2\theta-t+4$ に代入して、
$f(t,\theta)=-\theta^2+2\theta+4=-(\theta-1)^2+5$
となるから、 $\theta=1$ 、 $t=1$ のとき、最大値 $5$ をとる。

この解法は $g(t,\theta)=0$ の条件から $t=\tilde{g}(\theta)$ のように $t$ を $\theta$ で表して、 $\tilde{f}(\theta)=f\left(\tilde{g}(\theta),\theta\right)$ という風に $f$ を $\theta$ だけの関数で表すことで、通常の1変数関数の最大値問題に帰着させています。この解法の肝は $t=\tilde{g}(\theta)$ と $t$ を $\theta$ の関数で表せたことになります。しかし空気抵抗がある場合のマーライオンの問題のようにそれはいつも可能とは限りません。

では、ラグランジュの未定乗数法を用いた解法を見てみましょう。

ラグランジュの未定乗数法による解法
$F(t,\theta,\lambda)\equiv f(t,\theta)-\lambda g(t,\theta)=2\theta-t+4 - \lambda(t-\theta^2)$ とする。

ラグランジュの未定乗数法より、最適解を得るには下記の連立方程式を解けばよい。

$\displaystyle \begin{cases} \frac{\partial F}{\partial t}(t,\theta,\lambda) = -1-\lambda = 0 \\ \\ \frac{\partial F}{\partial \theta}(t,\theta,\lambda) = 2+2\lambda\theta = 0 \\ \\ \frac{\partial F}{\partial \lambda}(t,\theta,\lambda) = -t+\theta^2 = 0 \\ \end{cases}$

第1式より $\lambda=-1$ 、これを第2式に代入して $\theta=1$ 、そして第3式より $t=1$ を得る。
最大値は $f(1,1)=5$ となる*3。

先の解法とは全く違うのに、これで同じ解が得られることに驚きます。

ラグランジュの未定乗数法を用いて解く

さて、いよいよ本来の問題を解くときがきました。まず、条件 $g(t,\theta)=0$ の $g(t,\theta)$ を次で定義します。

$\displaystyle g(t,\theta)\equiv {k^{\prime}}^2y(t,\theta)={k^{\prime}}^2h + k^{\prime}v\sin{\theta}\left(1-e^{-k^{\prime}t}\right)-{g}k^{\prime}t+g\left(1-e^{-k^{\prime}t}\right)$

$g(t,\theta)=y(t,\theta)$ としてもよいのですが、定数 ${k^{\prime}}^2$ をかけることで記載が簡易になるようにしています。

最大化する $f(t,\theta)$ も $x(t,\theta)$ に $k^{\prime}$ をかけて、次式で、

$\displaystyle f(t,\theta)\equiv k^{\prime}x(t) = v\cos{\theta}\left(1-e^{-k^{\prime}t}\right)$

また、関数 $F(t,\theta,\lambda)$ を、次式で、

$\displaystyle \begin{split} & F(t,\theta,\lambda)\equiv f(t,\theta)-\lambda g(t,\theta) \\ & \\ & \qquad = v\cos{\theta}\left(1-e^{-k^{\prime}t}\right)-\lambda\left({k^{\prime}}^2h + k^{\prime}v\sin{\theta}\left(1-e^{-k^{\prime}t}\right)-{g}k^{\prime}t+g\left(1-e^{-k^{\prime}t}\right)\right) \end{split}$

それぞれ定義します。

関数の準備が整いました。ラグランジュの未定乗数法を用いると、解くべき連立方程式は下記になります。

$\displaystyle \begin{cases} \frac{\partial F}{\partial t}(t,\theta,\lambda) = k^{\prime}v\cos{\theta}\cdot e^{-k^{\prime}t} -\lambda\left({k^{\prime}}^2v\sin{\theta}\cdot e^{-k^{\prime}t}-{g}k^{\prime}+gk^{\prime}e^{-k^{\prime}t}\right) = 0 \\ \\ \frac{\partial F}{\partial \theta}(t,\theta,\lambda) = -v\sin{\theta}\left(1-e^{-k^{\prime}t}\right) -\lambda k^{\prime}v\cos{\theta}\left(1-e^{-k^{\prime}t}\right)= 0 \\ \\ \frac{\partial F}{\partial \lambda}(t,\theta,\lambda) = -\left({k^{\prime}}^2h + k^{\prime}v\sin{\theta}\left(1-e^{-k^{\prime}t}\right)-{g}k^{\prime}t+g\left(1-e^{-k^{\prime}t}\right)\right) = 0 \\ \end{cases}$

それでは、解いていきましょう。まずは $t\neq 0$ に注意して、第2式より、

$\displaystyle \lambda = -\frac{\tan{\theta}}{k^{\prime}}$

を得ます。いきなり $\lambda$ がわかりました。幸先のよいスタートです。

次に、得られた $\lambda$ を第1式に代入して、

$\displaystyle k^{\prime}v\cos{\theta}\cdot e^{-k^{\prime}t} +\frac{\tan{\theta}}{k^{\prime}}\left({k^{\prime}}^2v\sin{\theta}\cdot e^{-k^{\prime}t}-{g}k^{\prime}+gk^{\prime}e^{-k^{\prime}t}\right) = 0$

となり、この両辺に $\cos{\theta}$ をかけて整理すると、

$\displaystyle \begin{split} & k^{\prime}v\cos^2{\theta}\cdot e^{-k^{\prime}t} +k^{\prime}v\sin^2{\theta}\cdot e^{-k^{\prime}t}-g\sin{\theta}+g\sin{\theta}\cdot e^{-k^{\prime}t} = 0 \\ & \\ & \rightarrow k^{\prime}ve^{-k^{\prime}t} +g\sin{\theta}\cdot e^{-k^{\prime}t}=g\sin{\theta} \\ & \\ & \rightarrow e^{-k^{\prime}t} = \frac{g\sin{\theta}}{k^{\prime}v+g\sin{\theta}} \\ & \\ & \rightarrow t=\frac{1}{k^{\prime}}\log{\frac{k^{\prime}v+g\sin{\theta}}{g\sin{\theta}}} \end{split}$

形は複雑ですが、 $t$ を $\theta$ の式で求めることができました。では、最後にこれを第3式に代入して整理しましょう。

$\displaystyle \begin{split} & {k^{\prime}}^2h+k^{\prime}v\sin{\theta} \frac{k^{\prime}v}{k^{\prime}v+g\sin{\theta}} - g\log{\frac{k^{\prime}v+g\sin{\theta}}{g\sin{\theta}}} + \frac{gk^{\prime}v}{k^{\prime}v+g\sin{\theta}} = 0 \\ & \\ & \rightarrow {k^{\prime}}^2h\left(k^{\prime}v+g\sin{\theta}\right)+{k^{\prime}}^2v^2\sin{\theta}-g\left(k^{\prime}v+g\sin{\theta}\right)\log{\frac{k^{\prime}v+g\sin{\theta}}{g\sin{\theta}}}+gk^{\prime}v = 0 \end{split}$

あとは、これを $\theta$ について解くだけなのですが、見るからに無理そうです。この方程式を満たす $(0,\pi/2)$ の範囲の解が、求めたい最適解 $\theta_{\rm max}$ になります*4。

最後の最後で数値解になってしまうことは口惜しいですが、仕方ありません。

最後の式の左辺を $\theta$ ではなく、一般の変数 $x$ の関数 $f(x)$ とみなして、demosで $y=f(x)$ のグラフを描いてみましょう。

f:id:mattyuu:20161218110018p:plain

$k^{\prime}$ 、 $h$ 、 $v$ 、 $g$ のパラメータをいじることで、関数のグラフは形を変えますが、確かに $(0,\pi/2)$ の範囲に1つだけ解がありそうです。

そして、 $k^{\prime}$ を大きくしていくと、最適解 $\theta_{\rm max}$ は小さくなっていきます。これは $h=0$ の場合によく知られている事実と合致します。
f:id:mattyuu:20161218110457g:plain

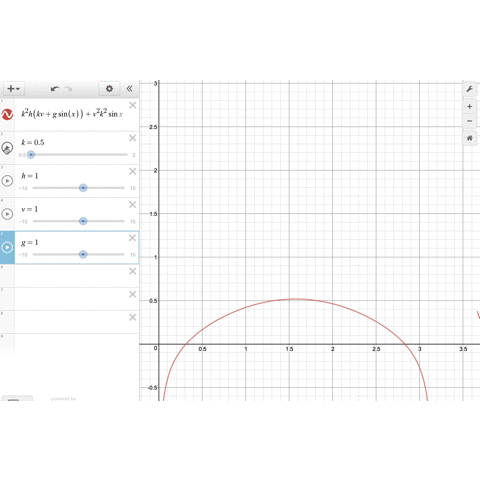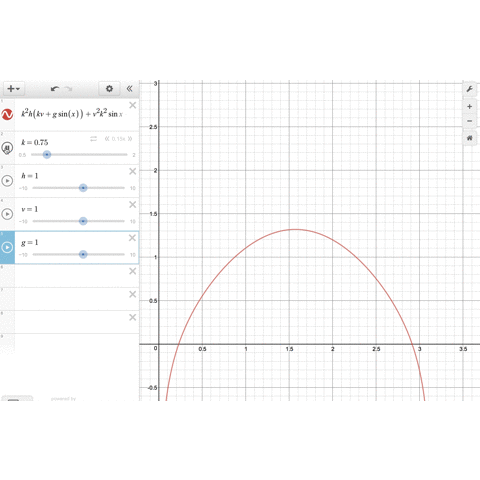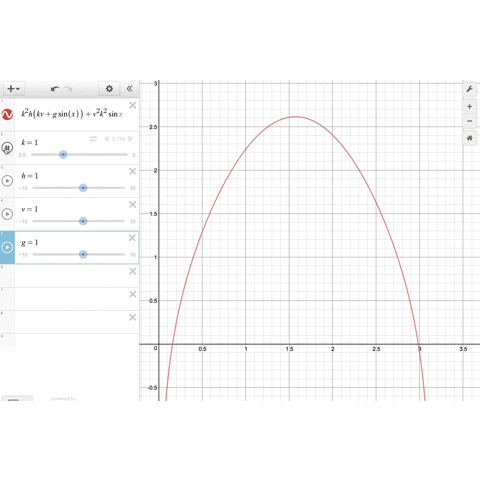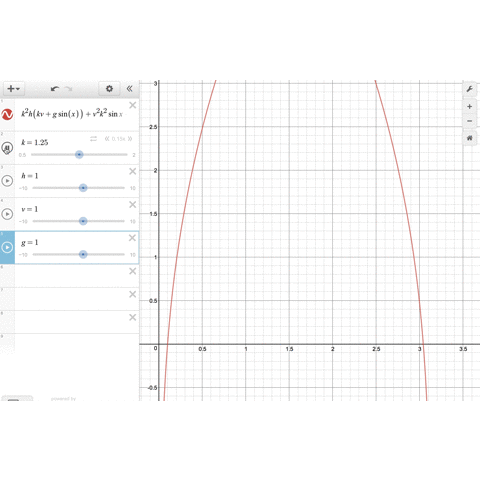
demosで確かめる

残念ながらdesmosには方程式をsolveする機能はありませんので、パラメータを連続的に動かした時の最適解 $\theta_{\rm max}$ をdesmos上だけで変動させて表示させることはできません。パラメータを固定して $\theta_{\rm max}$ を数値計算で求め、desmosを使って実際に最適解が得られていそうということを確認します。前回同様、マーライオンにいろいろな角度で水を発射してもらい、飛距離が最大になる最適解の角度の方向にはオレンジ色の点線を引き、最大到達地点 $x(\frac{1}{k^{\prime}}\log{\frac{k^{\prime}v+g\sin{\theta_{\rm max}}}{g\sin{\theta_{\rm max}}}},\theta_{\rm max})=\frac{v^2\cos{\theta_{\rm max}}}{k^{\prime}v+g\sin{\theta_{\rm max}}}$ には赤い旗を置いておきましょう。そして、比較のため空気抵抗がない場合の軌道を紫色の点線で表示します。

下記の例では、 $k^{\prime}=0.2$ 、 $h=1$ 、 $v=2$ 、 $g=1$ としました。その時の $\theta_{\rm max}$ はおよそ $0.56$ となります。

f:id:mattyuu:20161218115515g:plain

うまくいってますね!

まとめ

最後の最後は数値解になってしまいましたが、ラグランジュの未定乗数法を用いて曲がりなりにも最適解 $\theta_{\rm max}$ を求めることができました。最後に得られた式を使って、空気抵抗がある場合は最適な角度は常に下方に修正されるのか、といったことを調べたら面白いと思うのですが、今回はこの辺りにしておきます。

空気抵抗なし版の問題もラグランジュの未定乗数法を用いて、前回と同じ解析解を得ることができます。やってみるとラグランジュの未定乗数法を用いる方が遥かに簡単でした。一度計算してみたら面白いと思います。

ラグランジュの未定乗数法は大学で習っており、「あぁ、そんなものもあるんだなぁ、便利そうだなぁ」くらいの印象でした。しかし自分が問題設定してラグランジュの未定乗数法を使わないと解けない問題に出会うとその凄さに驚嘆せずにはおれません。「あぁ、楽しい計算だったなぁ」

f:id:mattyuu:20161218123247j:plain