まず最初に投稿が遅れてしまったことをお詫び申し上げます。来年アドベントカレンダーに参加する場合は、11月時点で書く内容が固まっているテーマで登録させていただきます。申し訳ありませんでした。
はじめに
今回日曜数学のアドベントカレンダーのテーマを考えている中で頭に思い浮かんだものがエドワード・フレンケル教授著の「数学の大統一に挑む」でした。
- 作者: エドワード・フレンケル,青木薫
- 出版社/メーカー: 文藝春秋
- 発売日: 2015/07/13
- メディア: 単行本
- この商品を含むブログ (7件) を見る
概要をAmazonから抜粋すると下記の通りとなっており、フレンケル教授の幼少からの成長を描写しながら、教授が直面した数学の概念を一般向けに解説する形となっています。
憧れのモスクワ大学の力学数学部の試験に全問正解したにもかかわらず父親がユダヤ人であるために不合格。それでも少年は諦めず、数学を学び続けた。「ブレイド群」「リーマン面」「ガロア群」「カッツ・ムーディー代数」「層」「圏」…、まったく違ってみえる様々な数学の領域。しかし、そこには不思議なつながりがあった。やがて少年は数学者として、異なる数学の領域に架け橋をかける「ラングランズ・プログラム」に参加。それを量子物理学にまで拡張することに挑戦する。ソ連に生まれた数学者の自伝がそのまま、数学の壮大なプロジェクトを叙述する。
この本は発売時に購入して読んだのですが、その時から心にひっかかっていたものがあります。それは大学生になったフレンケルが挑んだ数学の未解決問題についてです。
人種差別によりモスクワ大学に入学できなかったフレンケルですが、フェンスを乗り越えてでもモスクワ大学に侵入し、数学の授業を受けていました。そんな熱意を買われたのか世界的数学者ヴァルチェンコから有名数学者フックスとの共同研究を勧められます。大学入試で絶望にフレンケルに奇跡のような出来事であり、実際にフックスに会い、読むべき論文を手渡された場面では、
わたしは聖杯を授かったような気持だった
という描写がされています。数学の論文を聖杯と例える気持ちは数学好きであれば分かるのではないでしょうか。この本にはこういった美しい描写が随所に現れており、読むと心がときめきます。
フレンケルはおよそ2カ月をかけてこの未解決問題を解決します。様々なアプローチを試し、ついに問題が解けた瞬間は、
ところが突如として、まるで黒魔術でも使ったかのように、すべてが明らかになった。一挙にジグソーパズルが組み上がり、美しくエレガントな絵の全貌が現れたのだ。あの瞬間のことを、私はけっして忘れないだろう。あの経験は永遠に、わたしの宝物であり続けるだろう。
と描写されています。どうですか?こんなに熱い描写をされると、フレンケルが証明したものが何か気になりませんか?
この本はあくまで一般書であり、細かい数式は出てきません。私はフレンケルが証明したものを数学的に理解せずに読んでいたため、何を証明したのだろうという事がずっと心にひっかかっていました。
今回の記事の内容と今後の展望。。。
ということで、21才のフレンケルが証明したものを紹介したかったのですが、フレンケルの論文(たった3ページ!)を購入し、実際にその分野(代数的トポロジー)の数学を調べてみるとわからない用語が多すぎて理解できませんでした。ただそれでは悔しいので勉強を続けながら何回かの記事に分けて紹介させていただきます*1。そこで今回は、
・フレンケルが証明したもの
・なぜそれが重要か
・ブレイド群とその交換子群
・判別式が0でない多項式の空間の基本群
について紹介したいと思います。
フレンケルが証明したもの
フレンケルが証明したもの、それはブレイド群■
驚くことはこんなところにもオイラーの関数が現れることです。フレンケルも
その答えは予想もしなかったもので、フックスと私が考えていた以上に興味深いものだった」と語っています。
ただ、私のレベルではこの結果を見ても疑問がわきます。
・ベッチ数はホモロジー群のランクで定義されるのではないか?
・「群のコホモロジー」のwikipediaを見ると群と
加群
に対して、コホモロジー群
を定義するが、
への
の作用がそもそもどう定義されるかがわからない。
前者に関してはポアンカレ双対 - Wikipedia
が、後者に関しては普遍係数定理 - Wikipediaが絡んでいる気がするのですが、今時点では私の理解が全く及んでいません。。。全く思い違いの解釈をしているかもしれません。今後の勉強で明らかにしていきます。
主張すら理解できないのは本当に情けないですが、勉強するきっかけになるのでよかったと強がっておきます。
フレンケルが証明したものの重要性
ここも現時点での私の解釈です。間違っている可能性もあります。
まず最初に「数学者は様々な位相多様体を位相不変量によって分類したい」という根源的な欲求を持っているとさせていただきます*2。
次に最高次の係数がで相異なる
個の複素数解をもつ複素係数多項式全体の集合を
とします。つまり、
です。ここでは多項式に対してその判別式を返す関数です。多項式が重解を持つことと多項式の判別式が
になることが同値のため、このように書けます。
多項式は昔から数学の世界で活躍してきましたし、重解の有無も多項式の重要な性質になりますので、このような空間がどのような空間なのかを研究したくなる気持ちはわかるでしょう。
の元はその解となる
個の相異なる複素数を指定することで一意に決まりますから*3、
は順序を持たない互いに異なる
個の複素数の組全体からなる空間と同一視できます。実際に位相を入れて証明していないですが、
が複素
次元の位相多様体になることは明らかでしょう*4。
また、は判別式が
でない多項式全体の空間ですが、そうなると判別式がある特定の値
であるような
の部分空間(ここでは
と書く)がどのような空間であるかということにも興味がわくでしょう。
そのような興味の下、フレンケルが証明したものの重要性がわかるストーリーは下記の通りです*5。
や
を詳しく知りたい!
- 位相多様体を詳しく知ること、それは位相不変量を知ることだ!
- ということで
や
のベッチ数(←位相不変量)を知りたい!
- 一般に群
に対して位相空間
がある条件を満たすとき、
は
の分類空間と呼ぶのだが、なんと
は
の、
は
の分類空間になっている!
- なので
や
のコホモロジーを知りたい!
本記事の残りではまだ定義すらしていない謎の群、
を紹介します。その後
、
がそれぞれ
、
の基本群になっていることを直感的に説明します*6。その動機としては
が
の分類空間となる必要条件として、
の基本群が
と同型になることがあるためです。
ブレイド群とは
(ただし、
)
(ただし、
)
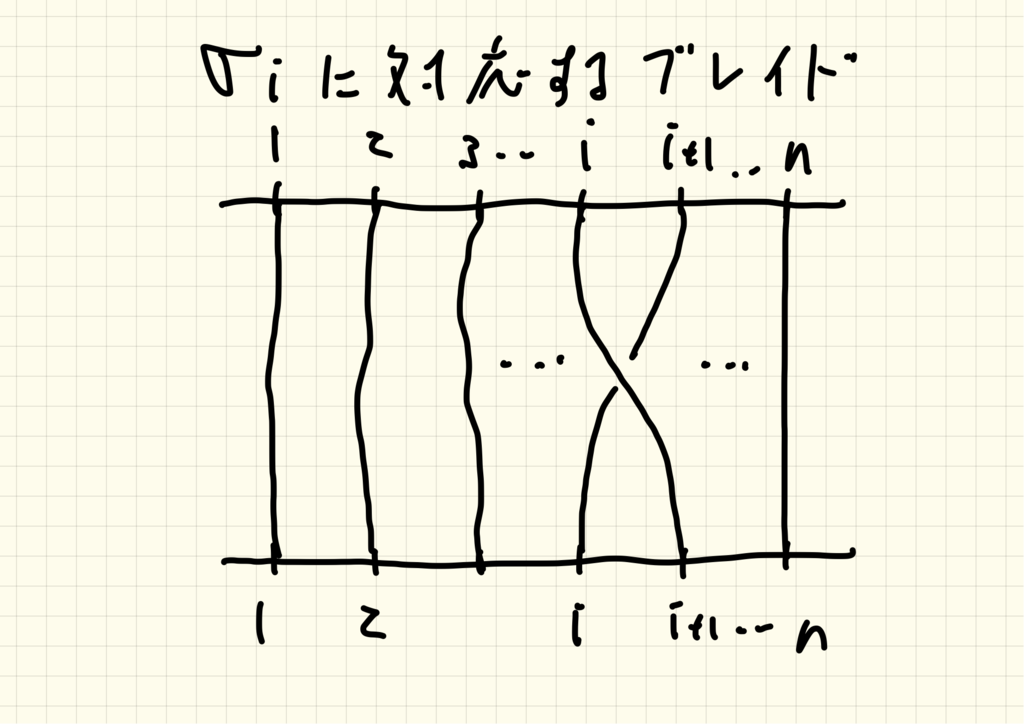
これは下記のように考えると視覚的に理解できる群になります。
枚の板にそれぞれ
本のくぎを打ちつけ、板とは別に
本の紐を用意します。「同じくぎに2本以上の紐を結ぶこと」、「紐が自分自身と交差すること」を禁止し、
個の板を
本のひもで結びます。その紐の結び目の様子*7と
の元が1対1に対応します。この
枚の板と
本の紐の組をブレイドと呼ぶことにします。

つのブレイドの和及び、
に対応するブレイドに関しても次の図のように定めることで、演算も含めて
とブレイドの集合が完全に対応します。

そう考えると次のように生成元の間の関係も視覚的に理解できます。元々はブレイドとして誕生し、その本質が
個の生成元とその間の関係式という形で改めて定義されたのです。
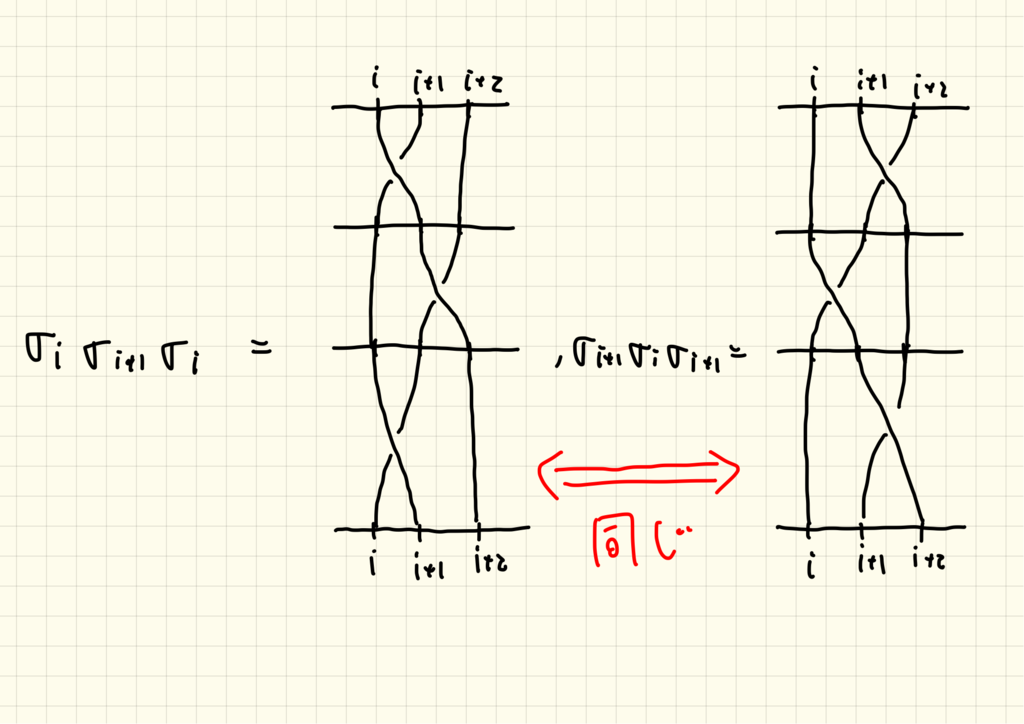
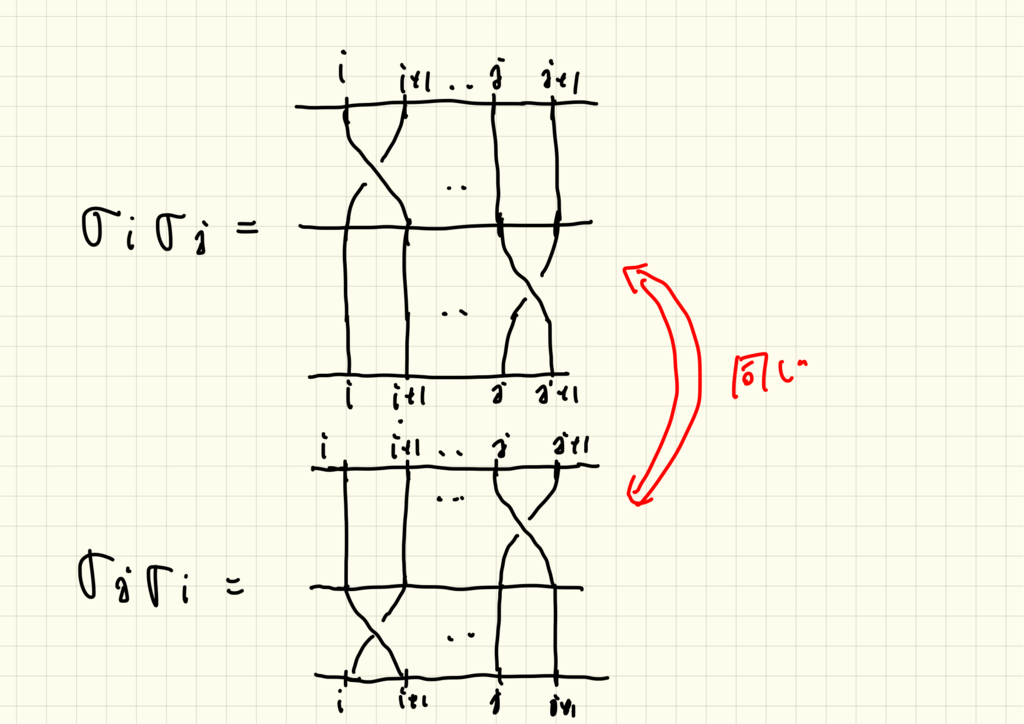
ブレイド群の交換子群
一般に群に対してその交換子群
は以下のように定義されます。
フレンケルの論文ではブレイド群の交換子群を
という記号で表しています。ブレイドが
の元であるか否かを視覚的に判定することができます。
ブレイドの各交わり点について、左の紐が右の紐の上を交差する場合に、そうでない場合に
を対応させます。その総和(交わり数と呼ぶ)をとったものが
であることと、そのブレイドが
の元であること、は同値になります。
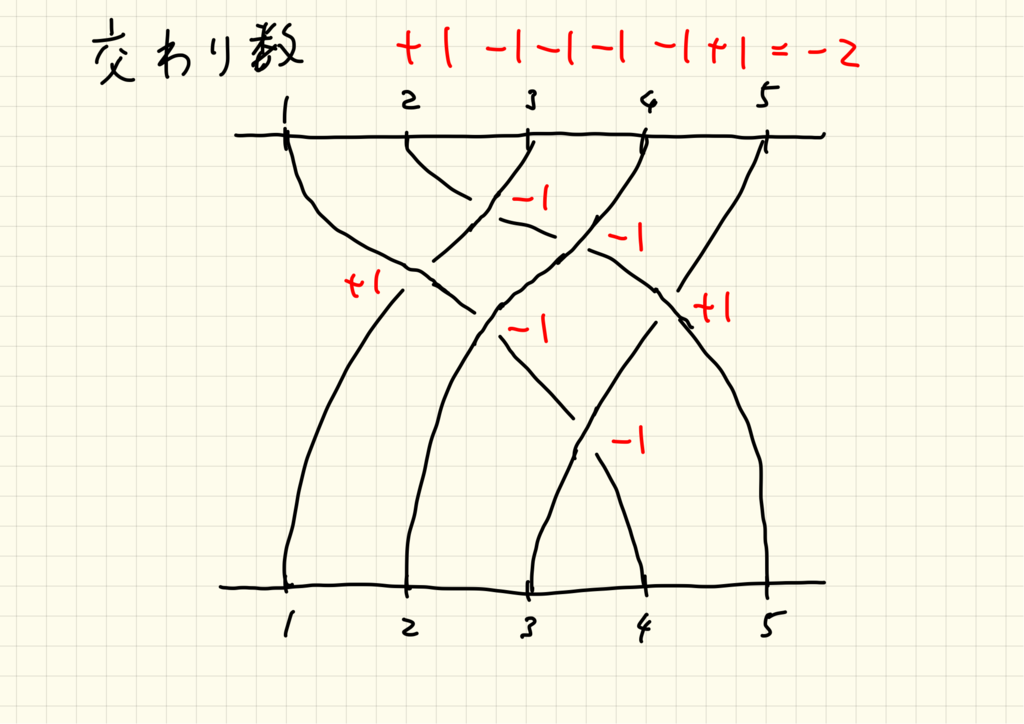
「は左の紐がその右の紐の上を通って交差する」、「
は左の紐がその右の紐の下を通って交差する」と見なせること、また
であることから
は
で定義される準同型(
)の
ではないかと予想されるのですが、それは実際正しいです。
ということでを示したいと思います。
という事でがどのような群かがわかりました。
 の基本群が
の基本群が になること
になること
は複素平面上の相異なる
個の点からなる空間とみなせました。複素平面を板、相異なる
個の複素数をくぎとみなすことで、
内の閉路はブレイドと同一視できます。閉路は通常
というパラメータで表せるため、
に対応するのが上の板、
に対応するのが下の板と考えます。閉路であるため上の板と下の板のくぎは全く同じところに刺さっています。

ひもは各複素数の点がどう移動するかを表します。紐が1点で交わることはありません。もし交わってしまうと二つの点が同じ複素数になってしまい、判別式が0になってしまうからです。
閉路の連続変形は紐をくぎから外すことなく行う事の出来る変形に対応します。そう考えるとの基本群が
になりそうな気がしますね*8。
 の基本群が
の基本群が になること
になること
上の閉路は
個の点(多項式の解)を互いに重ならない限り自由に動かすことができました。つまり対応するブレイドの紐も好きなように動かせたのですが、
は多項式の判別式の値が
であるという強い制約があるため、
個の点を自由に動かすことができません。
個の点を決めると残りの
個の点の候補は限られます。
閉路ではどの点も連続的に動く必要があります。そのことを考慮すると、出発点となる個の点を決めたとき、各
で
個の点を決めると残りの
個の点の位置は一意に決まります。ブレイドで考えると
本の紐を自由に絡ませたときに、残りの
本の紐の動きは一意に決まってしまい、最終的に完成するブレイドの交わり数は
になります。つまり基本群が
になるのです。ただこれについては全く証明ができず、数値実験するにとどまりました。今後の勉強でしっかり証明したいです。
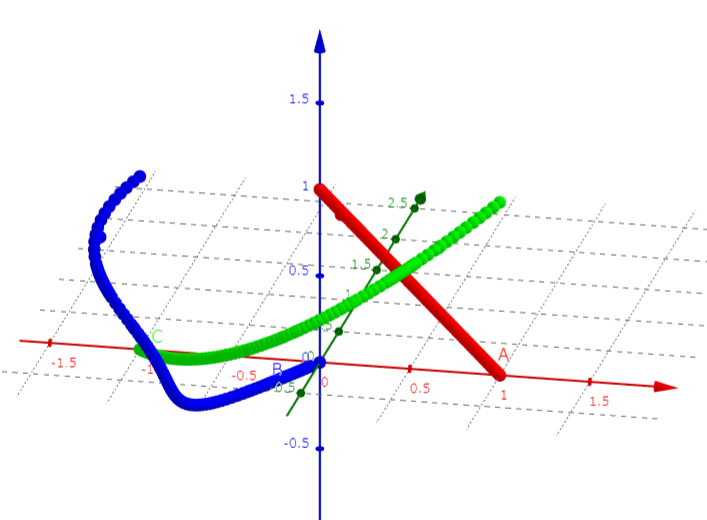
数値実験の例です。、
、
を解とする方程式
に対して、私が人為的に
を
に動かす赤い紐、
を
に動かす緑の紐を作り、判別式一定の条件で決まる青の紐を計算して可視化しました。
つめはちょっと難しいですが交わり数が
になっていることがわかります。

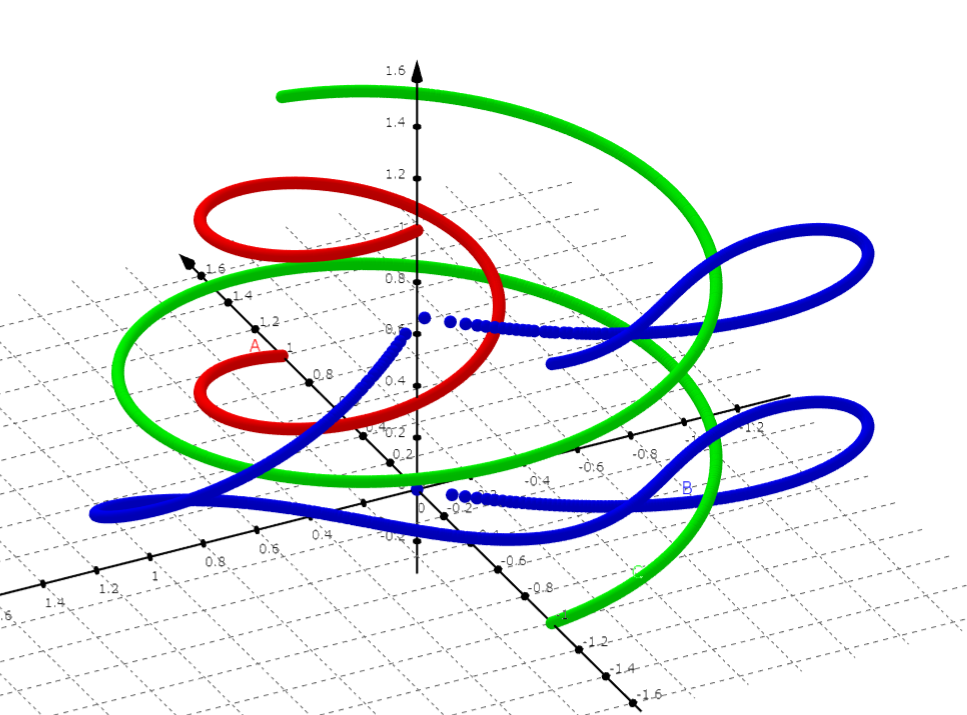
違ったアングルからの写真も面白いです。
続き頑張ります!
*1:遅くても来年中には終わらせたいですが、数学は果てしないので約束はできません。ただやるといったらやります
*2:「なぜ分類したいのか?」となぜなぜを続けるといつまで経っても終わらないので、ここは出発点とさせていただきます。
*3:と対応させることで
*4:今後ちゃんと示すかもしれません。
*5:何度も書きますが、間違っている可能性もあります。今後の勉強で発覚した場合は都度履歴が分かるように訂正していきます。ご了承ください。
*6:現時点では証明ができていません
*7:紐の収縮や、板と板の間の距離の違い、紐をくぎから外すことなく互いに変形できる結び目は同一視します。
*8:こういった定性的な話をいかに数式で厳密に証明するのかは今後の自分の課題です。