麻雀×プログラミング×数学
はじめに
東京では今年から「伝道師になろう」というイベントが定期的に開催されています。伝道師になろうってなんだろう?」という方は、狐さんの下記の記事を参照してください。
簡単に言えば「自分の好きなことを、知らない人にもわかりやすく、なぜ好きかを伝えて、面白さを伝道しよう」という企画です。僕も参加したことがあります*1。
コンセプトが本当に素晴らしいので、来年はこのイベントが全国に広がればいいですね。狐さんによると、ビブリオバトルのように誰が始めたかわからないくらいとのことです。
数学以外に好きなもの
僕が好きなものは絶対的に数学です。伝道できる(と自分で思っている)ものは数学しかありません。しかし、伝道師になろうは日曜数学会から派生したイベントということもあって、このアドベントカレンダーに数学ネタだけを書くのは少し気が引けます*2。
僕は数学以外で好きなものを聞かれると「麻雀」、「プログラミング」、「京都」、「熊野寮」、「料理(←最近やっていない)」、「小籠包」、「ヒカルの碁」から選出して答えていますが、数学とこれらには、好きレベルでいうと、
数学>>>>>>|超えられない壁|>>>>>>麻雀、プログラミング、京都、熊野寮、料理、小籠包、ヒカルの碁(順不同)
くらいの差があります。数学に関しては永遠に熱く語る自信がありますが、その他の好きなものは最高でも3時間程度しか語れない気がします。ただその他の好きなものも数学とコラボさせることでそれなりのボリューム、ネタになるのではないかと思い、今回「麻雀」、「プログラミング」を選抜して、投稿しました。
まず最初に、伝道師になろうのルールに則って、「麻雀」、「プログラミング」、「数学」がそれぞれなぜ好きなのかを語っていくことにしましょう。
麻雀が好きな理由 (半分は熊野寮の話)
麻雀が好きな理由を2点挙げます。
まず1点目は運の流れを感じることができる、そして運がいい時は最高に気持ちがいいということです。
普段生活の中で運がいいとか、悪いとかを考えることは少なくなってきましたが、麻雀をやっていると何をやってもうまくいく無双状態というものを体感できます。とにかく配牌(最初に配られる牌)がいい、とにかくいい牌をツモる(牌を引くこと)、そしてとにかく点数が高い状態です。まさに下記の女子プロの豊後さんのような状況です。
無双状態は滅多に発生するものではありませんが(感覚的には5半荘に一回)、無双状態になった時の快感を味わうために麻雀をやっていると言っても過言ではない気がするくらい楽しく気持ちいいです。
2点目は仲間と語り合いながらやるとやっぱり楽しい、というところです。
(ここからは熊野寮の話を交えつつ説明していきます。)
僕が麻雀を覚えたのは大学生時代の時です。先に挙げた数学以外の好きなものの中に「熊野寮」というものがありましたが、僕は学生時代に熊野寮に6年間住んでいて、そこで先輩に麻雀を教わりました。熊野寮は古いですが最高の寮です。素数大富豪の大会が開催された最初の場所でもあり、最近のトレンドをいち早く吸収するあたりはさすがと思います。Googleで"熊野寮"を画像検索するとその凄さをわかっていただけると思いますので、是非調べてみてください。なお、家賃は700円です。ただ電気代や食堂のお姉さんたちの保険料等が追加され、実際は4,100円でした。それでも安い!
熊野寮にはA棟、B棟、C棟があり、それぞれ各階に談話室があります。僕はA棟3FのA3談話室に住んでいました。これは談話室に入り浸っていたという比喩的な表現ではなく、談話室の片隅に本棚で人一人分寝れるスペースを作って、そこに住んでいました。談話室には大学生の娯楽が詰まっています。ゲーム、漫画、お酒、麻雀。。。みんな好きな時に談話室に来て、好きなことをして語り合っていました。今思っても楽しい空間です。そして下記理由から麻雀こそ仲間との語り合いにピッタリな遊び、ゲームだと思うのです。
- 手を動かすだけで疲れないから長時間できる
- ご飯食べながらでもできるから長時間できる
- 時々「ポン、チー、ロン、ツモ」という以外は発声の必要がないいからお話しができる
実際、談話室でやる麻雀は娯楽でやる麻雀ですので、いつも楽しく語り合っていました。朝まで仲間*3と語りながら麻雀をやることも珍しくなかった僕としては、麻雀は語り合いのゲームで楽しいんだ!ということを伝道したいと思います*4。
女子用の雀荘(タバコは絶対禁止、フードメニューにスイーツ、カクテル多め)とか作れば、女子会にピッタリな気がしますね。
では麻雀が好きな理由はこれくらいにして、先に進みましょう。
プログラミングが好きな理由
これに関しては、数学の計算ができるからという一言に尽きます。コンピュータというのは和訳すると「計算機」ですし、プログラミングはコンピュータに命令を与えるものですので、「計算機に命令を与えるもの」がなぜ好きかと聞かれて、「計算ができるから」と答えてるだけになります。何の回答にもなっていないように思えますが、その言葉以上に計算できることは素晴らしいと思うのです。
例えば、あなたがお望みであれば僕は4,294,967,297や147,573,952,589,676,412,927が素数でないことをプログラミングで簡単に示すことができますが、一昔前はそれは大変難しいものでした。
4,294,967,297に関してはtsujimotterさんの下記の記事を、
tsujimotter.hatenablog.com
147,573,952,589,676,412,927に関しては、下記のフランク・ネルソン・コールの逸話をご参照ください。
メルセンヌ数 - Wikipedia
上記の記事にあるように、昔の人は20桁程度の素因数分解ですら難しかったのです*5。円周率の計算に一生を費やした人がいます。そして死後に誤りを指摘されてしまった悲しい人もいます。その人達が一生を費やして計算した円周率の値は、おそらく僕は30分程度プログラミングをすると手に入れることができます。
17世紀のケプラーはブラーエが残した大量の観測データから、地球が楕円軌道で太陽の周りを回っていることを突き止めました。また、18世紀のオイラーがが
と予想したのも*6、19世紀にガウスが小惑星ケレスを発見できたのも全部大量の計算の賜物でしょう。
僕自身も前回のブログで書いた素数大富豪の会心の一撃のシミュレーションは、プログラミングをしなければ一生かかっても終わらなかったでしょうし(というか絶対途中でやめる)、プログラミングをせずにゼータ関数の零点を計算するのがいかに大変であるかを経験したこともあります。
ネイピアが対数を発見するために引きこもった強い動機となったように、昔の人の計算との戦いは想像を絶するものだったと思います。もしオイラーやガウスにプログラミングを教えてあげれば、二人は泣いて喜ぶのではないでしょうか*7。プログラミングをすることでそのような計算をいとも簡単に行うことができる。直接的な理由ですが、これがプログラミングを好きな理由です。
数学が好きな理由
これは語ると切りがありませんし、語り切れるとも思えません。そしてまだまだ自分でもなぜ好きがかわからない状況です。ちょうど半年くらい前に自分がなぜ数学が好きなのかをマインドマップで殴り書きしていました。狂気じみていますが、こちらを貼り付けることで好きな理由に代えさせていただきます。
ついでに同じタイミングで数学ってどんな分野があるかも殴り書きしていました。

どちらも何も見ずに5分くらいで書き上げたものです。汚い字で読めないですが、それだけ好きなんです、
ただ、これじゃ全然伝道していないので、1点だけ言わせてください。(ここから先はあくまで持論です。)
「数学は紙とペンがあればどこでもできる*8」ということを好きな理由として強調したいです。これは「紙とペンがあれば計算できるしね」みたいな単純な話ではありません。数学的実体なんてこの世のどこにも存在しません。 虚数はその名の通り現実に存在しないような名前が不本意に与えられていますが、実数の1という数はどこに存在していますか?紀元前にピタゴラスによってピタゴラスの定理が発見されましたが、ピタゴラス以前にもピタゴラスの定理は成り立っていたはずです。ピタゴラスの定理はどこにあったのでしょうか?
1もピタゴラスの定理もこの世界のどこにも存在しません。でもこの世界のどこにでも存在しているのです。そして紙とペンを使うことでその数学的実体の化身が目の前に現れ、時代、人種、性別、年齢を超えて他の人とも寸分違わず同じものを認識しあえるのです。それは本当に奇跡のようなことだと思います*9。こんな奇跡を体感できるなんて。。。はぁはぁ。。数学ってすごいですよね。
この話はエドワード・フレンケルさんの「数学の大統一に挑む」から影響を受けていると思います。

- 作者:エドワード・フレンケル
- 発売日: 2015/07/13
- メディア: 単行本
また、日曜数学者の始祖であるtsujimotterさんも過去にtwitterで「旅行に行っている暇がない。今は数学的世界を探索するのに忙しい。」のようなことをつぶやいておられました。過去のツイートなので探しきれませんでした。まさに同感で、僕らは紙とペンを使うことで、この世界よりもずっと広大な数学的世界を探検できるのです。。。はぁはぁ。。数学ってすごいですよね。
いよいよコラボ まずは麻雀の基本説明
なぜ好きかの説明が終わりました。「麻雀」×「プログラミング」×「数学」のコラボをしたいと思います。
そのためには最低限麻雀のことを知る必要がありますので、説明します。
まずは麻雀牌にどのようなものがあるかを説明します。麻雀牌は大きく数牌と字牌に分かれるのですが、この後の考察に字牌は不要ですので、数牌だけを考えます。数牌には萬子(マンズ)、筒子(ピンズ)、索子(ソーズ)の3種類があり(これを色と言います)、それぞれ1から9の数字が書かれています。色と数字が同じである牌はそれぞれ4枚あります。つまり数牌は3(色)×9(数字)×4=108枚存在します。

次にアガリの形を説明します。麻雀は14枚の牌を「3枚1組のグループ4つ」と「2枚1組の雀頭(ジャントウ)1つ」の形にすることでアガることができます。「3枚1組」は全く同じ牌3枚でもいいですし、同じ種類の牌で2,3,4のように3つの連続する整数の組でも良いです。雀頭は全く同じ牌の2枚組になります。
下記がアガリの形の例になります。
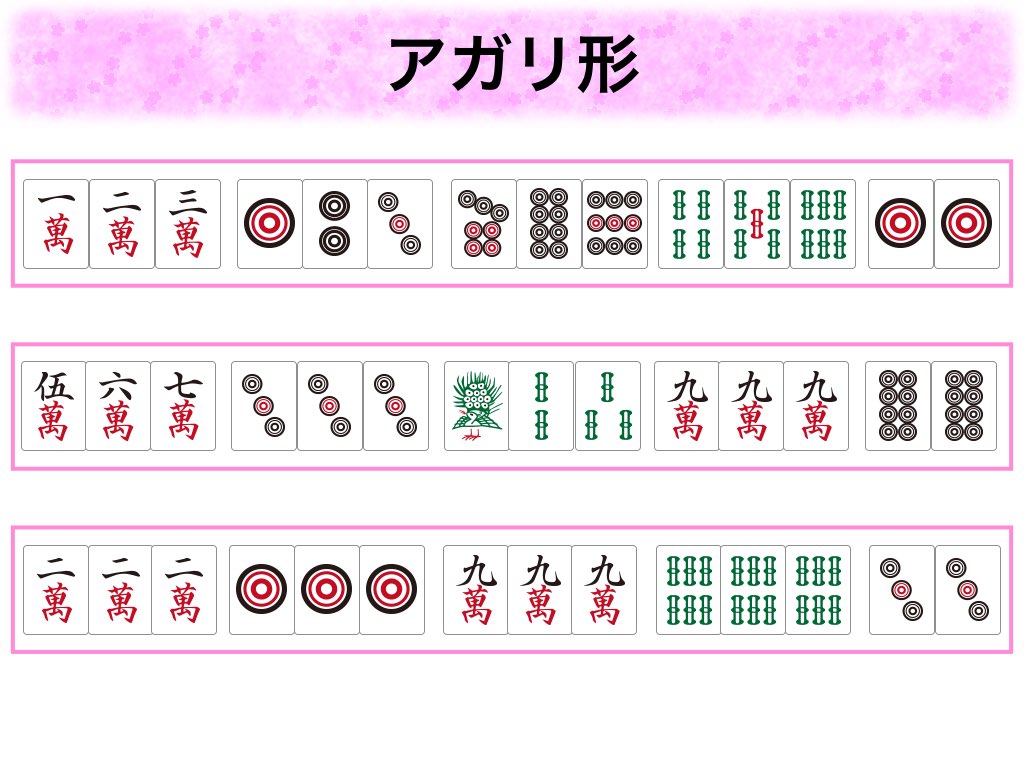
麻雀は基本的には手持ちの牌は13枚になっています。13枚の状態で1枚牌を引いて、14枚の状態になった時に、アガリの形になっていればアガることができます。アガれない場合は1枚引いたので、手持ちの14枚の牌どれでもいいので1枚捨てて再び13枚の状態にします。このようにアガリの形になるまで牌を交換し続けるゲームになります。アガリの形が特定の条件を満たせば役というものが付きます。役が珍しいものであればあるほどアガった時にもらえる点数が多くなります。
最後に、待ち牌について説明します。次に良い牌を引けばアガれる状態のことをテンパイしているといいます。テンパイしている時に引くことでアガれる牌、つまりアガるために待っている牌を待ち牌といいます。下記の例のように待ち牌は1種類とは限りません。


いろんなパターンの待ち牌がありますね。
以上で麻雀の基本説明を終わります。
第二の九蓮宝燈探索
唐突ですが、13枚の手持ちの牌が次の形の時、1〜9の牌全てが待ち牌になります。つまり1〜9のどの数牌を引いてもアガることができます。

実際に確かめてみると、確かにアガリの形になっています。



なお、この形でアガると九蓮宝燈(チューレンポートウ)という役の中でも特別な役満という役になります。九蓮宝燈はアガったら死んでしまうという迷信があるくらい珍しい役になっております。
「1〜9のどの牌がきてもアガれるなんて九蓮宝燈はすごいなあ。」と思うところですが、知られていないだけで、他にも1〜9のどれがきてもアガれる13枚の手牌が存在するも知れません。そんな未だ日の目を見ない第二の九蓮宝燈を見つけてあげたい、見つかったら僕だけでもそいつのことを役満と呼んであげたい。しかし、麻雀の手牌の組み合わせはそれなりに大きい数になりそうだし、それぞれの手牌でちゃんと待ち牌を漏れなく見つけられるか不安。。。。。
そんな悩みを解決するのがプログラミングなんです!
コンピュータはプログラミングした通りに高速に、嫌とも言わず、間違うことなく動いてくれます。正しくプログラミングすれば正しい結果が得られます。今回はどのようにプログラミングしたかの紹介はしませんが*10、実際にプログラミングして実験した結果、九蓮宝燈以外には1〜9の全てが待ち牌になるような手牌は存在しませんでした。
第二の九蓮宝燈が見つからなかったのは悲しいですが、それだけ九蓮宝燈はすごいものなんだ!ということがわかりました!
「プログラミングって強力だなあ。家に麻雀牌なくてもこういうことがわかるんだからなあ。」と思います。
一定の成果を得ましたが、まだ「麻雀」×「プログラミング」止まりです。
数学的に意味がある待ち牌
さて、プログラミングによって色々な手牌の待ち牌を調べられるようになりました。では最後に数学的エッセンスを加えて本記事を締めくくりましょう。
スライドを見ていただければ、説明は不要です。なお、不思議なことに下記の4種類すべてちょうど2パターンずつでした。

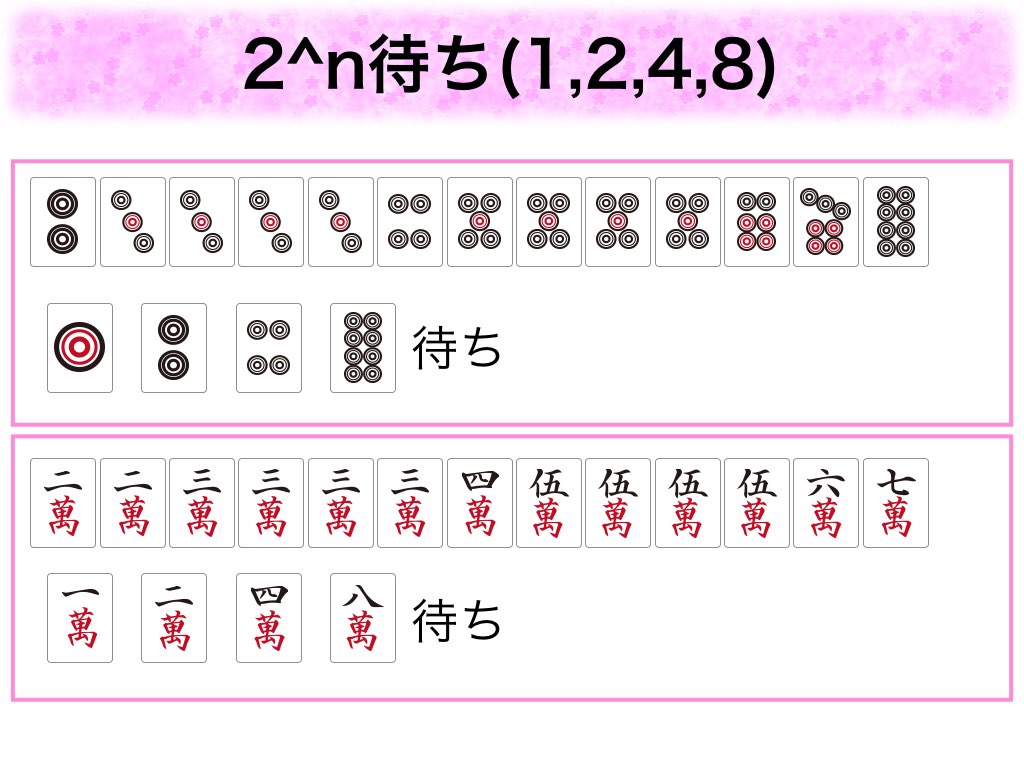

最後はみんな大好き素数です!

明日はHaru Negamiさんの「好きすぎて食べちゃいたい◯◯」です(^_^)
ありがとうございました。
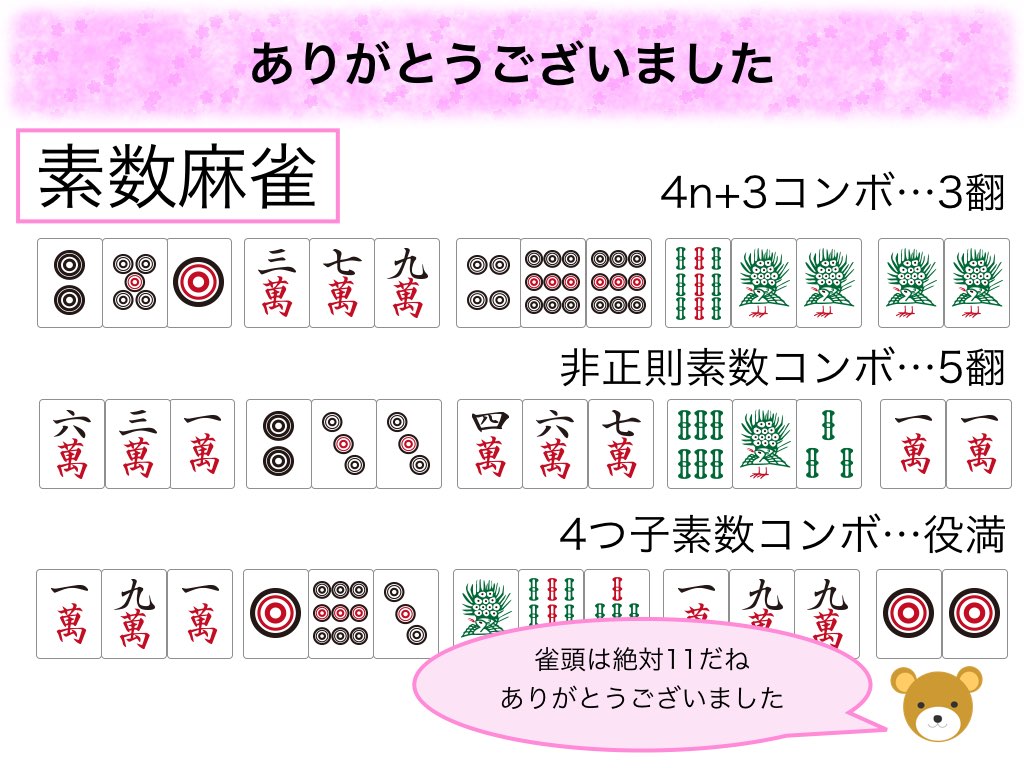
*1:今回は学生時代の話をするため、一人称は「僕」を使いたい気分です。
*2:数学に限らず好きなものをどんどん発表していこう!というのが元々の誕生理由な気がするため。
*3:熊野寮のメンバーは家族でも友達でもない仲間という表現がよく当てはまる気がします。
*4:しかし熊野寮のような特殊な環境はほとんどありません。誰かのアパートで麻雀しても多分隣の部屋の人からうるさいと怒られるでしょう。雀荘に行ったらお金がかかります。仲間が集い会えるような場所が欲しいところです。
*5:本質的には今も難しいです。RSA暗号の基本原理です。でもそれはまた別のお話。
*7:しかし、この二人は数学界の偉人中の偉人で常任にはその底は計り知れないので、コンピュータどころでは泣いて喜ばない気もします。オイラーは人が呼吸をするように、鳥が空を飛ぶように計算していたと言われています。
*8:実際は教科書も欲しいところ。
*9:かなりスピリチュアルなことを言っていますが、哲学的な話は大の苦手です
*10:汚いソースを見られるのは超恥ずかしいため。