蔵本予想とは何か? 〜予想紹介編〜

1/7に第8回日曜数学会にて「蔵本予想とは何か?」というタイトルで力学系理論に関するLTをさせていただきましたのでご紹介します。私の不勉強のため今回は蔵本予想の紹介に留まりましたが、近いうちに証明も体得して概説したいと思い、本記事では〜予想紹介編〜というサブタイトルを付けております。

f:id:mattyuu:20170108202050j:plain

蔵本予想とは同期現象に関する数学的な予想になります。"予想"と書いていますが、九州大学の千葉逸人准教授によって証明されています。今回は蔵本予想の概説を行いたいと思います(不勉強ゆえ間違った記載があるかもしれません。あくまでざっくり蔵本予想がどういうものなのかを知っていただければと思います。)。

f:id:mattyuu:20170108202111j:plain

まず同期現象とは何かを説明します。多数の蛍が集まっている場面、または、多数のメトロノームを集めた状況(←台車の上に置く等、相互に作用するようにする。固い台の上においてはダメ。)を想像してください。最初はそれぞれの蛍が各々のタイミングで発光し、メトロノームが各々のペースで針が振れているのに、十分な時間が経つとまるで一匹の蛍のように、まるで1つのメトロノームのように発光のタイミング、針の触れ方、ペースが揃ってくることが観測されます。これを同期現象といいます。

youtubeに蛍の美しい同期現象がありましたので、リンクを貼っておきます(開始35秒くらいから同期現象の動画が始まります。)。

www.youtube.com

f:id:mattyuu:20170108202123j:plain

こういった同期現象を語る数学的なモデルに蔵本モデルがあります。これは京都大学の蔵本由紀教授により提案されたものです。

蔵本モデルは上記のような微分方程式で表されます。3ステップでこの式が意味するところを解説したいと思います。

f:id:mattyuu:20170108202137j:plain

まずステップ1です。蛍の点滅やメトロノームの針が左右に振れる運動のように、同期現象の元となる単体の運動は周期的な運動です。周期的な運動ということで、質点が一定速度で円周上を回る運動をモデルの出発点としましょう。

このモデルの運動を記述する変数として質点が円周の中心となす角 $\theta$ をとります。 $\theta$ は時間 $t$ の経過と共に変化していきますので、変数 $\theta$ はまた時間 $t$ の関数とも思えます。その意味で $\theta$ を $\theta(t)$ とも書きます。

次に回るスピード(自然振動数と呼びます。単位時間当たりどれだけの角度回るかという値です。)を $\omega$ とすると、このモデルを記述する微分方程式は、

$\displaystyle \frac{{\rm d}\theta}{{\rm d}t}=\omega$

となります。

自然振動数 $\omega$ が大きければ大きいほど質点が円周を回るスピードが速くなっていきます。 $\omega$ は固体によって異なる値を取り得ます。例えば短い間隔で点滅を繰り返すせっかちな蛍の $\omega$ は大きく、長時間かけて点滅を繰り返すのんびり屋の蛍の $\omega$ は(絶対値が)小さくなります。

この微分方程式は簡単に解けて下記のように表せますが、力学系理論ではシステム(系)の状態を微分方程式で表すことが通常ですので、次のスライド以降も微分方程式の形で進めていきます。

$\displaystyle \theta(t)=\omega t + \theta_o$

ステップ1では1つの質点の円周上の運動を考えましたが、質点が1つでは同期現象を考えようがありません。では、次のステップに進みます。

f:id:mattyuu:20170108202151j:plain

ステップ2では同期現象を発生させるために質点をたくさん、ここでは $N$ 個集めます。

質点をN個に変更することに伴い、変数 $\theta$ も増やす必要がありますので、添え字 $i$ を付けて $\theta_i$ $(i=1,2,\cdots,N)$ とします。そして自然振動数も固体によって異なってもよいものでしたので、変数 $\theta_i$ に対応する自然振動数も $\omega_i$ のように添え字を付けて表します。

ステップ2で質点の数を $N$ 個に増やしましたが、 $\theta_i$ の運動を定める微分方程式には $\theta_i$ の運動の自然振動数 $\omega_i$ しか出てこず、 $\theta_j$ $(j\neq i)$ は登場しません。つまりそれぞれの質点は自分のペース(自然振動数 $\omega_i$ )で回り続けるだけであり、まだ同期現象は発生しません。では、次のステップに進みます。

f:id:mattyuu:20170108202205j:plain

ステップ3では質点の運動を定める微分方程式に上図の項を加えます。 $\theta_i$ の運動を決める微分方程式に $\theta_1$ から $\theta_N$ が登場することで、初めて変数間の相互作用が発生します。これで蔵本モデルの完成です。

この相互作用項の主要な部分は $\sin{(\theta_j-\theta_i)}$ になります。

$\theta_i$ の微分方程式の右辺の相互作用項を考察していることに注意して、 $\theta_j$ $(j\neq i)$ が $\theta_i$ より少しだけ大きい場合*1、 $\sin{(\theta_j-\theta_i)}$ は正になりますので、 $\theta_i$ は $\theta_j$ から回るスピードが速くなるように相互作用を受けます。

逆に $\theta_j$ が $\theta_i$ より少しだけ小さい場合は、 $\theta_i$ は $\theta_j$ から回るスピードが小さくなるように相互作用を受けます。

$\sin{(\theta_j-\theta_i)}$ という相互作用により $\theta_i$ さんと $\theta_j$ さんがお互いにお近づきになりたい気持ちがあるということがわかっていただけると思います。実際は $\theta_1$ から $\theta_N$ 全てから相互作用を受けるので、 $\theta_j$ だけの相互作用を考えるだけでは、回るスピードが速くなるのか遅くなるのかはわかりません。

$\sin{(\theta_j-\theta_i)}$ は $\sum_j$ で和を取っています。質点の個数 $N$ が大きくなっても相互作用項が大きくなり過ぎないように相互作用項の分母に $N$ が入っています。

また、 $K$ は相互作用項の大きさを決めるパラメータになります。この $K$ が大きければ大きいほど同期現象が起こりやすくなります。つまり $K$ は、(次スライドに続く)

f:id:mattyuu:20170108202228j:plain

つまり $K$ は、空気(Kuki)を読む力です。

図のように $\theta_j$ さんに比べて少しだけ遅れている $\theta_i$ さんは $\theta_j$ さんにおいて行かれないように頑張って速く回ろうとします。逆に $\theta_j$ さんは $\theta_i$ さんが遅れていることに気づいて、ペースを落としてあげようとします。

このように空気を読んで相手を思いやる力の大きさ、それが $K$ なのです。

$K$ を大きくするに従って、同期が発生しやすくなる。これが蔵本予想の要となります。

f:id:mattyuu:20170108211232j:plain

ここで、同期の発生具合を定量的に把握するための指標を定義しておきます。

$N$ 個の質点が半径1の円周上を運動している時に、 $N$ 個の質点の重心*2と円の中心との距離 $r$ を同期具合と呼ぶことにします*3。

図では青い点が質点の重心となっています。全く同期が発生していない場合の同期具合 $r$ は $0$ ですが、同期現象が現れると同期具合 $r$ はだんだん $1$ に近づいていきます。

数式ばかり見ていてもイメージが湧かないので、空気を読む力 $K$ を大きくしていくと、同期具合 $r$ も大きくなっていくことを実際にシミュレーションをして確認したいと思います。そのためのモデルとしては、(次スライドに続く)

f:id:mattyuu:20170108202451j:plain

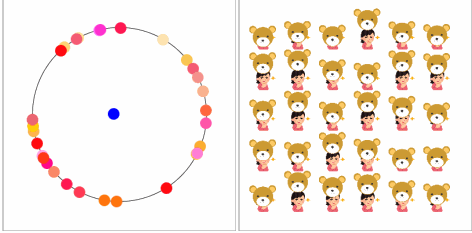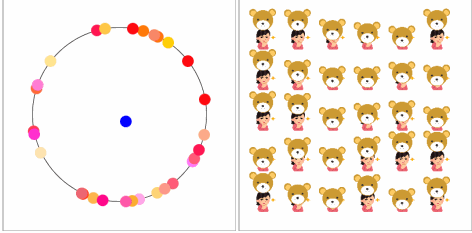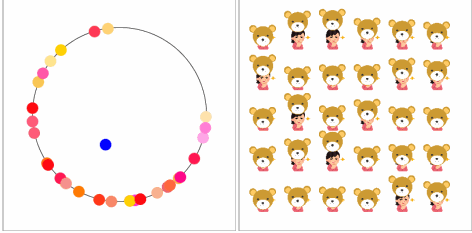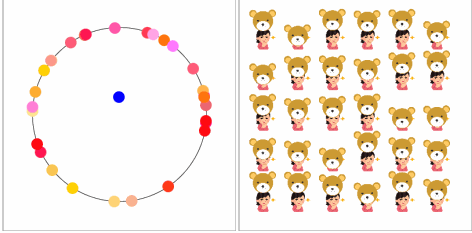
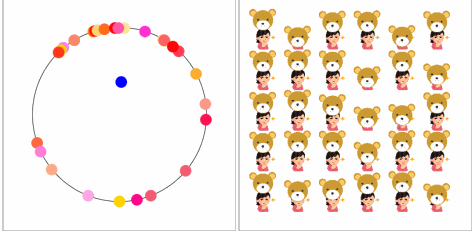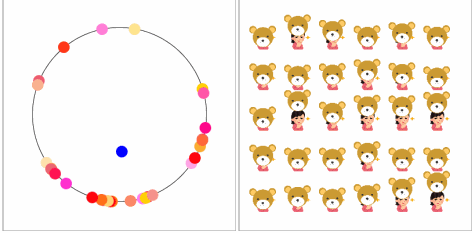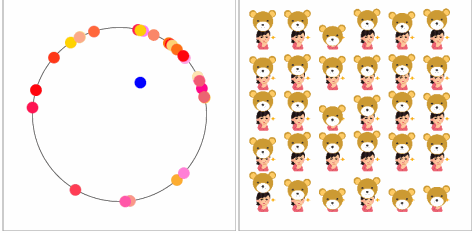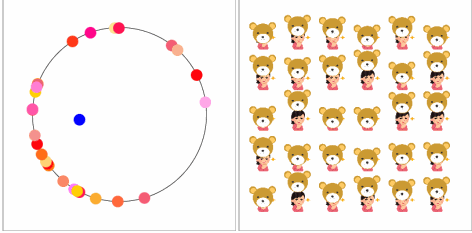
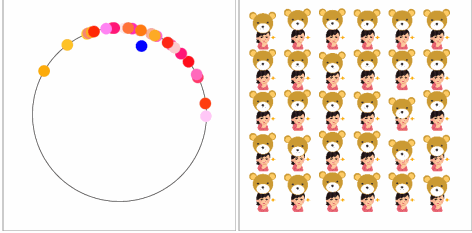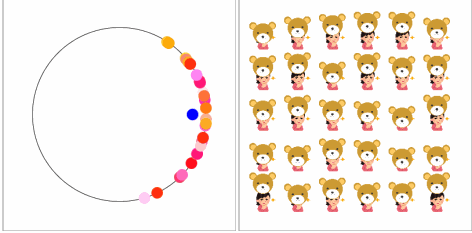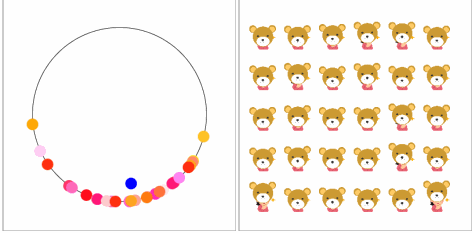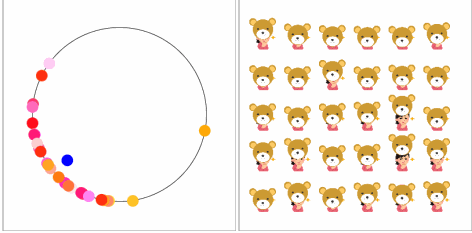
シミュレーションのモデルとしてはクマさんの着ぐるみのバイトの子を使いましょう*4。図のバイトの子はクマさんの被り物を一定のペースで付けたり外したりする趣味を持っています。そんなバイトの子を30人集めて、各々自分のペースで趣味を楽しんでもらいましょう。ただいつもと違うのは周りに同じ趣味を持つ子が29人いることです。空気を読む力 $K$ を大きくしていくと、どうなるでしょうか?

【空気を読む力 $K=0$ 】
みんな自分のペースで楽しんでいます。
f:id:mattyuu:20170108194310g:plain

【空気を読む力 $K=1$ 】
変わりはないように見えます。
f:id:mattyuu:20170108194359g:plain

【空気を読む力 $K=2$ 】
みんなのペース、タイミングが同じになってきています。
f:id:mattyuu:20170108194433g:plain

【空気を読む力 $K=10$ 】
何かのお遊戯会のように足並みが揃っています。
f:id:mattyuu:20170108194458g:plain

確かに $K$ を大きくしていくと同期具合が大きくなっていっていることがわかりますね。では最後に蔵本予想とは何かをざっくり説明します。

f:id:mattyuu:20170108202508j:plain

蔵本予想
$N\rightarrow \infty$ の極限で、空気を読む力 $K$ と同期具合 $r$ の関係は図のグラフのようになる。

ポイント1:
空気を読む力 $K$ が小さい間は同期具合 $r$ は0のまま。空気を読む力がある値 $K_c$ (←自然振動数の確率密度関数だけに依る値)を超えると、同期具合 $r$ が大きくなり始める。

ポイント2:
空気を読む力 $K$ が $K_c$ に近い時、同期具合 $r$ は $\sqrt{K-K_c}$ に比例する。

ポイント1のように状態の変化具合が $K_c$ を境に急に変わること(微分が不連続になること)を相転移といいます。固体が液体に、液体が気体になる現象と同じ定義です。みんなが多少空気を読んだところで全く同期が起きません。空気を読む力を上げていくと、急に同期が起こり始め「え？さっきまでみんな同期してなかったのに急にどうしたんだよ？」という状態になります。これが蔵本予想なのです。(先ほどのシミュレーションでは $K=1$ では同期が起きてなさそうでしたが、 $K=2$ では明らかに同期が発生していました。)

今回の記事はインターネットに公開されている千葉逸人准教授の下記論説の最初の2ページくらいを日曜数学会発表用に自分なりに解釈してまとめたものです。

http://www2.math.kyushu-u.ac.jp/~chiba/paper/sugaku2016.pdf

私の理解が至らず説明不足の点*5もありますし、解釈、説明が間違っている箇所もあるかもしれません。今後、何かの文献で証明を体得できたあかつきには、正しいステートメントで記事を書きたいです。まずは、「同期現象に関する蔵本予想というものがあって、それは空気を読む力と同期具合に関するものなんだ。そして、千葉逸人准教授が証明されたんだ。」ということを知っていただければ幸いです。

おまけ

今回行ったバイトの子のシミュレーションをするためのソースコードは下記になります。
ソースコードと言ってもただのhtml(javascriptも含みますが)なので、Internet ExplorerやSafariなどのブラウザがあれば自分のパソコンに閉じた世界で遊べます。(Safariでしか動作確認していません。ご了承ください。)

ソースの内容をkumamoto.html等の"html"拡張子でローカルに保存し、ダブルクリックで実行することで動かせます。(ただし、バイトの子と、クマさんの画像ファイルに代わる画像ファイルを何か2つ用意し、htmlファイルと同階層においてください。その後、ソース内の画像ファイル名を指定する箇所をそのファイル名で置換してください。)

<html lang="ja">
  <head>
    <meta charset="utf-8" />
    <title>Kuramoto Simulator</title>

    <!-- javascriptで実装する。 -->
    <script type="text/javascript">
      const NUM = 30; // 質点の数(変更してもいいが、バイトの子の描画は対応できていない。)
      const WIDTH = 400;  // 描画領域の横幅
      const HEIGHT = 400;  // 描画領域の縦幅
      var omega = new Array(NUM); // 自然振動数
      var theta = new Array(NUM); // 変数θ
      var theta_next = new Array(NUM);  // 次の時刻でのθを計算するための一時変数
      var r =  new Array(NUM);  // 質点の色を保持する変数 red
      var g =  new Array(NUM);  // 質点の色を保持する変数 green
      var b =  new Array(NUM);  // 質点の色を保持する変数 blue
      var ctx_circle;  // Canvasの2Dコンテキスト(使い方しかわかっていない)
      var ctx_kuma;

      var RAD = 150;  // 円周の半径
      var delta_t = 0.01; // 計算するときの1ステップの時間幅
      var K = 0.0;  // 空気を読む力 K

      var timer;  // startボタン、stopボタンで制御するためのタイマー変数(使い方しかわかっていない)

      var img_woman = new Image(); // バイトの子の画像
      var img_kuma = new Image(); // クマさんの画像


      // startボタンを押した時の処理
      // 一度止めて、Kの値を更新して再び動かす。
      function start(){
        clearInterval(timer);
        K = document.getElementById('K_VALUE').value;
        // 33msec間隔でdraw(描画)メソッドを呼び出す
        timer = setInterval(draw, 33);
      }

      // stopボタンを押した時の処理
      function stop(){
        clearInterval(timer);
      }

      // ネットで見つけた正規分布に従う乱数を発生させる関数
      /**
        * 正規分布乱数関数 参考:http://d.hatena.ne.jp/iroiro123/20111210/1323515616
        * @param number m 平均μ
        * @param number s 分散σ^2
        * @return number ランダムに生成された値
       */
      function seiki(m, s) {
        var a = 1 - Math.random();
        var b = 1 - Math.random();
        var c = Math.sqrt(-2 * Math.log(a));
        if(0.5 - Math.random() > 0) {
          return c * Math.sin(Math.PI * 2 * b) * s + m;
        }else{
          return c * Math.cos(Math.PI * 2 * b) * s + m;
        }
      }

      // 初期処理 htmlが読み込まれたタイミングで処理が走る
      function init(){
        // Canvasの2Dコンテキストの取得
        ctx_circle = document.getElementById('circle').getContext('2d');
        ctx_kuma = document.getElementById('kuma').getContext('2d');

        // 各質点の色、自然振動数、初期値の設定
        for(var i = 0; i < NUM; i++){
          
          // r,g,bいずれも乱数にすると見た目が良くないので、rは255に固定する。
          r[i] = 255;//Math.floor(Math.random() * 256);
          g[i] = Math.floor(Math.random() * 256);
          b[i] = Math.floor(Math.random() * 256);

          // 自然振動数は平均1、分散1になるように設定
          omega[i] = seiki(1.0,1.0);
          
          theta[i] = Math.random()*2*Math.PI;
        }

        // 画像ファイルの設定
        img_woman.src = "pose_kiri_woman.png"; // TODO なんでもいいので画像ファイルに差し替えてください
        img_kuma.src = "kuma.gif"; // TODO なんでもいいので自分が持っている画像ファイルに差し替えてください

        // 描画をスタートする。
        start();
      }

    // 描画メソッド(この中で微分方程式の差分の計算もしている。。。メイン部分) 
    function draw(){

      // 微分方程式の計算
      keisan();
      // 円周上の運動の描画
      draw_circle();
      // バイトの子の描画
      draw_kuma();
    }

    // 微分方程式の計算
    function keisan(){
      // 10ステップを計算する。1ステップごと描画していた遅々とアニメが進まなかったため。
      for(var l=0;l<10;l++){
        // 微分方程式の差分の計算部分
        for(var i = 0; i < NUM; i++){
          // 相互作用のsin部を足すための一時変数
          var sum_sin = 0.0;
          for(var j=0;j<NUM;j++){
            sum_sin += Math.sin(theta[j]-theta[i]);
          }
          theta_next[i] = theta[i] + (omega[i]+K*sum_sin/NUM)*delta_t;
        }
        // 次のθの値で現状のθを更新
        for(var i = 0; i < NUM; i++){
          theta[i] = theta_next[i];
        }
      }
    }

    // 円周上の運動の描画
    function draw_circle(){
      // 画面描画の更新仕様に関するおまじない
      ctx_circle.globalCompositeOperation = "source-over";
      ctx_circle.fillStyle = '#FFFFFF';
      ctx_circle.fillRect(0, 0, WIDTH, HEIGHT);

      // 円周の描画
      ctx_circle.beginPath();
      ctx_circle.fillStyle = '#000000';
      ctx_circle.arc(convertX(0), convertY(0), RAD, 0, Math.PI*2.0, true);
      ctx_circle.stroke();
 
      // 円周上の質点の描画部分
      for(var i = 0; i < NUM; i++){     
        //更新した座標で円を描く
        ctx_circle.beginPath();
        ctx_circle.fillStyle = 'rgb(' + r[i] + ',' + g[i] + ',' + b[i] + ')';
        ctx_circle.arc(convertX(Math.floor(RAD*Math.cos(theta[i]))), convertY(Math.floor(RAD*Math.sin(theta[i]))), 10, 0, Math.PI*2.0, true);
        ctx_circle.fill();
      }

      // 重心の描画部分 まず平均を出して、描画する。
      var heikinX = 0.0;
      var heikinY = 0.0;
      for(var i = 0; i < NUM; i++){
        heikinX += RAD*Math.cos(theta[i]);
        heikinY += RAD*Math.sin(theta[i]);
      }
      heikinX/=NUM;
      heikinY/=NUM;
      ctx_circle.beginPath();
      ctx_circle.fillStyle = '#0000FF'; // 色は青固定
      ctx_circle.arc(convertX(Math.floor(heikinX)), convertY(Math.floor(heikinY)), 10, 0, Math.PI*2.0, true);
      ctx_circle.fill();
    }

    // バイトの子の描画
    function draw_kuma(){

      // 画面描画の更新仕様に関するおまじない
      ctx_kuma.globalCompositeOperation = "source-over";
      ctx_kuma.fillStyle = '#FFFFFF';
      ctx_kuma.fillRect(0, 0, WIDTH, HEIGHT);

      for(var i=0;i<6;i++){
        for(var j=0;j<5;j++){
          ctx_kuma.drawImage(img_woman, convertX(-175+60*i), convertY(150-70*j),40,40);
          ctx_kuma.drawImage(img_kuma, convertX(-185+60*i), convertY(170-70*j+15*Math.sin(theta[i+6*j])),50,40);
        }
      }
    }

      // htmlの座標の考え方が画面左上を原点、画面右に向かってx軸、下に向かってy軸になっており、わかりにくい。
      // 画面描画の中心を原点、画面右にx軸、画面上にy軸を取る数学で通常使う座標系から
      // htmlの座標系へ変換する関数
      function convertX(x){
        return x+WIDTH/2;
      }
      function convertY(y){
        return -y+HEIGHT/2;
      }

    </script>

    <style type="text/css">
      canvas { background-color:#FFF; border: 1px solid #999; }
    </style>
  </head>

  <!-- 画面表示部分 -->
  <body onload="init();">
    <!-- 各種ボタン、Kの値を設定するテキストボックス -->
    <input type="button" value ="start" onclick="start()">
    <input type="button" value ="stop" onclick="stop()">
    <input type="button" value ="reset" onclick="init()">
    K=<input type="text" id="K_VALUE" value ="0">

    <!-- javascriptのCanvasという仕様で描画する。
        円周上の運動と、バイトの子の運動の2つ描画領域を作成する。
        ブラウザのウィンドウの大きさによらず横に並べたいのでtable内に作成する。-->
  　<table>
      <tr>
        <td>
          <!-- 制御を行うため"circle"というidを付けたCanvas部品 -->
          <canvas id="circle" width="400" height="400">
          </canvas>
        </td>
        <td>
          <!-- 制御を行うため"kuma"というidを付けたCanvas部品 -->
          <canvas id="kuma" width="400" height="400">
          </canvas>
        </td>
      </tr>
    </table>
</html>