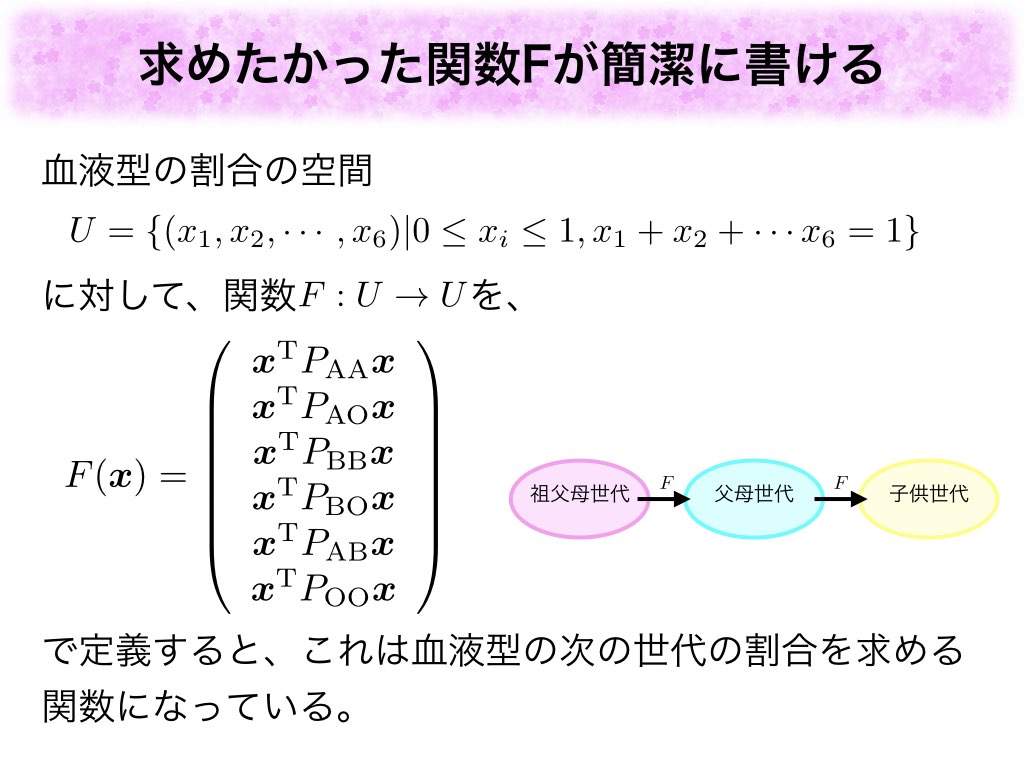
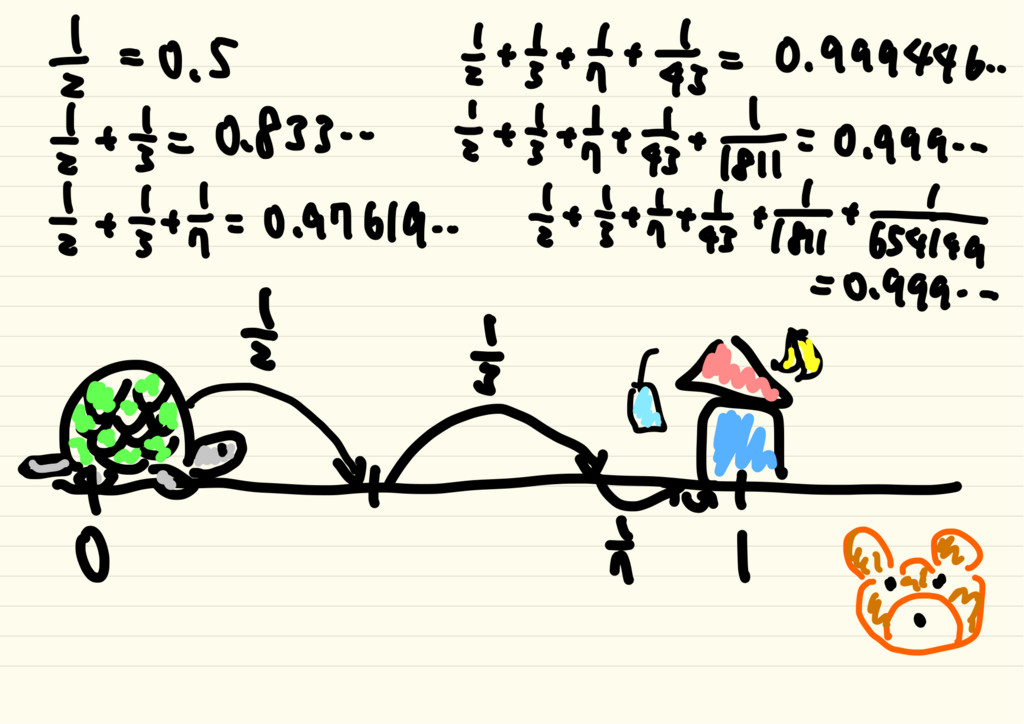10/20にマスパーティ内で行われたロマンティック数学ナイトプライム@ゼータ(以下、ロマ数ゼータ)に登壇させていただきました。マスパーティは30時間にわたって様々な数学の楽しみ方を紹介していくという数学イベントです。そんなぶっとんだイベントを成功させたマスパーティ主催のキグロさん、tsujimotterさん、ロマ数ゼータ主催のねげろんさん、司会のタカタ先生、その他スタッフ、登壇者の皆様に勝手に厚く御礼を申し上げます。
今回のロマ数ゼータはのことを知らない人からゼータの玄人の方まで楽しめるように、プレゼンを第1部、第2部、第3部にわけており、各部のコンセプトを下記のように定めていました。
私は第1部のトップバッターということで、ゼータ関数の歴史から、定義、魅力を一気に紹介しました。本記事では私がプレゼンした内容をほとんどそのままの形で掲載します。自分的にはほとんど数式を出していないつもりでいますので、、、数学が苦手な方も気楽に読んでみて下さい。本記事がゼータ関数に興味を持つきっかけになってもらえたら嬉しいです。
それでは、はじまり、はじまり

オイラーからの贈り物というタイトルで発表させていただきます。よろしくお願いします。

今回はロマンティック数学ナイトプライム@ゼータですが、ゼータを知らない方も多いと思いますので、ゼータが何者であるかわかるように紹介させていただきます。

ゼータ関数の名付け親は19世紀にドイツで活躍したリーマンです。リーマンは1859年の記念碑的論文「与えられた数より小さい素数の個数について」にて、というギリシャ文字でゼータ関数を書き表しました。この論文では、ゼータ関数を詳しく調べると素数の分布がわかるという驚くべき事実が証明されていました。またこの論文内のコメントから、有名なリーマン予想が誕生しています。
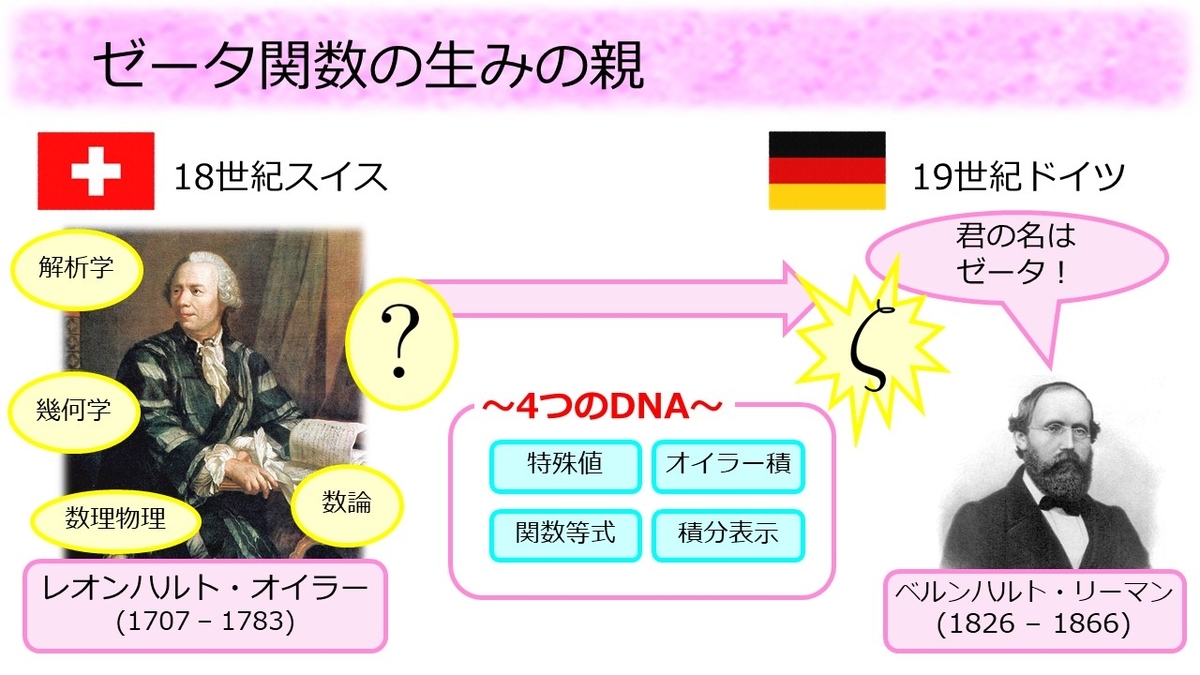
ゼータ関数の名付け親はリーマンですが、生みの親は18世紀にスイスで活躍したオイラーではないかと思います。オイラーは様々な分野で多大な業績を残す大数学者ですが、後の時代にゼータ関数と呼ばれる関数の研究も行っていました。その関数がリーマンによってゼータ関数と名付けられたことは先述のとおりですが、名もない関数がなぜ時代も国も違うリーマンの研究対象になったのでしょうか。それはオイラーが見つけたゼータ関数の性質がリーマンの琴線に触れたからに違いありません。このゼータ関数の性質を、「(ゼータの)4つのDNA」と勝手に名付け、1つずつ紹介していきます。

そもそもゼータ関数とは何でしょうか。ゼータ関数は"関数"です。関数とは数を入れたら数が出てくる装置です。例えば高校時代といった関数を習ったと思います。これは
を入れたら
が、
を入れたら
が出てくる関数であり、たしかに数を入れたら数が出てきています。ゼータ関数もただの関数なので難しく考える必要は全くありません。ゼータ関数が何者であるかは、数
を入れたときに、何が出てくるかがわかればよいことになります。
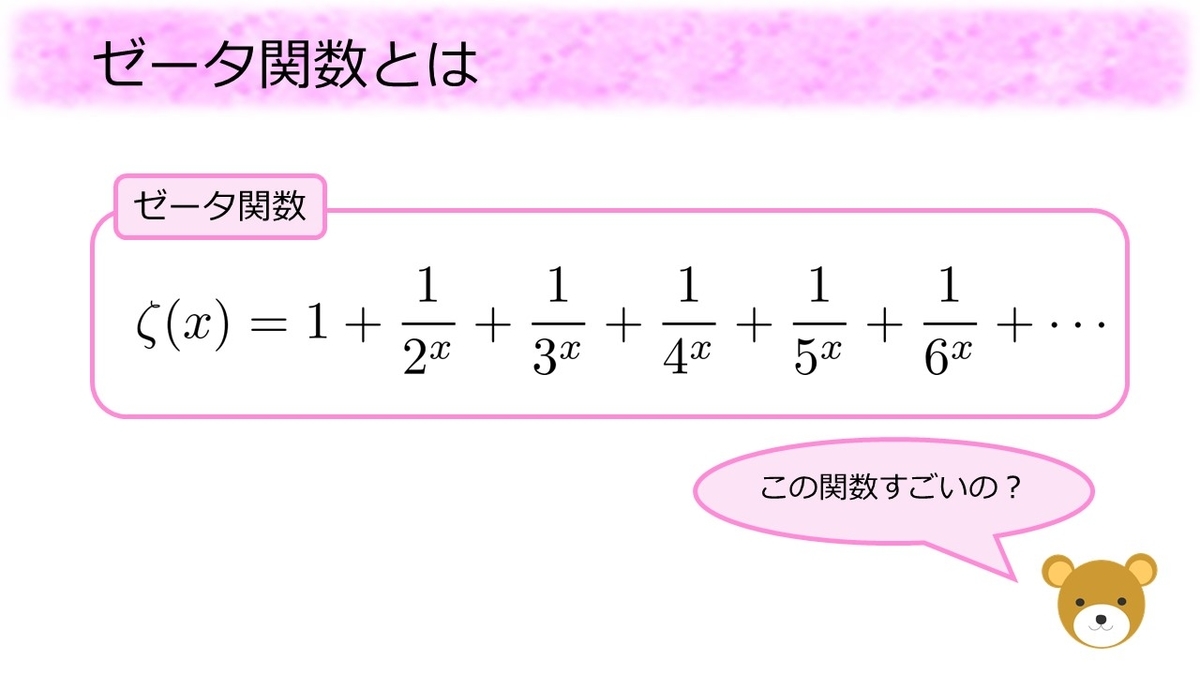
ゼータ関数は数を入れると、自然数の
乗分の1という形をした分数を、全ての自然数に渡って足し合わせた数を出す関数として定義されます。定義はいたってシンプルですが、このシンプルな関数がとても重要で、面白くて、愛すべき関数なのです。
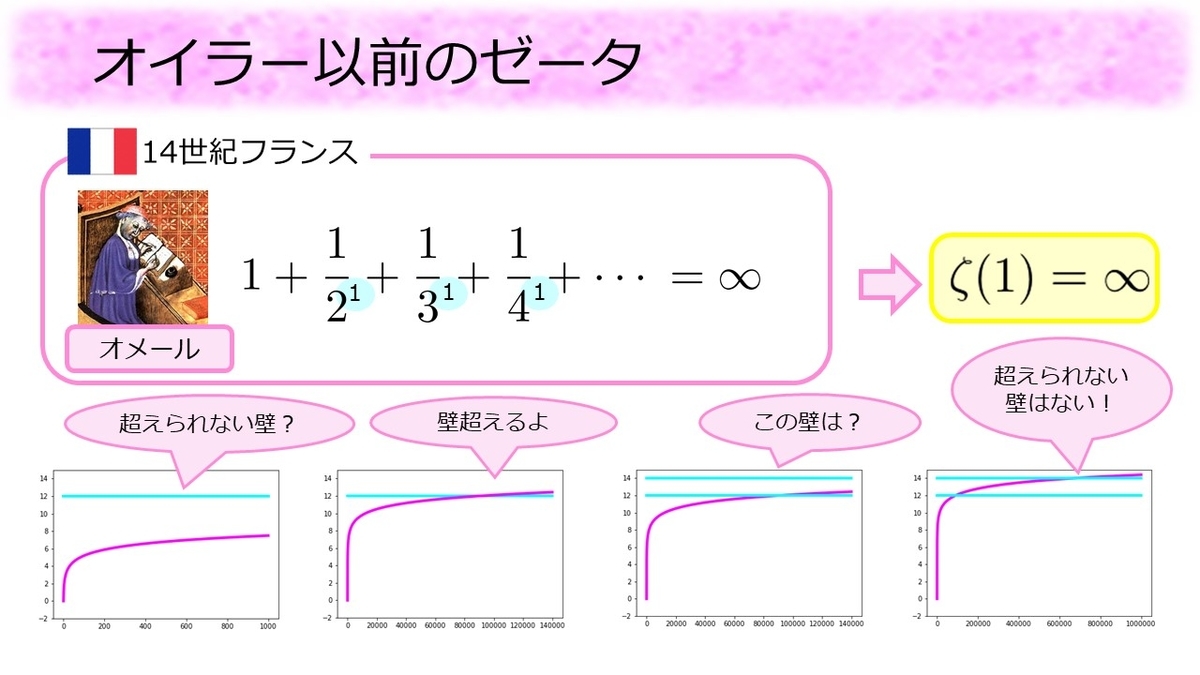
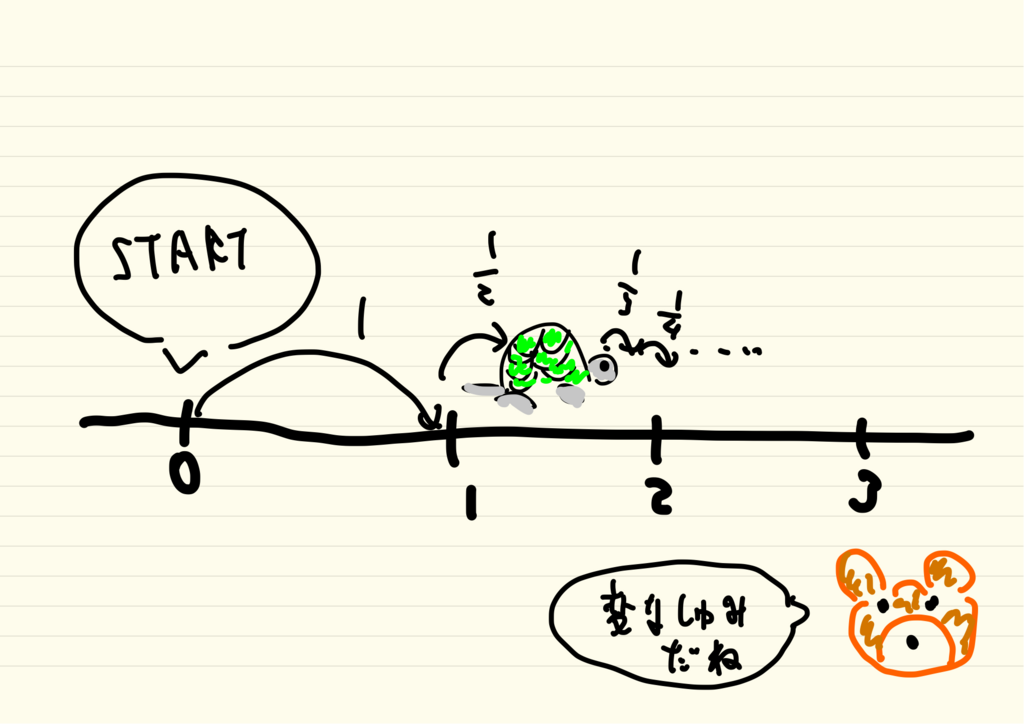
実はオイラー以前にも後にゼータ関数と呼ばれる関数の研究は始まっていました。14世紀のフランスでは、という足し算が無限大になるという事が証明されました。この足し算は調和級数と呼ばれるものです。足す数は
、
、
のようにどんどん
に近づいていくにもかかわらず無限大になるという少し不思議な足し算です。
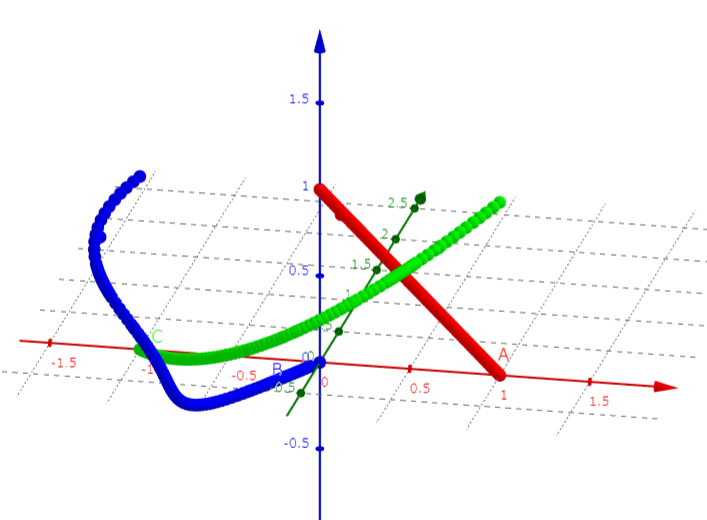
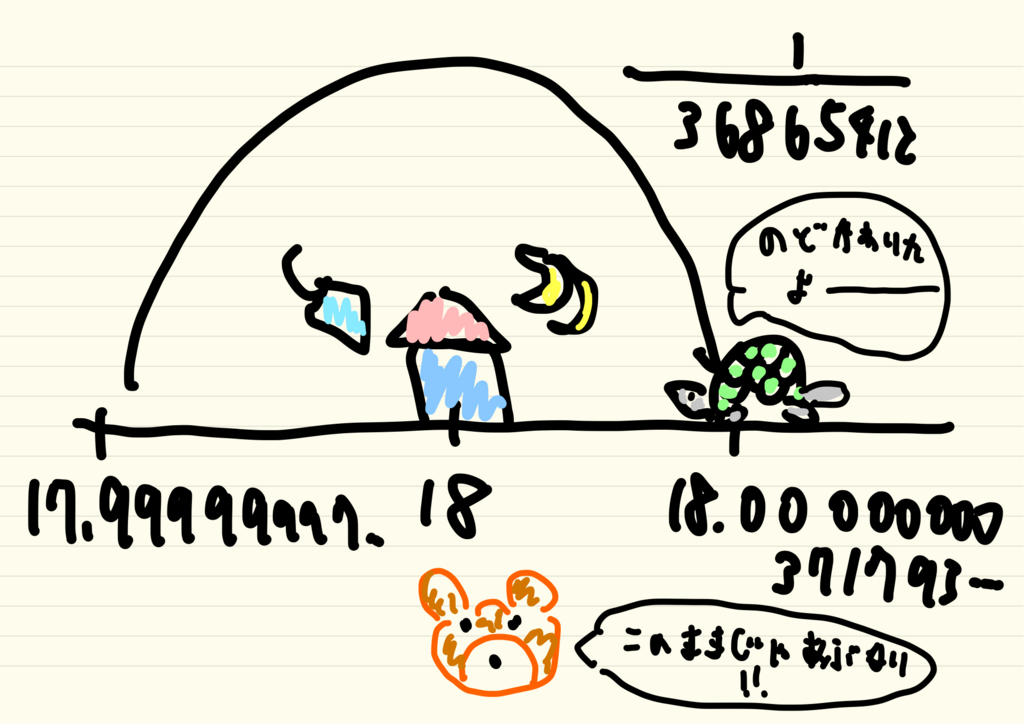
このことをグラフで確認してみましょう。グラフのピンク色の線はこの足し算が増えていく様子を表しています。足す数が小さくなっていくため、ピンク色の線の増え具合はどんどん小さくなっていき、徐々に横軸に対して平行になっていきます。グラフの上部にピンク色の線が超えないと思われる壁(水色の線)を用意しても、足し算を続けていくといつかはピンク色の線が壁を追い越します。さらに大きい壁を用意してもやはりピンク色の線は壁を追い越すのです。
この足し算の分母には「乗」が隠れており、これはゼータ関数に
を入れたものと見ることができます。つまり14世紀フランスでは
であることが証明されていたのです。
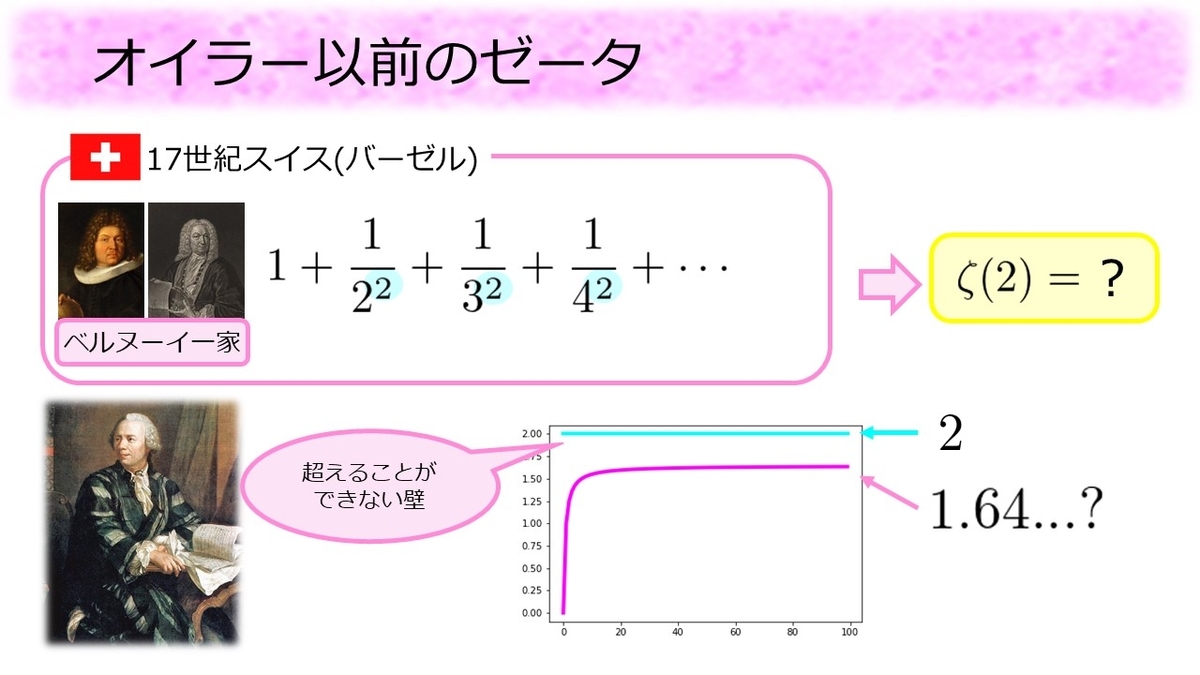
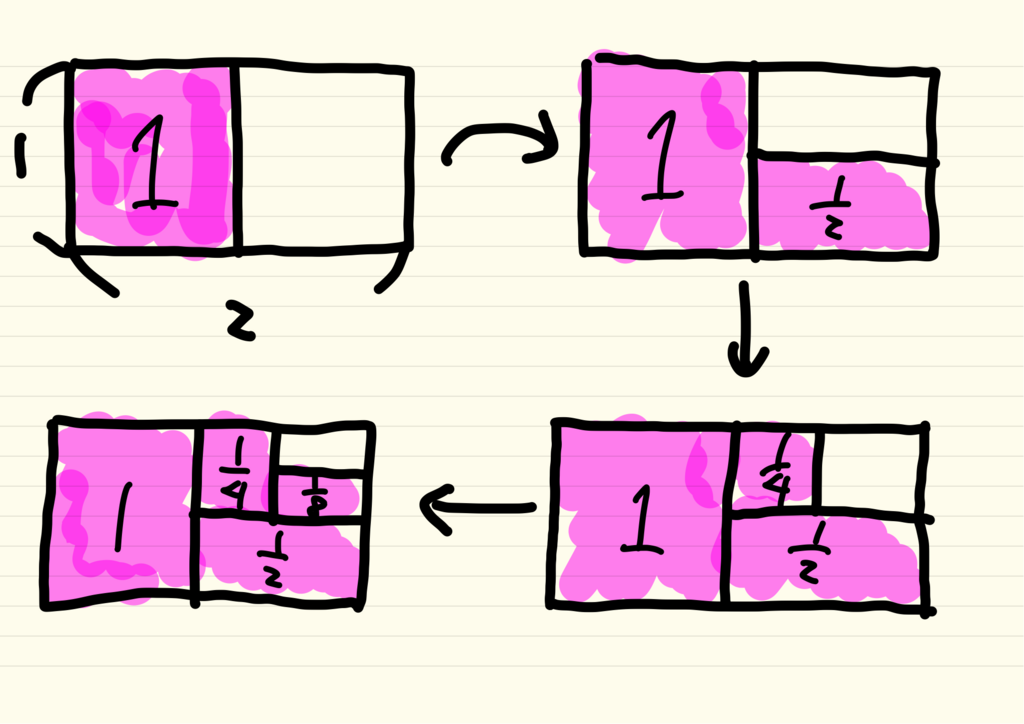
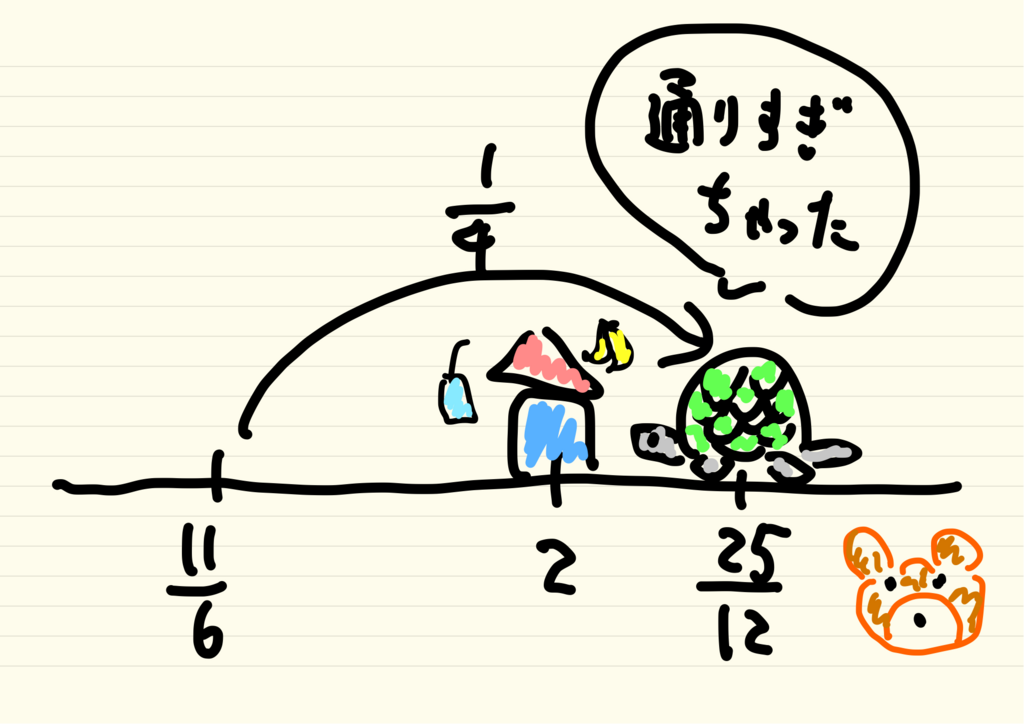
時は流れ17世紀スイスではベルヌーイ一家がの値を求めようと躍起になっていました。この足し算は先ほどの調和級数と違い、絶対に超えられない壁が存在し、その壁の値が
があることは簡単に証明されていました。壁があるという事は何かに近づいていくはずで、手計算の結果
くらいになることはわかるのですが、その値が何なのかわかっていなかったのです。この足し算はゼータ関数に
を入れたものなので、ベルヌーイ一家は
の値を求めようと頑張っていたという事になります。そしてこの問題を解いたのが18世紀にベルヌーイ一家にもよくお邪魔していたオイラーだったのです。この問題はオイラー、ベルヌーイ一家の故郷の地名にちなんでバーゼル問題と呼ばれています。

それではゼータのDNAの1つ目「特殊値」を見ていきましょう。

1735年オイラーは円の弧()、余弦(
)、正弦(
)の間に成り立つ関係式をいじっているうちに、まったく思いがけず
の値にたどり着きます。その値はなんと
になります。これは誠に驚くべきことで、小学生でも理解できて、円とは全く関係のないように見える分数の足し算の先に、が現れるのです。
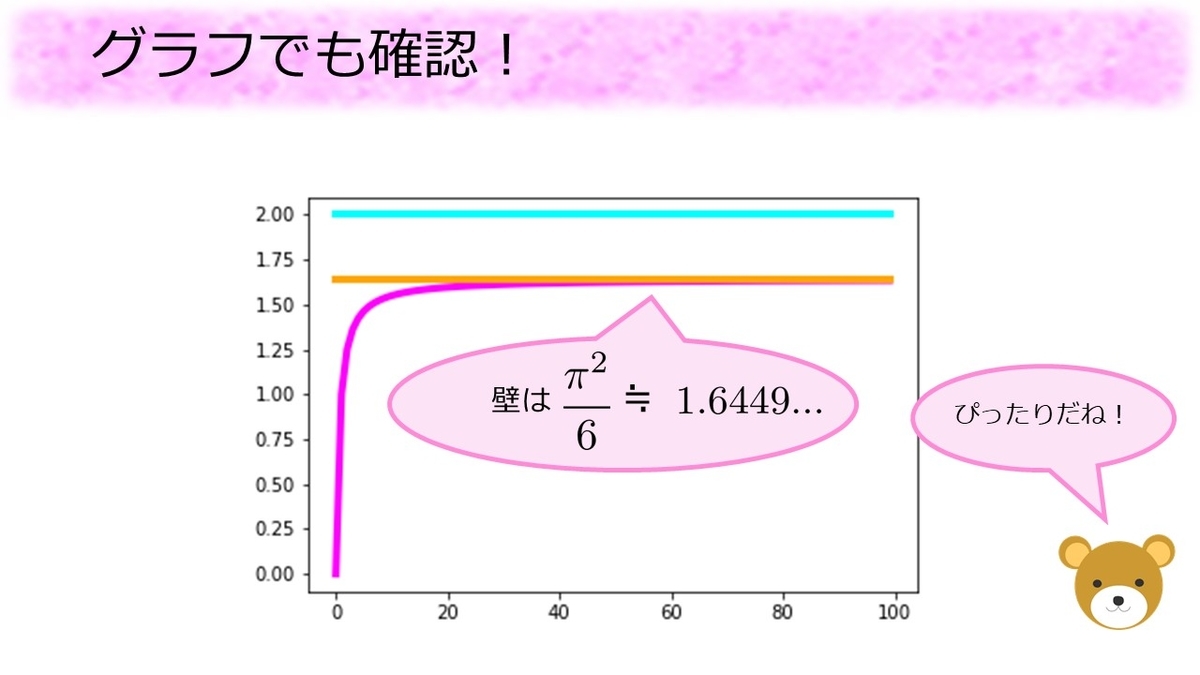
実際にグラフで確認してみます。バーゼル問題の説明に用いたグラフにのオレンジ色の壁を追加すると、ピンク色の線がオレンジ色の壁にぴったり重なっていく様子が確認できます。これは
が
に近づいていっているということに他なりません。
にたどり着いたオイラーの喜びは相当なものだったと想像します。
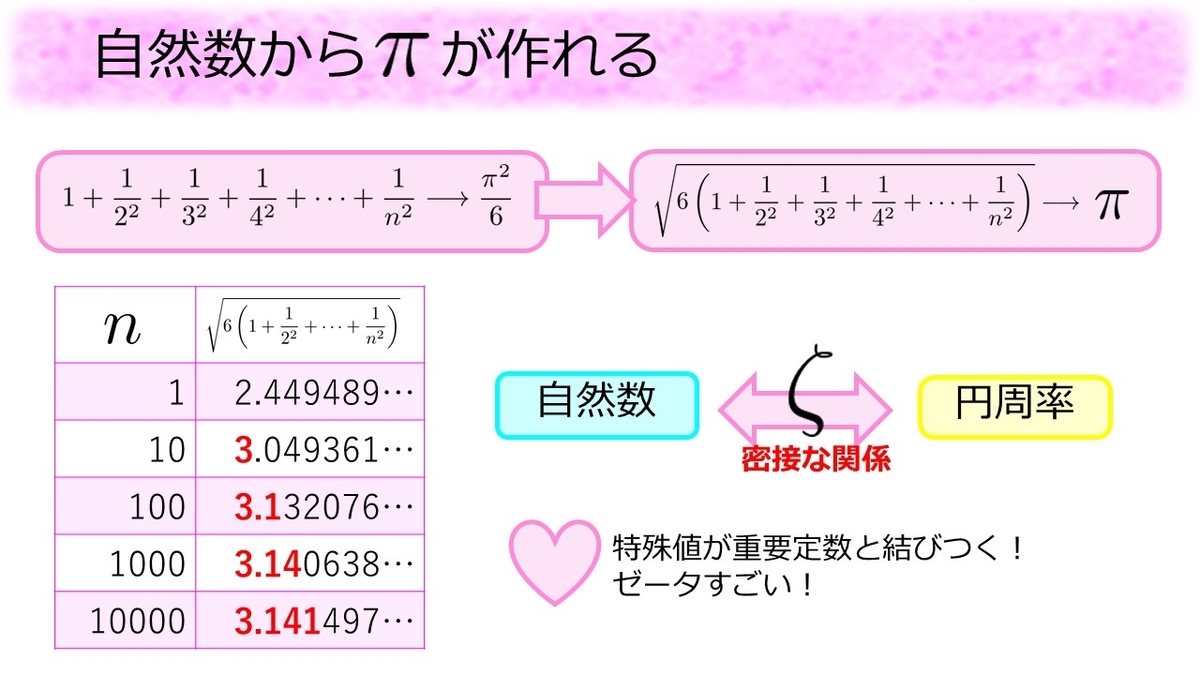
にて、
をどんどん大きくすると、その値が
に近づいていくという事は、それを
倍してルートをとった
が
に近づいていくということを意味します。実際に表を作って確認すると
を大きくするにつれて
に近づいていく様子が確認できます。つまり円も図形も書かずに自然数から円周率が計算できるのです。これは自然数と円周率の間には密接な関係があること、そしてその間をゼータが取り持っているという事を意味しています。
特殊値とはのようにゼータ関数に整数などの代表的な数を入れたときに出てくる、それなりに綺麗な値のことです*1。ゼータ関数の特殊値に
などの重要定数が現れることがあり*2、そのことがゼータ関数の重要性を現わしています。
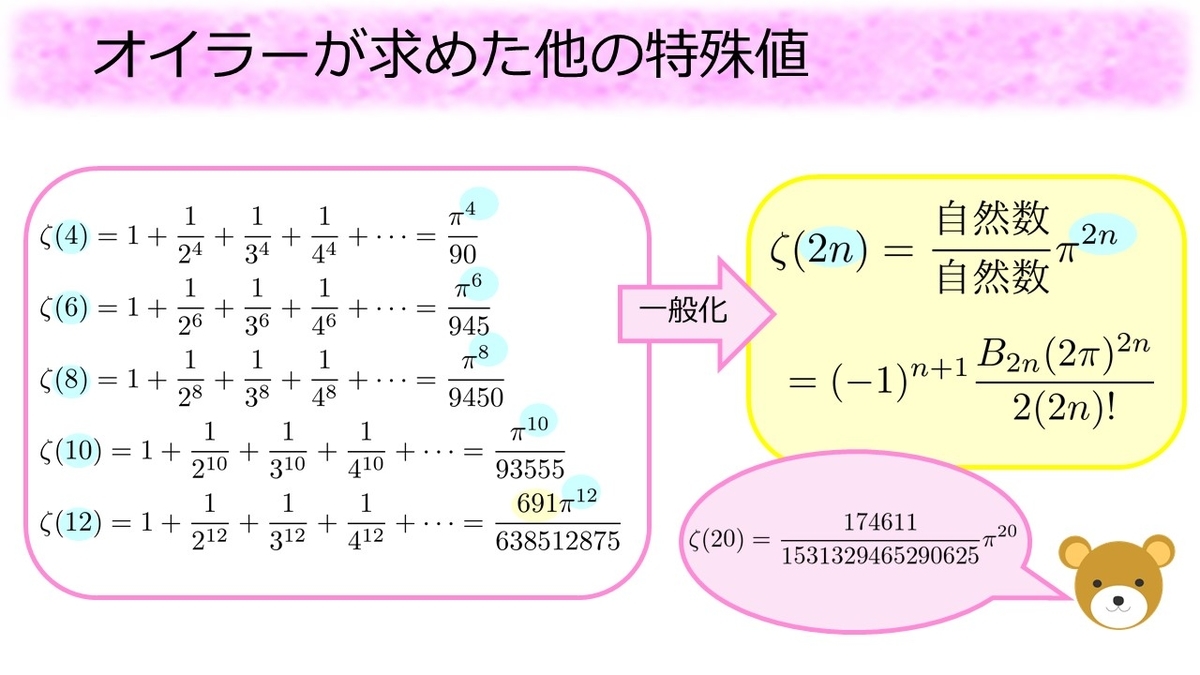
オイラーはだけでなく、他の正の偶数に対しても
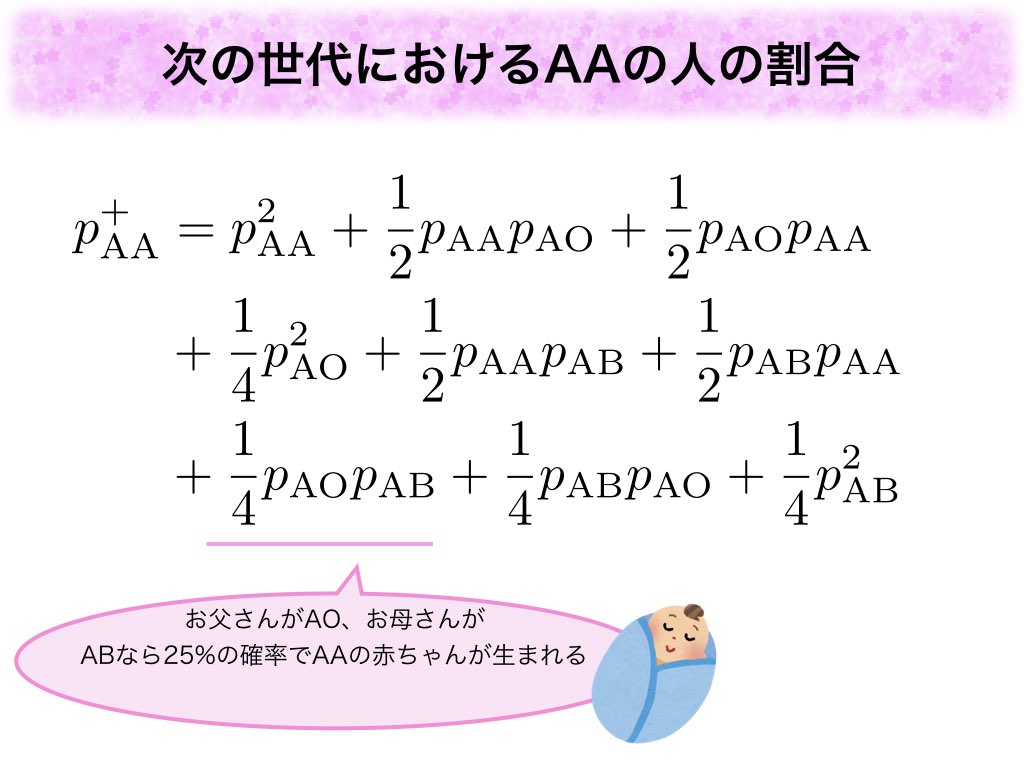
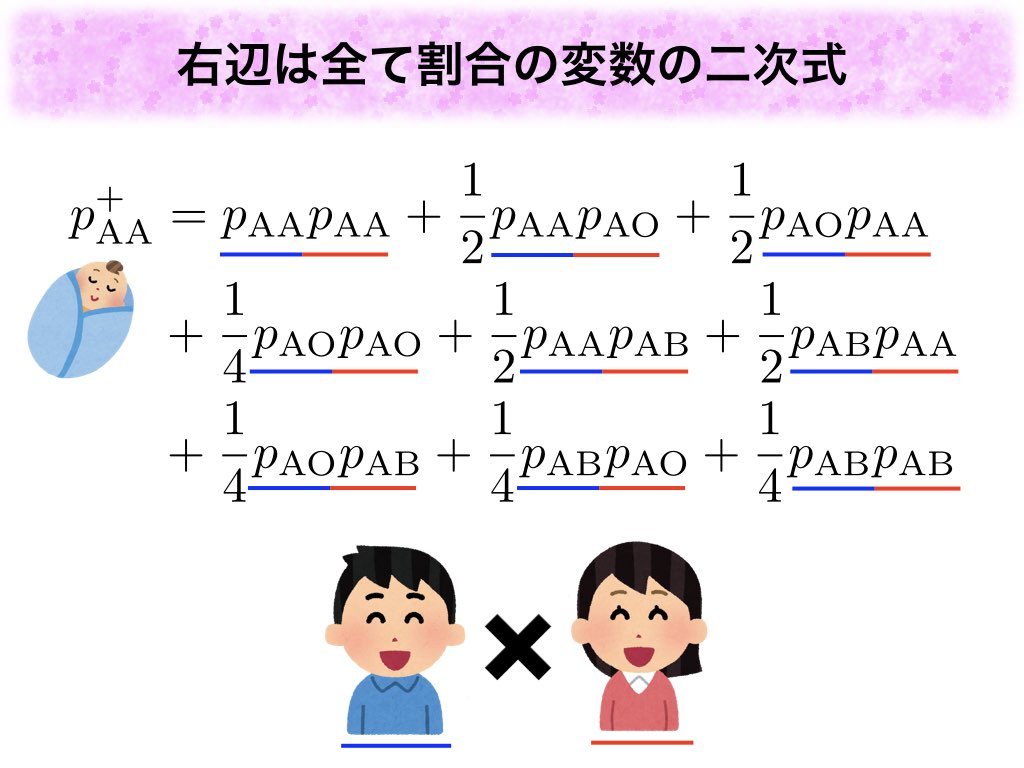
の値を得ていました。それは「自然数」÷「自然数」の形をした分数と
の(ゼータ関数に入れた)偶数乗の積で表せます*3。また分子の自然数部分に注目すると
から
まではずっと
だったにもかかわらず、
で急に
という大きな自然数が出てきており、より深い数学の話とつながっています。こちらに関してはtsujimotterさんのブログを読んでみて下さい。
次にゼータ2つ目のDNAである「オイラー積」の紹介をします。

古来から多くの数学者に愛される数、それは素数です。素数は「と自分自身しか約数を持たない
以上の自然数」ですが、それは
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、、、と不規則に現れます。また、たとえば連続して
個の自然数が素数でないような素数砂漠も存在します*4。
上述のとおり素数は一見、不規則で無秩序のように見えるのですが、数学者たちは長い歴史の中で素数達が織りなす美しい秩序を発見してきました*5。そしてオイラーも1737年に美しい秩序を発見するのです。

ゼータ関数は「自然数の和」の形のように表せるとお話ししたのですが、なんと「素数の積」の形でも表せます。これをゼータ関数のオイラー積表示と呼びます。
例えばとすると
なので、次の式が成り立ちます。
素数から作られる分数の掛け算を続けていくと円周率が現れるというのは本当に驚きです!

先ほど得た式を変形することで、にて素数
を大きくすればするほど、
に近づいていくという事がわかります。表を作って確認すると、確かにその通りになっています。昔東大の入試問題で「円周率が
より大きいことを証明せよ」というものがありましたが、この関係式を使うとたった
個の素数に対して簡単な計算をすることで証明できることが分かります。
ゼータ関数のオイラー積表示によって素数と円周率の間にも密接な関係があることがわかりました。ゼータ関数の背後には数学者たちを魅了して止まない素数が潜んでいる。これこそゼータ関数の最大の素敵ポイントです!

次のDNAは関数等式です。

関数等式を数式で書くとこのように難しいように思えるのですが、そこは理解する必要はありません。大事なポイントはの値が分かれば
の値がわかるという事です。
オイラーのおかげで私たちはゼータ関数に正の偶数を入れたときに出てくる特殊値を知っています。関数等式を使うことでまだ見ぬゼータ関数の特殊値を知ることができ、なんとそこには不思議な足し算が現れるのです。
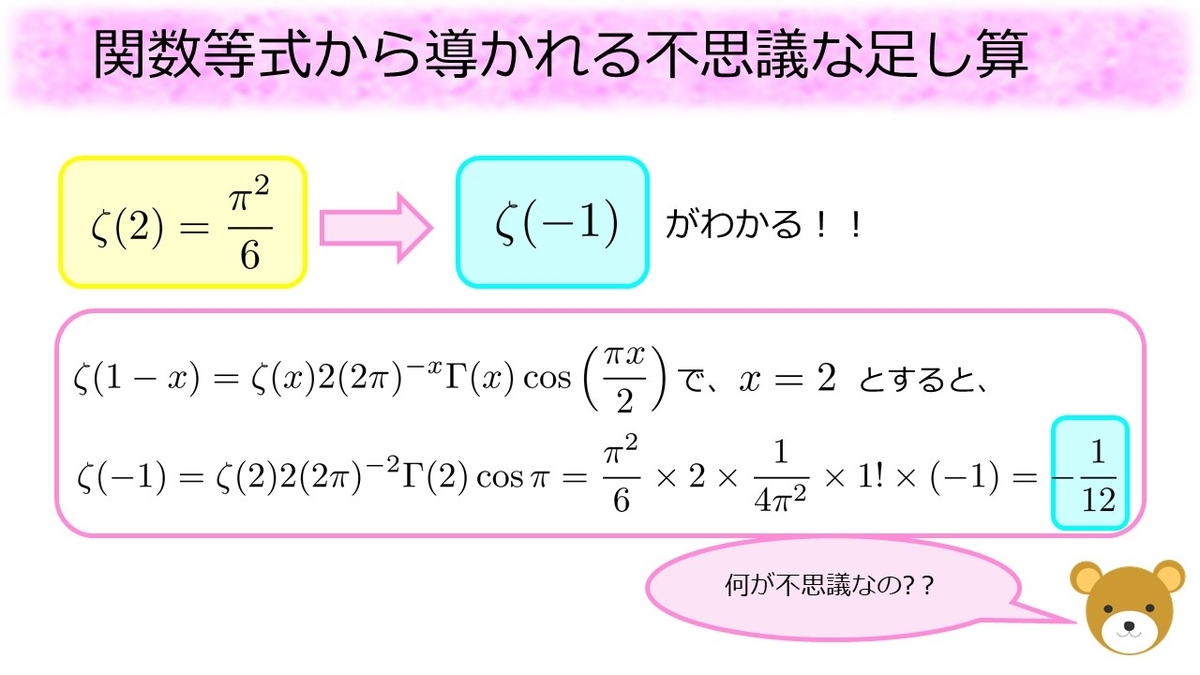
実際に関数等式においてとしてみると、簡単な計算で
であることが分かります。どこが不思議なのでしょうか?

ゼータ関数の定義に戻ってみるとと表せますが、
乗というのは逆数をとることなので、この足し算は
となります。つまり
という式は、
を意味しているという事になります。
より大きいものを足していって、負の数が現れる、しかも自然数を足しているのに分数の形で現れる。何とも不思議ではないでしょうか?

オイラーは他にも不思議な足し算をたくさん見つけています。「オイラー頭おかしくなったんじゃない?」って思ってしまいますが、オイラーは論文の中で「和についてさらに拡張した定義を与えなければならない ~(中略)~ それは解析的な手法で展開することによって同様な級数を導き~」と述べており、これは後の時代に「解析接続」と呼ばれる理論をオイラーが強く意識していたことに他なりません。オイラーの先見の明に驚かされます。
関数等式によってゼータ関数から不思議な足し算が現れました。これもゼータの魅力の一つです。また、関数等式はと
の対称性を表しているのですが、これはリーマン予想と強く関係しています。
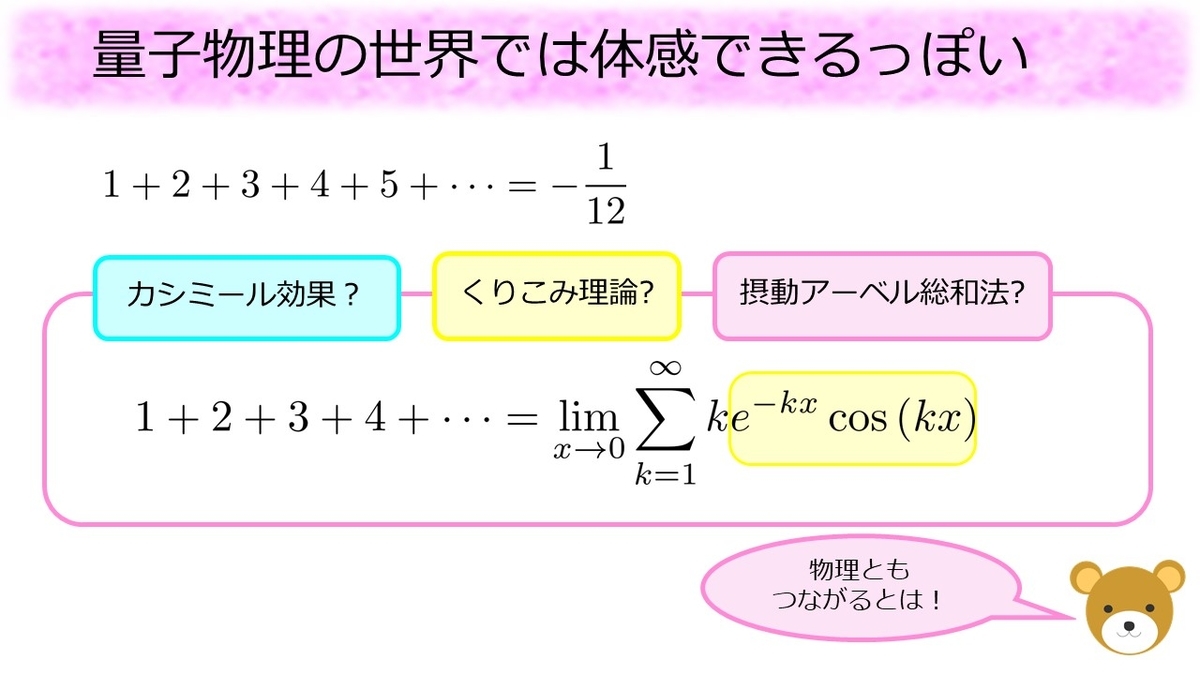
という式は、本当に不思議な足し算ですが、どうやら量子物理の世界では現象として観測できるそうです。この辺りは全く詳しくないので完全に紹介程度になるのですが、
の足し算は
や
という記号を使う事で、別の形で書き表すことができます。数学に詳しい方は
を
に近づけることで黄色で塗った部分が
に近づくこと、したがって左辺と右辺が一致することが分かるでしょう*6。この右辺において
と固定し、
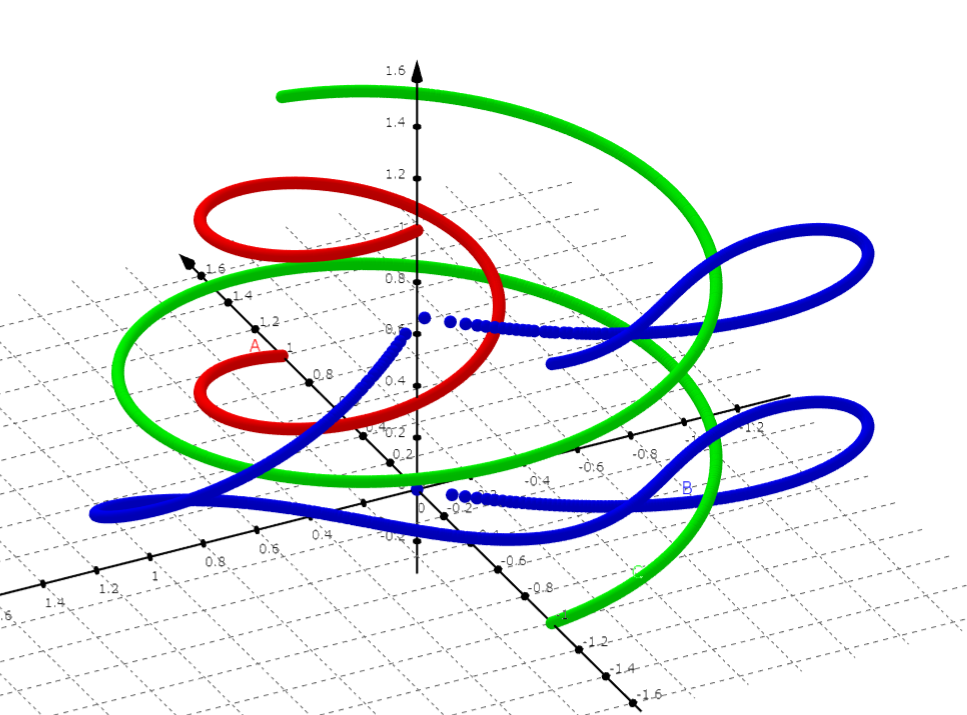
の足し算をしていくにつれて値がどう変わるのかをグラフで可視化してみます。
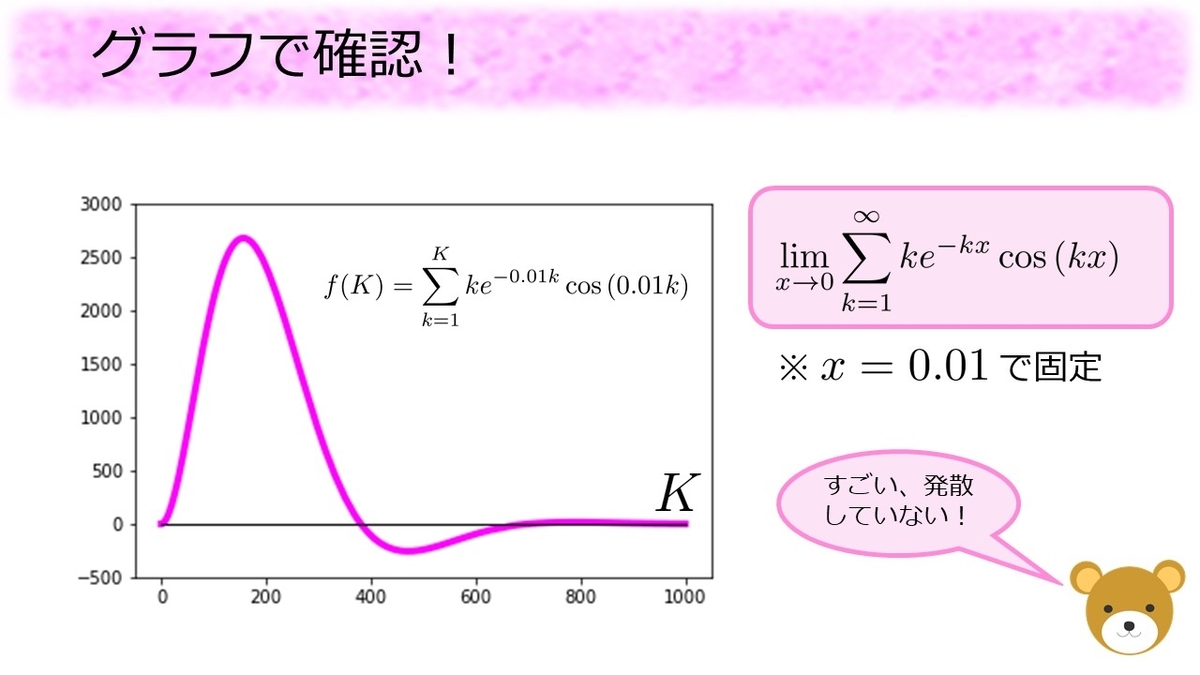
すると、最初の方ではと同じスピードで増えていくのですが、次第に増え方が減っていき、
個くらい足した辺りから減り始めます。また
個くらい足した辺りから増え始めており、上下に揺れながら
に近い値に近づいていることがわかります。
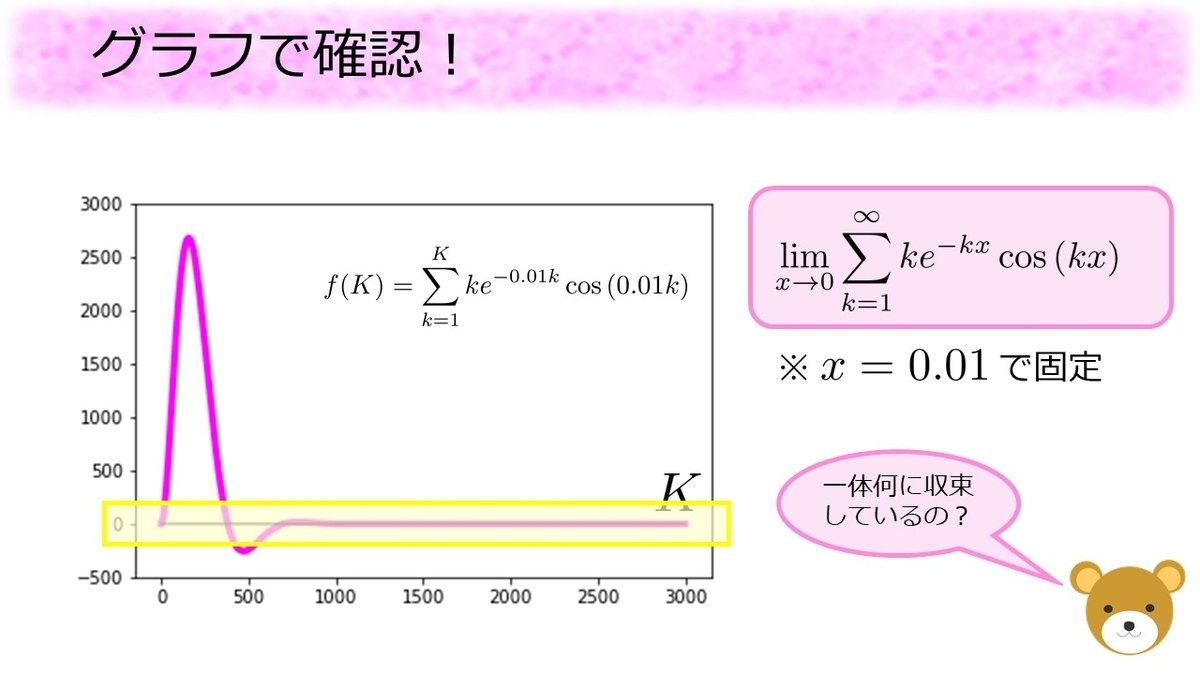
個くらいまで足してみても、確かに何らかの値に近づいているようです。そこでグラフの黄色い部分を切り出し、上下に拡大してみます。
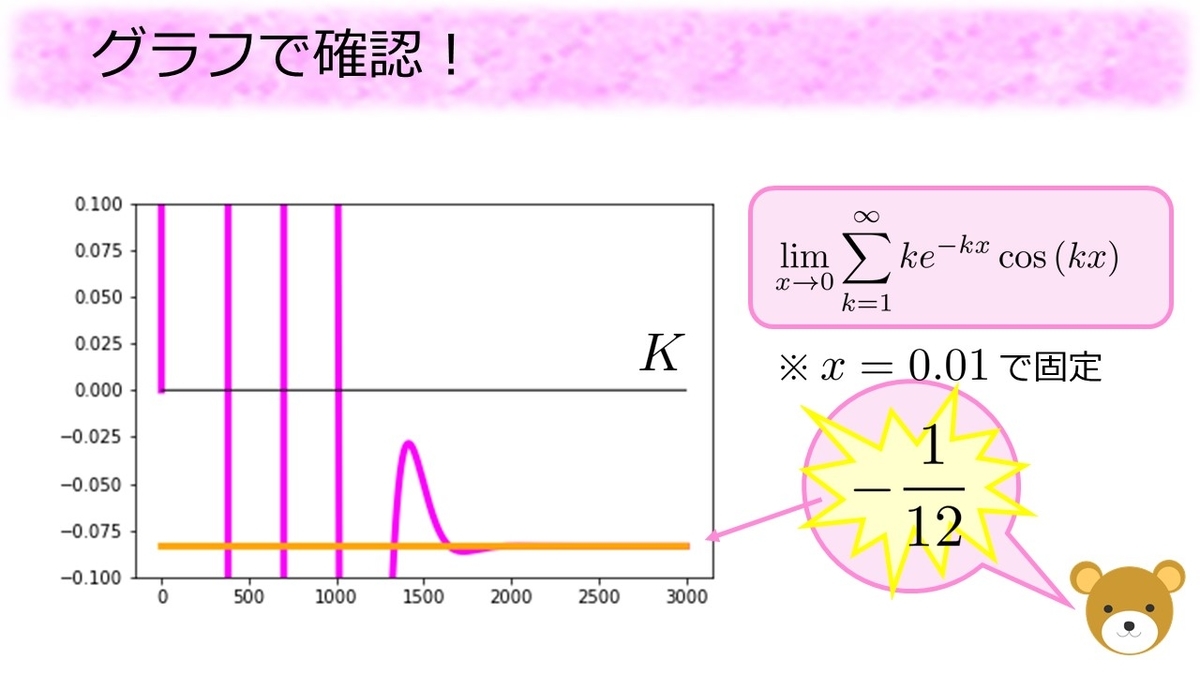
グラフにオレンジ色の直線でのグラフを書き加えると、グラフの右側ではピンク色の線とぴったり一致します。ちょっと強引な式で
を別の形で表したのですが、その式のグラフが
に近づく。。。近づけと一言も言っていないのに近づいている、近づいてしまう!これは
が正しそうと裏付ける証拠になっているのではないでしょうか。
この等式に関しては、こちらのサイトを参照させていただきました。だけでなく、
~
まで計算したのですが、たしかにオイラーによって求められた特殊値に近づいていくことが確認できました!
xseek-qm.net

じつは関数等式からもう一つ面白いことが分かります。を
以上の奇数とすると、
より、ゼータ関数の負の偶数での値が
であることがわかります。これは自明な零点と呼ばれるもので、リーマン予想にもつながるとても重要なものになります。
ゼータ関数の零点に関しては昔手計算したことがありますので、良かったらこちらも参考にしてください。
mattyuu.hatenadiary.com

最後のDNAは積分表示です。

積分表示はゼータ関数を解析学の代表的な言葉である積分の形で表すことができるというものです。リーマンは「リーマン積分」や「コーシー・リーマンの方程式」など解析学に多くの業績を残した解析学の分野の権威であったため、ゼータ関数がリーマンが扱いやすい形に表示できているという事になります。実際1859年のリーマン予想が生まれた論文は、この積分を変数変換した数式が出発点になっています。
以上で、ゼータ関数の4つのDNAの紹介を終わります。

さてプレゼンタイトルの「オイラーからの贈り物」というのはオイラーが発見し、リーマンが受け取ったゼータ4つのDNAを意味していました。実はリーマンに贈り物を送ったのはオイラーだけではありません。それはリーマンの少しだけ前の時代に活躍し、同じドイツ、同じゲッティンゲン大学でリーマンと交流もあった大数学者ガウスです。ガウスがリーマンに送ったものそれは素数階段です!リーマンはオイラー、ガウスという大数学者から贈り物をもらい、独自に研究し1859年の論文が完成します。その論文の中で「リーマン予想」が誕生するのですが、160年経過した今でも証明されていません。リーマン予想はリーマンから私たちへの贈り物です。
リーマンは1859年の論文にてゼータ関数の零点を知ることで素数の分布がわかる(=素数階段が再現できる)ということを証明しています。そちらに関してはやはりtsujimotterさんのブログを読んでください。
tsujimotter.hatenablog.com
今回はゼータ関数をから説明したわけですが、実は大きな嘘がありました。本記事でゼータ関数として紹介してきたものは、「リーマン・ゼータ関数」と呼ばれるものです。実は他にもゼータ関数はたくさんあり、ロマ数ゼータでも多数紹介されました。では、ゼータをゼータたらしめるものは何でしょうか。

実はどういう関数をゼータ関数と名付けてよいのかははっきりとした決まりがなさそうです。ゼータ関数を研究されている数学者の方々が「ゼータは人の心を魅了するもの」、「ゼータ惑星の生き物」と述べているように、数学者にとってもゼータは捉えようがなく、不思議で心ときめくものなのでしょう。しかし1つ言えることはどんなゼータ関数も今回述べたような4つのDNAをだいたい持っていることです。
例えば、
「オイラー積」のような形で定義された新しいゼータ関数が、「積分表示」によって研究しやすい対象になり、「特殊値」が重要な数学定数と結びつくことで心ときめき、「関数等式」の対称性によってクリティカルラインが得られ、そのゼータ関数のリーマン予想が定式化される。
ロマ数ゼータの他の方々のプレゼンにも今回紹介した4つのDNAが何度も登場しましたし、後で気づいたのですがロマ数ゼータのロゴにも全てのDNAが登場していました!
以上で、プレゼン内容の紹介を終わります。今回紹介した内容は本当にゼータの不思議な世界の入り口にすぎません。まだまだ楽しい話はいくらでもあるので本文中に参考に挙げた記事や、ロマ数ゼータの他の方のプレゼンをYouTubeで見てみて下さい(4:43:40あたりからロマ数ゼータが始まります)。
Part 3: 数学の楽しみ方の見本市「マスパーティ」(10/20 10:45 ~ 19:30)
また、難しく感じた方はになることだけでも心にとどめてくれたら嬉しいです!実はマスパーティの参加者、スタッフ、登壇者に配られた缶バッジの背景には
、
、
の値が刻まれていました。宝物にします!

最後に、本記事は黒川信重先生の下記書籍を参考にさせていただきましたので、紹介させていただきます。

- 作者: 黒川信重,小山信也,馬場郁,高田加代子
- 出版社/メーカー: 日本評論社
- 発売日: 2018/08/28
- メディア: 単行本
- この商品を含むブログを見る