リーマンゼータ関数のゼロ点を手計算してみた

10/1に第7回日曜数学会で掲題の件でLTをさせていただきました。
拙い発表でしたが、自分の好きな数学に関して発表する機会を作っていただき、日曜数学会の幹事のキグロさん、tsujimotterさん、塩鯖さんに厚く御礼を申し上げます。

また、休憩時間や懇親会にてその他多くの参加者の皆様とも話させていただき、とても有意義な時間が過ごせました。
数学の話題しか出ない懇親会はとてもいいものですね。
皆様ありがとうございました。

私の発表に対してtwitterでつぶやいてくださった方がいらっしゃり大変嬉しかったです。
ありがとうございます。
私はつぶやいたことがなかったのですが、つぶやいてもらえると嬉しいということがわかりましたので、今後日曜数学会に参加した際は全力でつぶやかさせていただきますのでよろしくお願いします。

さて、昨日の発表ですがせっかくなので公開したくブログを作成しました。
日曜数学会のLTは5分という短い時間で伝えたいことを伝えなければいけません。
5分に全力をかける、5分で伝えたいことを凝縮するという点でとても勉強になりましたが、本当は説明したかったところを泣く泣く削ることがありました。
この記事ではそういったところも含めて発表資料のスライドを紙芝居のように使いながら説明させていただこうと思います。
今後リーマンゼータ関数のゼロ点を手計算したい方がいらっしゃいましたら、ぜひ読んでいただけたらと思います。

(本来こういった発表は前提とする数学的知識を明確にすべきなのですが、今回はあまり考えておりませんでした。。。世間一般では複素数とはどれだけ浸透しているのでしょうか。。複素数とは何かといった説明は全くありません。。)
(実際に紙芝居のようにまとめてみると文字数が1万字を超えてしまい、相当のモチベーションがある人じゃないと最後まで読んでもらえないだろうと思います。ただこういう風にまとめておくのは今後の自分のためにもなると思い、公開します。)

始まり、始まり
f:id:mattyuu:20161002134126j:plain
↑
「リーマンゼータ関数のゼロ点を手計算してみた」というタイトルで発表させていただきます。

f:id:mattyuu:20161002134143j:plain
↑
リーマンゼータ関数とは何かというと、18世紀にオイラーが研究し、1859年にリーマンの記念碑的論文「与えられた数より小さい素数の個数について」で ${\zeta(s)}$ という記号で名付けられた関数で、自然数の $s$ 乗の逆数の無限和で定義されます。 $s$ が変数で、 $\zeta$ (←ゼータと読みます)が関数名となります。注意したいことはこの関数は通常中学校で学ぶ関数とは異なり、複素変数で複素数値を返す関数になるところです。つまり、変数 $s$ と $\zeta(s)$ は複素数になります。

例えば $s=2$ とすると、 $\zeta(2)$ は平方数の逆数の無限和になりますが、なんとこの無限和は $\frac{\pi^2}{6}$ と等しくなります! これは誠に驚くべきことで、小学生でも理解できて、円とは全く関係のないように見える分数の足し算の先に、 $\pi$ が現れるのです。この級数が無限大にならず収束することは容易に分かるのですが、誰もその値に辿り着けずにいました。1735年に人類で初めてオイラーがこの級数が $\frac{\pi^2}{6}$ と等しくなることを発見、証明しました。とても美しいですね。私は学生時代に学んだ数式の中で2番目にこの数式が好きです(1番はコーシーの積分公式です。)。

関数の記号は $\zeta$ なのに、この関数の名前には"リーマン"もしくは"リーマンの"という風に接頭語がつきます(接頭語という表記が正しいかはわかりませんが。)。これは後の時代に様々な $\zeta$ 関数が見つかっているからのようです。私はまだ勉強中の身であるためこれ以上は語ることができません。

f:id:mattyuu:20161002134148j:plain
↑
今回なぜリーマンゼータ関数のゼロ点をテーマに選んだかをお伝えします。
それは、リーマンゼータ関数のゼロ点は、人類が抱える問題の中で間違いなく最難関の部類に入る未解決問題リーマン予想と密接に関係しているためです。リーマンゼータ関数のゼロ点とは $\zeta(s)=0$ となるような $s$ のことであり、マイナスの偶数がゼロ点になることは容易に証明できます。これは自明なゼロ点と呼ばれます(スライドの水色の点となります。)。

$\zeta(-2)=0$ ?と不思議になられた方もいらっしゃるかもしれません。それは $\zeta(s)$ を自然数の逆数和で表記した時に、明らかにゼロにならないように見えるからです。
${ \displaystyle \zeta(-2) = \sum_{n=1}^{\infty} \frac{1}{n^{-2}}=1+2^2+3^2+4^2+\cdots = 0 (?) }$
実は $\zeta(s)$ を自然数の逆数和で表記できるのは $\rm{Re}(s)>1$ の時だけであり、 $\rm{Re}(s)\leq1$ に対しては解析接続という技術を使って関数を表記しなおさなければいけません。ここでは「解析接続が必要なんだよ」というところで説明は省かせていただきます。

さて話を戻すと、マイナスの偶数という自明なゼロ点以外にもリーマンゼータ関数のゼロ点が存在します。それらは非自明なゼロ点と呼ばれます(スライドのピンク色の点となります。)。リーマン予想とは「リーマンゼータ関数の非自明なゼロ点は一直線上に並んでいるはずだ」という予想になり、この一直線とは実部が $\frac{1}{2}$ の直線になります(スライドのピンク色の点線になります)。

リーマン予想が生まれて160年弱、世界中の大天才達が挑み、未だ証明できていません。このことを考えるだけでもゼロ点が凄いものということがわかっていただけると思います。

「天才達が挑んだ歴史なんてどうでもいい、そもそもなぜゼロ点が重要か? ゼロ点がどこかわかって何かいいことある?」と思われる方もいらっしゃるかもしれません。すみません、私の力不足で詳しく色々語ることができないのですが、世の中にはリーマン予想が正しければ正しいという定理が何千もあるようです。それだけリーマン予想は数学の根底に関わる問題なのでしょう。リーマン予想を証明することは多くの数学者が最後のピースを埋められずに証明できていない、数々の定理を証明することになるのです。

f:id:mattyuu:20161002134153j:plain
↑
次に、なぜゼロ点を手計算したくなかったを説明します。
2009年のNHKスペシャル「魔性の難問　リーマン予想・天才たちの闘い」を見たところ、「実際のゼロ点の位置を、まず4つほど求めたリーマンは予想外の事実に気づきます。」というナレーションと共に、リーマンが驚いている描写がされておりました。また当時のリーマンの計算用紙も紹介されておりました。リーマンゼータ関数は無限和や無限区間の積分で定義されます。1859年というコンピュータのない時代にどうやってゼロ点を手計算したんだろう? と疑問に思ったことがきっかけです(今回、実際にはリーマンの計算方法ではなくグラームの計算方法で計算しております。)。

f:id:mattyuu:20161002134159j:plain
↑
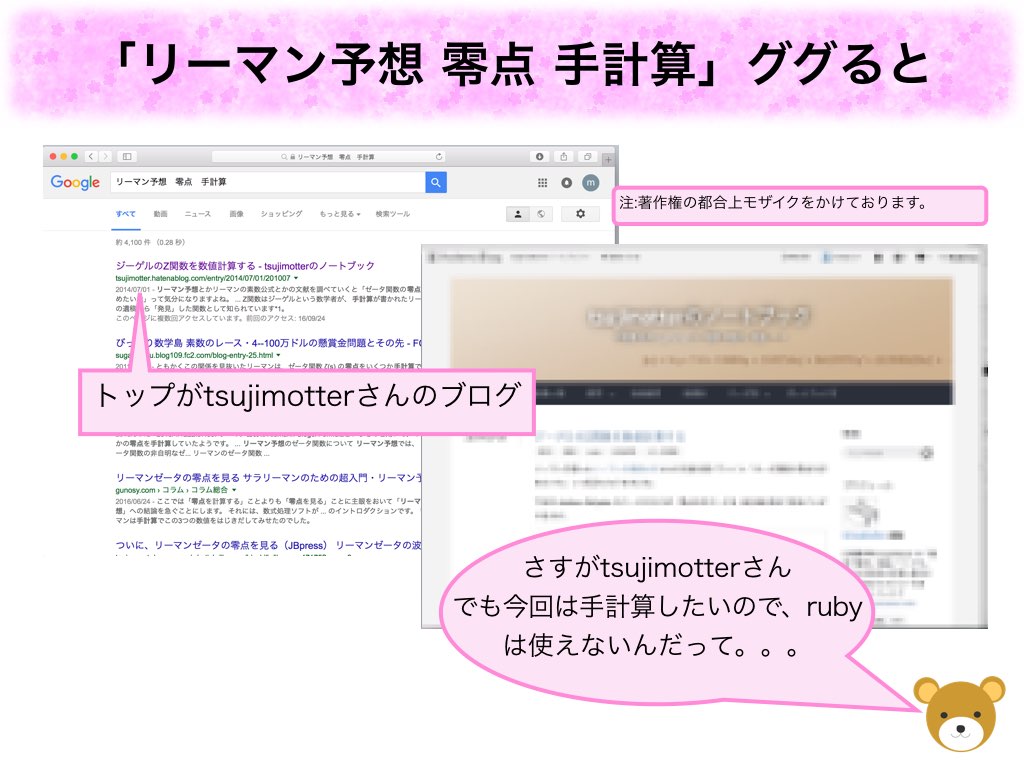
リーマンゼータ関数のゼロ点を手計算する方法は私が探した限りネット上では見つけることができませんでした。

なお、「リーマン予想零点手計算」でgoogle検索を行うと、tsujimotterさんのブログが一番に出てきました。

ジーゲルのZ関数を数値計算する
ジーゲルのZ関数を数値計算する - tsujimotterのノートブック

私がご紹介するのもおこがましいのですが、tsujimotterさんは日曜数学者の生みの親であり、私の憧れであります。数学会では3Dプリンタでリーマンゼータ関数を可視化したことで有名です。ゼロ点がなぜ重要か? ということに関しても、下記の記事にて、リーマンの素数公式の右辺に出てくるためであるという新たな知見を私に与えてくれました。(ここまで不思議と素数について記載していなかったのですが、リーマンゼータ関数のゼロ点は数学者たちが愛してやまない素数の情報をすべて持っているとも言えるのです。)

リーマンの素数公式を可視化する
リーマンの素数公式を可視化する - tsujimotterのノートブック

ただtsujimotterさんのブログではゼロ点をruby(←プログラミング言語)を用いて計算しております。私はコンピュータのない時代にどうやって計算したかを知りたいため、tsujimotterさんのブログだけでは疑問を解消することができませんでした。

f:id:mattyuu:20161002134205j:plain
↑
リーマン予想とゼロ点計算の歴史を簡単に紹介します。リーマン予想が1859年に世に生み出されたことは既にお伝えした通りですが、リーマン予想は1900年のヒルベルトの23の問題、2000年のミレニアム懸賞金問題に選出されております。
ヒルベルトの23の問題とは、1900年にドイツのヒルベルトという有名数学者が20世紀に解くべき数学の23個の未解決問題をまとめたものです。同様にミレニアム懸賞金問題とは、2000年にクレイ研究所が定めた数学上の7つの重要未解決問題のことであり、解決した数学者には100万ドルの懸賞金が与えられるとのことです。1900年、2000年と100年経っても数学会の最重要未解決問題であり続けるリーマン予想のラスボス感を思い知らされます。

驚くことに1900年のヒルベルトの23の問題が発表された当時、人類は非自明なゼロ点に関する数値情報を1つも持っていなかったようです(リーマンただ一人を除いて)。初めて(リーマンを除く)人類が非自明なゼロ点を目にしたのは、1903年グラームの研究結果となります。今回は鹿野健先生編著の「リーマン予想」(日本評論社)を参照して、グラームの方法でゼロ点を手計算しました。

なお、リーマンは研究結果を論文として公表しますが、その結果に至った証明、計算過程のメモを公表することはなかったようです(←リーマン予想に関してだけかもしれません)。そのため1900年代にリーマン予想を証明しようとしてできなかった数学者達に、「リーマン予想は成り立たないのであろう、リーマンは計算していないのだから、リーマン予想は夢想だろう」という風に思われたことがあるようです。1932年ジーゲルというドイツの数学者がその驚くべき洞察力で、リーマンが残した断片的なメモを解読し、リーマンがゼロ点を実際に手計算していたという事実、またゼロ点を計算するのにグラームの方法より有用な公式(←今日ではリーマン・ジーゲルの公式と呼ばれています)を導いていたことを発見します(NHKスペシャルのナレーションには嘘がなかったことになります。)。リーマンは頭脳だけで定理を見つけるような天才ではなく、実際には膨大な手計算を元に定理を導くエレファントな一面もあったわけです。

今回、リーマンが実際に用いたリーマン・ジーゲルの公式は用いず、グラームの方法でゼロ点を計算しています。これはリーマン・ジーゲルの公式がリーマンの天才的頭脳を持ってして思いつく積分路の変更と、エレファントで複雑な計算を経て得られる異形な式であり、ぱっと見なぜこれを計算することでリーマンゼータ関数のゼロ点が計算できるかわからないためです。それに比べグラームの方法は初等的と言え、リーマンゼータ関数を計算しているという実感を得ることができる方法になっており、日曜数学会の発表ではグラームの方法の方が適切と考え、そのようにいたしました。

f:id:mattyuu:20161002134213j:plain
↑
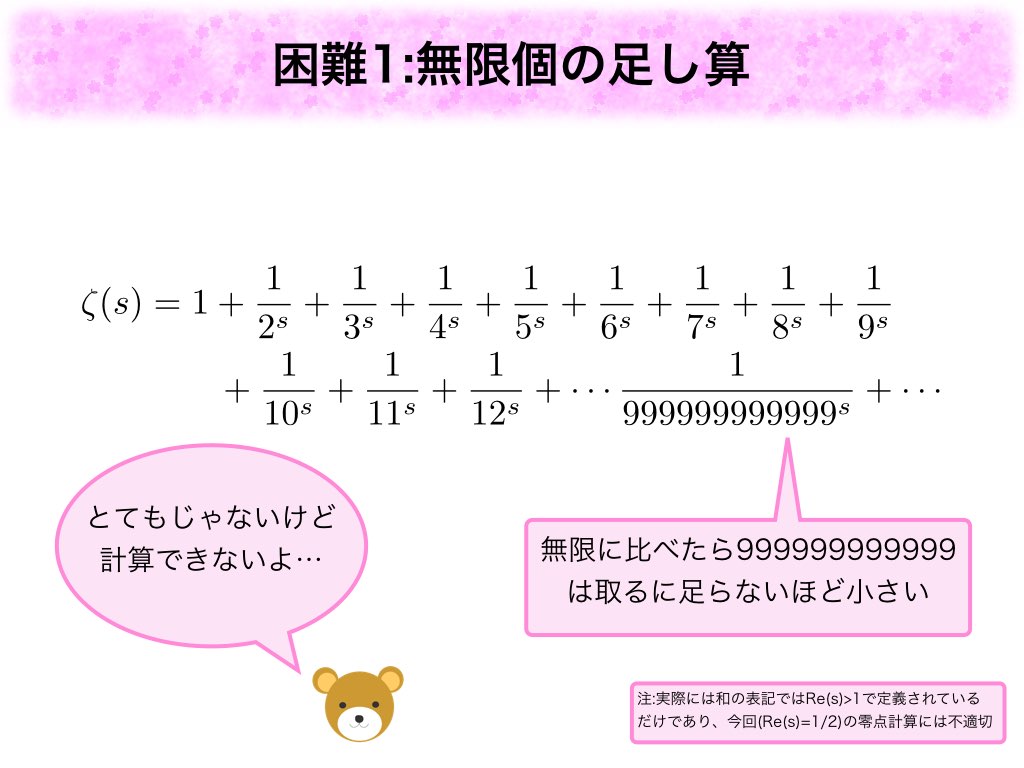
リーマンゼータ関数のゼロ点を計算する中で困難が2つあります。まず1つ目はリーマンゼータ関数は無限個の足し算で定義されていることです。上記のように足し算を $\frac{1}{999999999999^s}$ まで計算したとしても、まだまだ足し算を止めるわけにはいきません。

f:id:mattyuu:20161002134226j:plain
↑
そこでグラームが採用したのがオイラー・マクローリンの和公式です。この公式自体はオイラーが導いたものでリーマンゼータ関数とは直接関係ありません。ここではこういう便利な公式があるというくらいの認識で問題ありません。

f:id:mattyuu:20161002134233j:plain
↑
オイラー・マクローリンの和公式にて、 $N=\infty$ 、 $f(z)=1/{z^s}$ として、
$\displaystyle \zeta(s)=\sum_{n=1}^{M-1}\frac{1}{n^s}+\sum_{n=M}^{\infty}\frac{1}{n^s}$
とすることで、上記の式を導くことができます。

まず主要項と呼ばれる部分ではリーマンゼータ関数を最初の $M-1$ まで真面目に計算します。その次の補正項と呼ばれる部分で計算していない残りの部分の $k$ 次の近似が与えられます( $k$ を大きくすることで誤差が小さくなります)。近似の精度は $M$ 、 $k$ を大きくすることで上げることができます。スライドでは説明していませんが、誤差項 $R_{2k}$ は下記のように上から評価できます( $\sigma={\rm Re}(s)$ です)。

$\displaystyle \left|R_{2k}\right| \leq \left|\frac{s+2k+1}{\sigma+2k+1}\right|\left|\frac{s(s+1)(s+2)\cdots(s+2k)}{(2k+2)!}\right| \left|B_{2k+2}\right|M^{-\sigma-2k-1}$

なお、計算したい非自明なゼロ点( $s=1/2+it)$ の $t$ が大きくなるにつれて、十分な精度でゼロ点を計算するためには $M$ 、 $k$ をどんどん大きくしていく必要があります。例えば $t=10$ であれば、 $M=10$ 、 $k=10$ とすることで、誤差項の絶対値を $10^{-15}$ よりも小さくできますが、 $t=50$ となると、 $M=10$ 、 $k=10$ としても、誤差項の絶対値が $10^{-2}$ 程度まで大きくなってしまいます。実際に手計算をやってみればわかりますが、 $M$ 、 $k$ が1大きくなるだけで、計算をする気力がどっと落ちてしまいます。これはグラームの方法の欠点となっています。

とはいえ、オイラー・マクローリンの和公式を使うことで無限個の和という掴みどころのなかったリーマンゼータ関数を、誤差の大きさを評価できる有限回の計算に落とし込むことができました。これは大きな進歩と言えます。

f:id:mattyuu:20161002134240j:plain
↑
ここまで数式のみの続きイメージがしにくかったですが、実際に $s=1/2+5i$ (つまり $t=5$ )、 $M=5$ 、 $k=3$ とした場合の展開式を紹介します。式は長いですが、これを実直に計算することで $\zeta(1/2+5i)$ を手計算できるのです。

f:id:mattyuu:20161002134248j:plain
↑
ところで、
$\displaystyle \frac{1}{2^{\frac{1}{2}+5i}}$
はどうやって計算するのでしょうか。
実はまたまたオイラーが見つけた公式である、
$\displaystyle e^{i\theta}=\cos{\theta}+i\sin{\theta}$
を用いて、上記のように計算できるのです。
なお、オイラーの公式にて $\theta=\pi$ として右辺を左辺に移行した、
$\displaystyle e^{i\pi}+1=0$
は、ネイピア数 $e$ 、円周率 $\pi$ 、虚数単位 $i$ 、和の単位元 $0$ 、積の単位元 $1$ が1つの式で結ばれており、その美しさから人類の至宝と呼ばれています。

思いがけないところで $\sin$ 、 $\cos$ 、 $\log$ が出てきました。これは簡単には手計算できないぞ、手計算諦めよう、とも考えましたが、コンピュータのなかったリーマンの時代でも数表と呼ばれるものがあり、代表的な関数の値を数表から得ることができます。過去に数表を作ってくださった方々に多大な敬意を払いつつ、発表を続けます。

f:id:mattyuu:20161002134253j:plain
↑
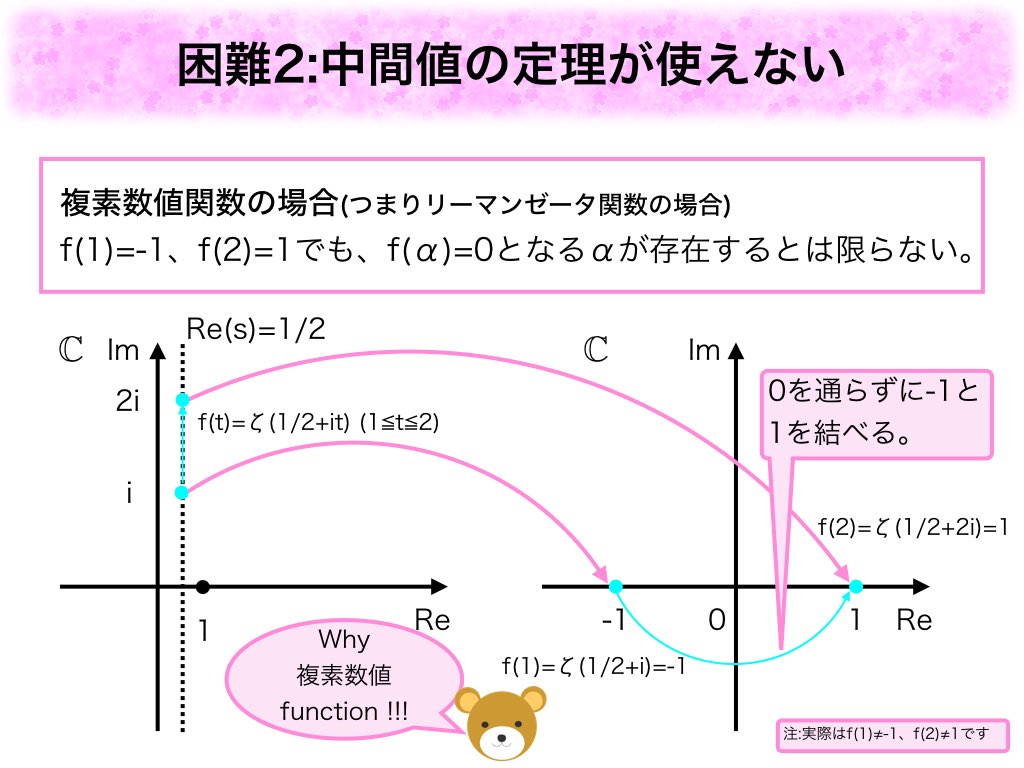
次の困難は複素数値関数であるリーマンゼータ関数では中間値の定理が使えないことです。私はあまり数値計算法に明るくはないのですが、中間値の定理は関数のゼロ点を求めるために、とても重要なものであろうと容易に想像がつきます。例えば上の例のように $f(1)=-1$ 、 $f(2)=1$ であれば、 $x$ が $1$ から $2$ まで増加する間にその符号が変わっているため $1<\alpha<2$ となる $\alpha$ が存在して、 $f(\alpha)=0$ になるでしょう。 $f(1)$ 、 $f(2)$ の符号が異なるだけで、ゼロ点が存在することを知ることができるのです。

f:id:mattyuu:20161002134302j:plain
↑
しかしリーマンゼータ関数は実数値関数ではなく複素数値関数です。実数と違い複素数は2次元の平面と同一視できます。2次元の複素平面上では $-1$ と $1$ を $0$ を通らずに結べるため、上記の例のように $f(1)=-1$ 、 $f(2)=1$ であっても、 $f(\alpha)\neq 0$ ( $1<\alpha<2$ )ということも考えられるのです。

f:id:mattyuu:20161002134308j:plain
↑
そこで登場するのが、ジーゲルの $Z$ 関数です。複素数値関数で中間値の定理が使えないのであれば、実数値関数にしてしまおうという考えです。ここで細かく説明はできないのですが、 ${\rm Re}(s)=1/2$ 上で、 $Z(t)$ と $\zeta(1/2+it)$ はその絶対値が一致します。つまり、
$\displaystyle Z(t)=0 \Longleftrightarrow \zeta(1/2+it)=0$
が成り立つのです。複素数値関数で中間値の定理が使えない困った $\zeta(1/2+it)$ ちゃんのゼロ点を計算する代わりに、実数値関数の $Z(t)$ のゼロ点を計算すれば良いということです。これも大きな進歩です。

なお、この $Z$ 関数にはジーゲルの $Z$ 関数と名付けられておりますが、その存在はリーマンが論文に書いていた関数等式から初等的に導出することができます。また、ジーゲルより前の時代のグラームがゼロ点の計算に用いていることから、ジーゲルはこの関数の発見者ではないと思われます。ジーゲルがリーマンのメモを解読する中で何かこの関数に重大な意味づけした等の功績で名前が付いているものと私は考えております。

f:id:mattyuu:20161002134315j:plain
↑
$Z(t)$ の計算のために必要な $\theta(t)$ もガンマ関数のGaussの公式、
$\displaystyle \Gamma(s)=\lim_{N\rightarrow\infty}\frac{N!N^s}{s(s+1)\cdots(s+N)}$
やオイラー・マクローリンの和公式を用いることで上記のように近似計算ができます。実際にはその後 $e^{\theta(t)}=\cos{\theta(t)}+i\sin{\theta(t)}$ を計算しないといけないのですが、数表を使えばなんとかできそうです。

f:id:mattyuu:20161002134320j:plain
↑
ついに武器は揃いました。 $t$ に対して、オイラー・マクローリンの公式から $\zeta(1/2+it)$ を計算し、その後 $Z(t)$ を計算します。いくつかの $t$ に対して $Z(t)$ を計算して、例えば $Z(t_1)<0$ 、 $Z(t_2)>0$ であれば、複素平面上で $s=1/2+it_1$ と $s=1/2+it_2$ を結ぶ線分上に $\zeta(s)=0$ となるゼロ点が存在するのです。

f:id:mattyuu:20161002134326j:plain
↑
今回はコンピュータのなかった時代にどうやってゼロ点を計算したのかを知りたいため、実際に計算する前に上記のルールを策定しておきます。

f:id:mattyuu:20161002134331j:plain
↑
こちらが私が実際に計算した $t$ になります。最初は $t=1,2,3,4,\cdots,20$ と計算していこう、その後符号が変わったあたりを $t=X.1,X.2,\cdots,X.9$ と計算していき
とゼロ点をそれなりの精度で求めたかったのですが、実際にやってみるとその大変さからたった3つの $t$ に留まってしまいました。。。

なお、それぞれの $t$ に対して、 $M$ 、 $k$ を上記のように選べば、その誤差を $10^{-5}$ 程度まで小さくすることができます。

f:id:mattyuu:20161002134337j:plain
↑
計算結果をお伝えする前に白状しないといけないことがあります。計算を進めている中で突然のルール改定が行われました。計算を続け大量の筆算で嫌気がさしてきた頃に、急遽 $45.9727÷101$ が現れました。「 $÷100$ にしたいよ、 $÷101$ とほとんど結果一緒でしょ、、もう嫌だ電卓使っちゃおう」という流れでルール改定を決心しました。電卓を使っていいと言っても1ステップの計算に限ります。そこは譲れません。

「昔の人は偉いな、すごいな。自分たちは便利なものに囲まれて何か大事なものを見失っている気がする。」そういう風に思いました。

f:id:mattyuu:20161002134344j:plain
↑
こちらが最終結果になります。 $\zeta(1/2+it)$ 、 $Z(t)$ それぞれに対して、私の手計算の結果と、Wolframというアプリで計算した正確な値を比較しております。自分でも驚くほど計算結果が近いものになっておりました。面白いと感じたのは $Z(t)$ は実数値関数になるため、私の手計算の結果の虚部もかなり小さい値になっていたことです。

計算時間に関しては $t=5$ の途中で突然のルール改定が行われたため、 $t=10$ 、 $t=15$ に対しては計算時間が短くなっております。

$Z(10)<0$ 、 $Z(15)>0$ となっていることから、 $10<\alpha<15$ となる $\alpha$ が存在して、 $\zeta(1/2+i\alpha)=0$ となる非自明なゼロ点が存在することがわかりました！！！！

今回はこれ以上精度を上げて計算はできませんでした。。。
今回はと書きましたが、今後もやりません。こんな計算はコンピュータを使えば一瞬です。便利なものは使います。

f:id:mattyuu:20161002134355j:plain
↑
計算をしていて気づいたことは私の計算用紙とリーマンの計算用紙の見た目がなんとなく似ているということです。リーマンという知の巨人に少し近づけた気がしました。

f:id:mattyuu:20161002134401j:plain
↑
こちらは今回大変参考になった参考文献になります。私が使った式は全てこの参考書からの引用です。

f:id:mattyuu:20161002134409j:plain
↑
お読みいただきありがとうございました。

最後にちょっとした感想です。

実は虚部が一番小さい非自明なゼロ点は $s=1/2+14.1\cdots i$ 程度になるのですが、最初のゼロ点が私たち人類が日常的に手の届く範囲に存在していることは奇跡ではないかと思いました。最初のゼロ点の虚部が $14$ 程度である必然性はありません(少なくとも私は知りません)。ということは数学の神様がいたずらをして例えば最初のゼロ点が $1/2+10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000i$ であれば、コンピュータを使って計算を続けても非自明なゼロ点を1つも見つけられないということがあり得たのではないかと思います。非自明なゼロ点を具体的に1つも挙げられない中、全ての非自明なゼロ点が一直線上に並んでいることを証明するのは相当心が参るのではないかと。