ロマ数ボーイズ～フォトアルバム～

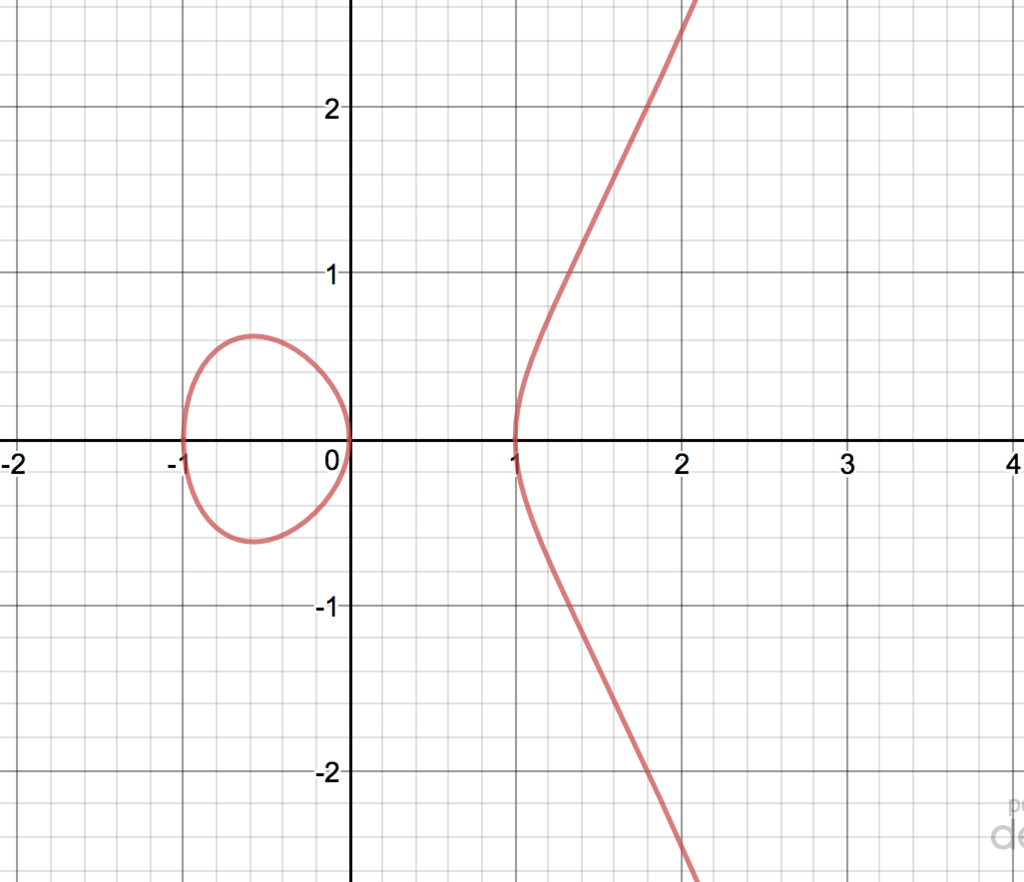
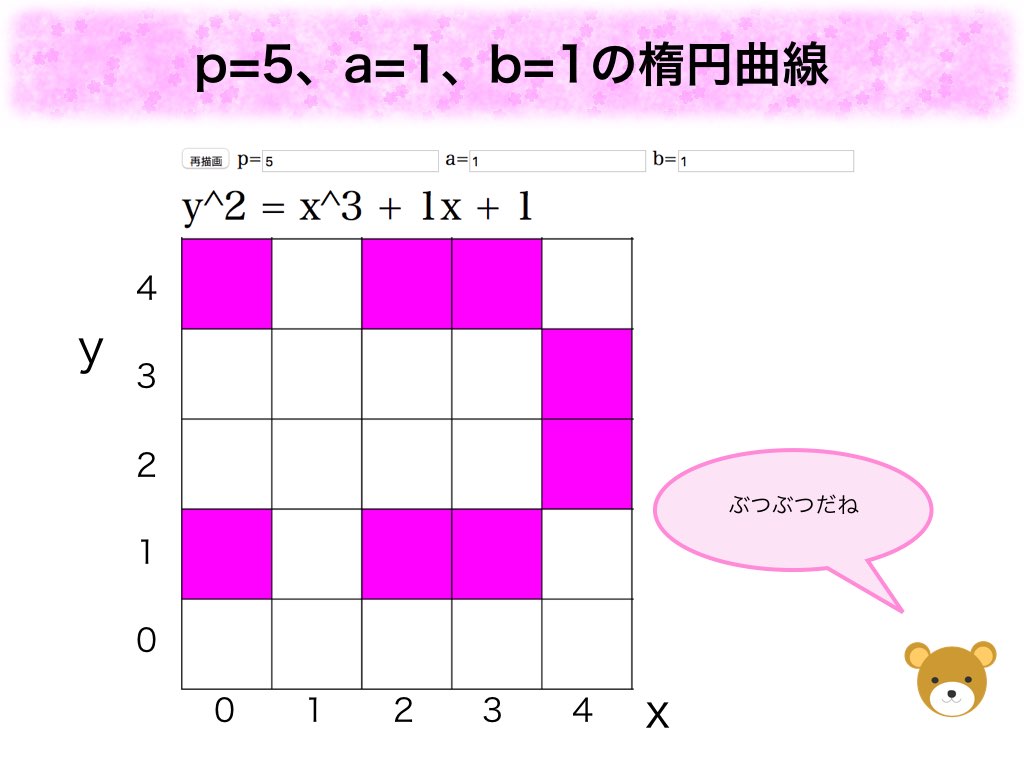
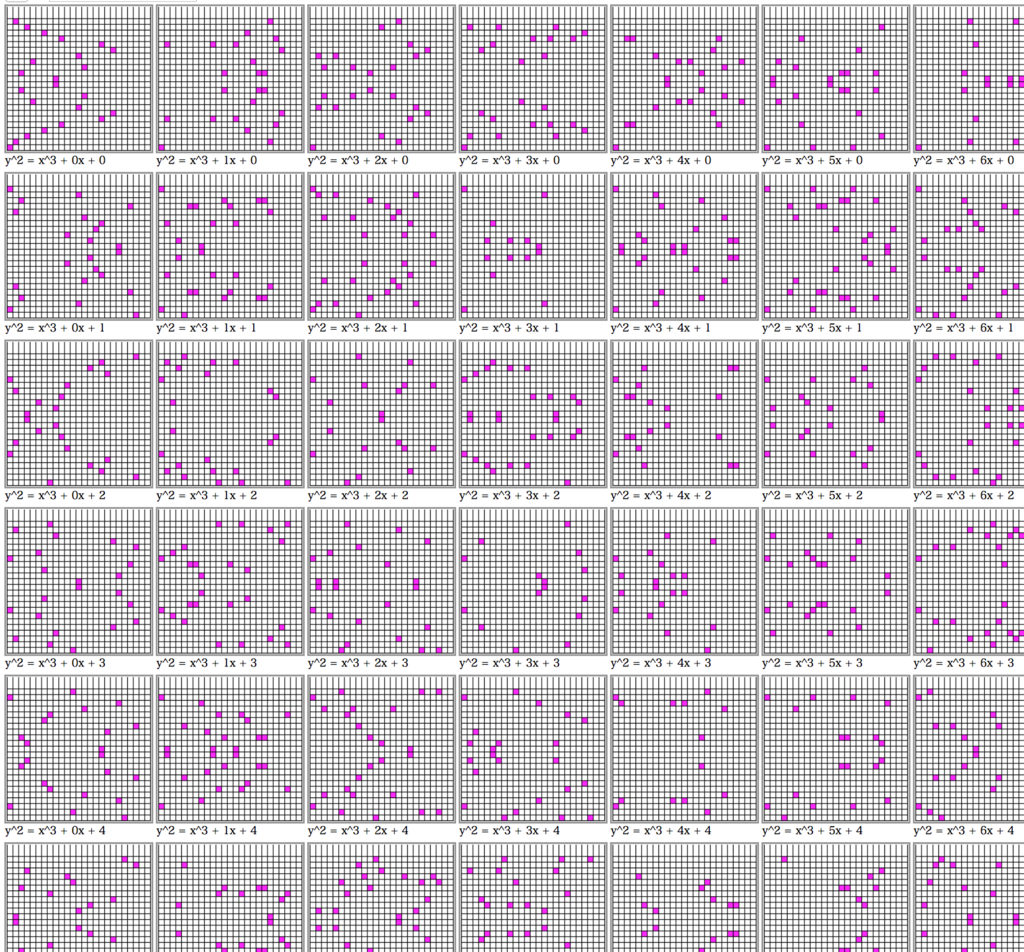
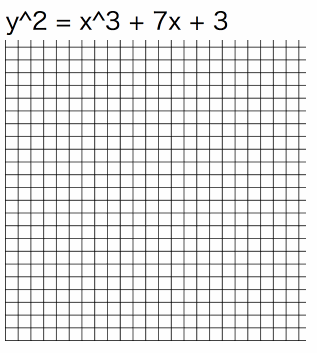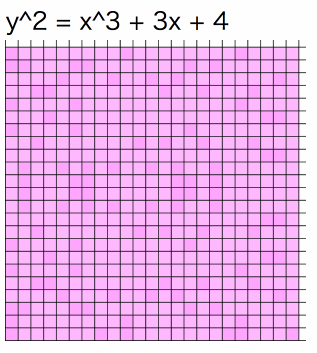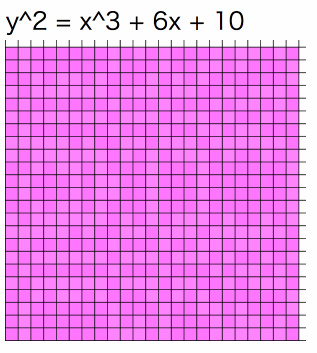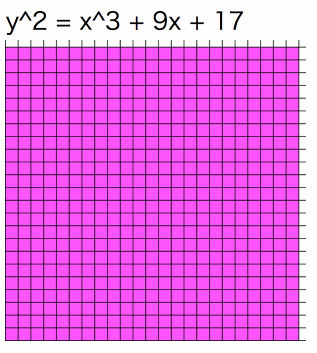
はじめに

2017年4月1日に「【非公式】ロマンティック数学ナイトボーイズ(以下、ロマ数ボーイズ)を開催しました！当日の様子をフォトアルバムのような感じでレポートします。40枚超えの画像ファイルが貼られておりますが、1ファイル当たり50KB〜100KBに抑えましたのでご安心ください。写真を撮っていただいたHF(仮)(@prinum2357)さんありがとうございました。

当日の様子に関しては、この業界で有名なもっちょさんが当日のtwitterのまとめもしてくださっています。臨場感溢れるtweetによる実況も是非楽しんでください。

togetter.com

なお、同日同時間帯に和から株式会社様主催の【公式】の「ロマンティック数学ナイトガールズ」も開催されていました。ロマ数ガールズのレポートは下記にまとめられておりますので、ぜひご覧になってください。

wakara.co.jp

ロマ数ボーイズ開催

司会はソニーミュージックアーティストでお笑い芸人をされているセントラルパークの倉重かおるさん(以下、かおるさん)です！

「ロマンティックでも、ナイトでも、ボーイズでもない。あっているのは数学だけ」と言う開会宣言でロマ数ボーイズが開催されました。

かおるさんは数学好きが集まるイベントがあるとは信じれなかった、エイプリルフールの嘘ではないかと思っていたようです。。。

1.コロちゃんぬさん

〜食べられないパンと数学〜

トップバッターは普段高校の先生をされているコロちゃんぬさんです。

「パンはパンでも食べられないパンはなーんだ？」という定番のなぞなぞに対して、数学的な解を与えてくれました。

随所に数学ワードに関連付けたオヤジ顔負けのオヤジギャクを披露する笑いの絶えないプレゼンでしたwwwこんなに楽しく数学が学べるなんて、コロちゃんぬさんの生徒が羨ましいですね。

【コロちゃんぬさんの当日資料はこちらからご参照ください】

食べられないパンと数学 from Corochanne コロちゃんぬ

www.slideshare.net

2.怪傑ギリジンさん

〜木を生やそう〜

2番手は現役高校生のギリジンさんです。

木の話？と思いきや数学の基礎論である公理論的集合論のお話でした。「アロンシャイン木」、「王(Konig)の補題」、「ススリン木」、「構成可能宇宙」、「ダイヤモンド原理」初めて聞く用語ばかりでしたが、それぞれの言葉にインパクトがあり、不思議な魅力を感じました。。。。「なんかすごそうだぞ」という小学生のような感想をtweetしてしまいました。。。

プレゼンの参考にされたという『キューネンの集合論*1』を購入したので、次ギリジンさんにお会いする時までには少しでも話せるようになりなりたいと思います。

プレゼン後「ロマンティックは？」とかおるさんに聞かれていました。。かおるさんのロマンティックいびりが始まった瞬間でしたww

3.tsujimotterさん

〜ロマンティックな９つの数について〜

3番手は日曜数学者の生みの親であるtsujimotterさんでした。

ヘーグナー数という虚二次体の類数に関する9つの数のお話です。「1、2、3、7、11、19、43、67、163」はヘーグナー数という性質を持つからこそ、素数をたくさん生成する多項式を生み出したり、ほとんど整数となるような数を生み出したりできます。

カメラ目線ですごくいい笑顔です(^^)数学に限らず好きなことを語る人達の笑顔は本当にいいものですね。今思えばこういった笑顔を見たいからこそロマ数ボーイズを開催したんだと思います。

かおるさんのロマンティックいびりに対して、答えるtsujimotterさん。かおるさんに伝わりきらなかったようで、残念そうな顔で席に戻っていくtsujimotterさんの姿を私は見ました。実はこの後の飛び込みプレゼンでtsujimotterさんが再登場します。乞うご期待。

【tsujimotterさんの当日資料はこちらからご参照ください】

ロマンティックな９つの数 #ロマ数ボーイズ from Junpei Tsuji

www.slideshare.net

4.ぼくけんくんさん

〜ボーイズは分解がお好き！〜

4番手はぼくけんくんさんです。

ボーイズは機械の分解が好きということで、数学における「分解」をいろいろ集めて報告してくださいました。「分解」という単語で数学的な手法、対象を見てみると、素因数分解、フーリエ展開、ホモロジーといった普段バラバラに考えているものたちに何かのつながりが見てきます。「分解とかけまして〇〇(ある数学の用語)とときます、その心は、□□なんです」みたいにこじつけでもいろいろ遊んだら楽しそうです。

「有休はホモロジーの境界作用素のように再来年には消えてしまいます。」という言葉で会場が湧きました。

5.蝶番さん

〜結晶と空間充填〜

歓談タイムを挟んでの5番目は蝶番さんです。

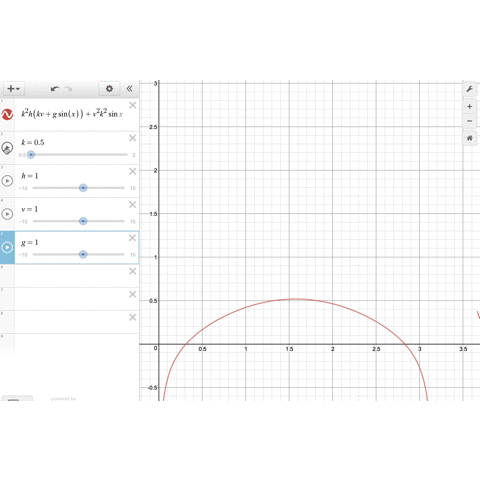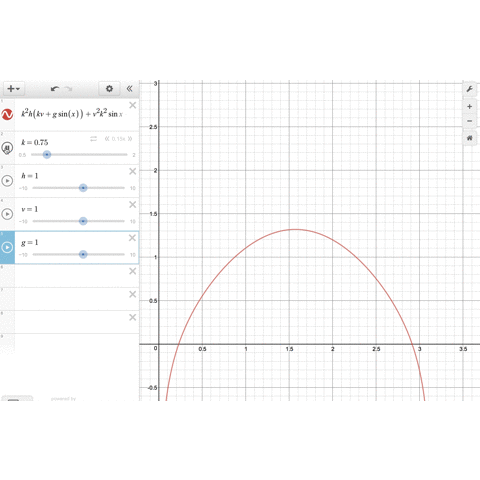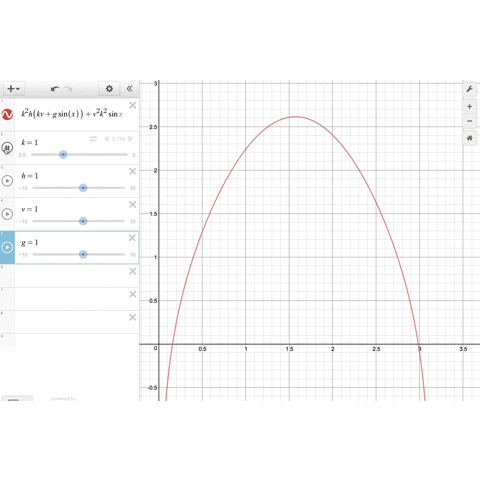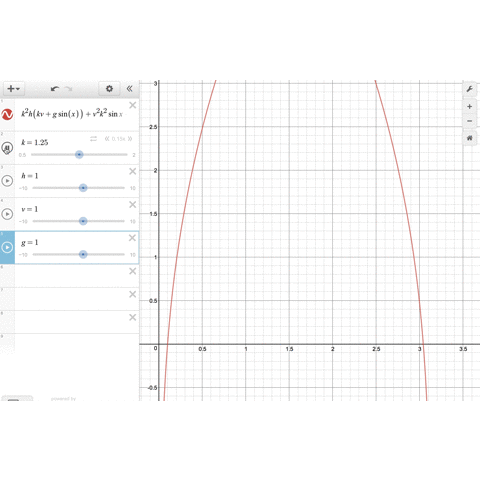
空間を充填する多面体の話です。結晶の格子点は規則正しく並んでいるので、各格子点を起点に3次元のボロノイ図を書けばたしかに空間を充填する多面体ができそうだと納得しました。

蝶番さんのプレゼンのすごいところは3次元を表現したアニメで視覚的に理解できるようにしてくださっているところです。おそらくGeoGebraというソフトを使われております。最近twitterでもたくさんの数学アニメを作られています。私もやってみたい。

歓談タイムの時には空間を充填する少しいびつな多面体の実物を持ってこられておりました。

6.ちゃんおぎさん

〜ロマンティックなので、〇距離恋愛について語ってみる〜

6番手はちゃんおぎさんです。毎週火曜に神保町のみらい研究所で行なわれている「3Dプログラミングのための数学勉強会」でお世話になっております。

レイマーチングという3Dプログラミングの手法で、立体のハートを描いています。ハートの描画には日常私たちがイメージするユークリッド距離を用いています。しかし数学は自由です。距離に関してもある特定の条件を満たせば数学的に距離と呼んでよく、ユークリッド距離以外の距離を用いるとハートはどのような形になるのか？といったお話です。

こんな感じになりました。詳しくはちゃんおぎさんの記事にて動画でご確認ください。
プレゼン中に距離を変えるところだけライブコーディングしたところが私の中では斬新でした。

一般的な意味でのロマンティック成分は十分にあったためか、かおるさんによるロマンティックいびりはなく、逆に褒められていたように記憶しております。

【ちゃんおぎさんの当日発表内容はこちらからご参照ください】
qiita.com

7.三好さん

〜パズルの母はメタパズル～図形パズルのコンセプトデザインについて～〜

7番手は「総務のおじさん」という自己紹介でお馴染みの三好さんです。

三好さんがコンセプトを提案されたGrowing Mirror Symmetryというパズルについてお話をしてくださいました。どのようにコンセプトが生まれたのか、またコンセプトからどういった過程でパズルが出来上がったのかといった話をメタパズル、メタメタパズルという用語を用いて説明されました。

パズルが出来上がるまでの過程を見ずに、出来上がったパズルだけを目にする機会の多い私たちは、「どうやってこんなパズル思いつくんだよ？」とパズル作成者と自分の能力の差に悲観的になってしまいがちですが(少なくとも私は)、大事なのは「図形の不思議に気づくこと」、「パズルを愛する仲間たちとの交流」とのことです。これはパズル作成に限った話ではないなと思いました。常にアンテナを伸ばしておき、同じものに感動できる仲間たちと話すことで、すばらしいモノを生み出すことができるのではないでしょうか。

最後突然Romantcというスライドでプレゼンが終わったため、

当然ロマンティックいびりが始まりましたwww

歓談タイムでは参加者の方がGrowing Mirror Symmetryを実際に触っておられました。

8.s.t.さん

〜TDAしnight!!〜

8番手はロマンティック成分はないと最初に断っておいたs.t.さんです。

Topological data analysisという分野のお話です。

いつもたくさんの数式を超スピードで発表されるs.t.さん。今回はこのような絵のスライドもあり説明が丁寧だと言われていました。persistent homologyという道具を使っているようなのですが、私には難しいかったです。ただ楽しそうに話すs.t.さんを見るのは好きです。

歓談タイムではガチな話をされておりました。

9.みうらさん

〜4階と5階のあいだ〜

二回目の歓談タイムを挟み、9番手は現役大学院生のみうらさんです。

スタイリッシュに、安定の語り口でプレゼンをしてくださいました。カタラン予想を語りつつ、n/(n+1)、(n+1)/nが共に有限小数になるのはn=4の時のみであることが示されました。

有限に思いを馳せる。ロマンティック成分は人それぞれです。かおるさんからは「ロマンティック カムバック！」と褒められていました。

【みうらさんの当日資料はこちらからご参照ください】

4階と5階のあいだ from K. Miura

t.co

10.nkjmゆうさん

〜「もんもん」とした生物多様性を計算する〜

10番手は生物学の分野から登場のnkjmゆうさんです。いつも生物学の話に数学を織り交ぜてプレゼンしております。

「目に見える生物はあんまり興味ない」ということで、細菌がお好きのようです。生物の種類の分類の階層に「門」というものがあるようで、「細菌の世界にはどれだけ門があるねん？」という問題に数式を使ってった話のようです*2。

細菌は目に見えないだけですごく多様ってことです。

11.小清水さん

〜2進数フレンズ〜

11番手は小清水さんです。

話題のけものフレンズを題材に2進数の世界の話です。けものフレンズの主題歌を歌おうとしましたが、歌詞を忘れてしまったようで失敗しましたwww

コンピュータでは2進数で数が表現されていて、2進数で表現しているからこそ起こる不思議な現象を紹介されました。また負数の表現の話のところは、加藤文元先生のp進数の入門書でも同じような話が出てきており面白かったです*3。

やはりまとめで突然のロマンティック成分www
この後かおるさんのロマンティックいびりが始まったのは言うまでもありません。誤解のないように言っておきますが、かおるさんはロマンティックいびりをしつつ会場を盛り上げてくださっています。さすがプロのお笑い芸人さんは違います。

【小清水さんのプレゼン内容はこちらからご参照ください】
t.co

12.mattyuu

〜書を捨てよ町へ出よ素数を見つけよう！〜

最後は私のプレゼンです。

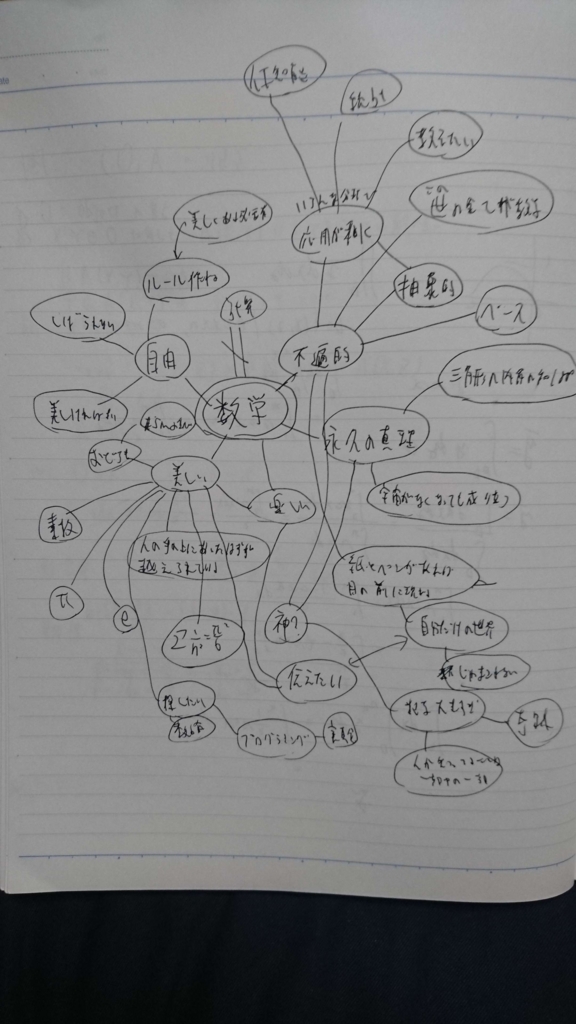
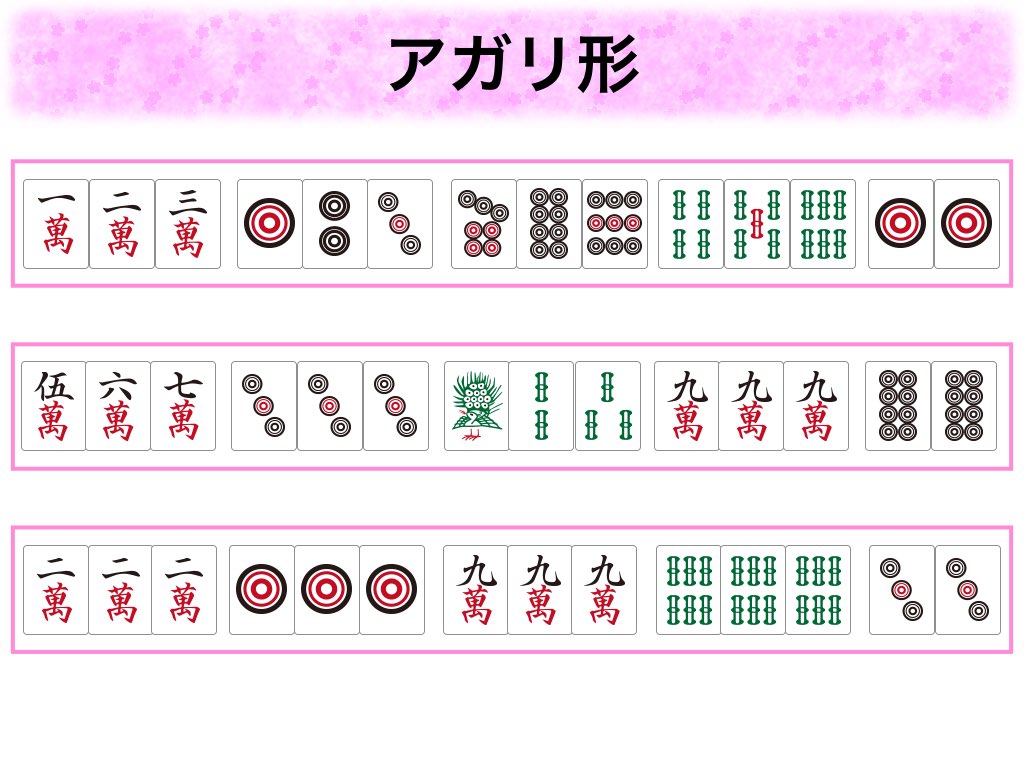
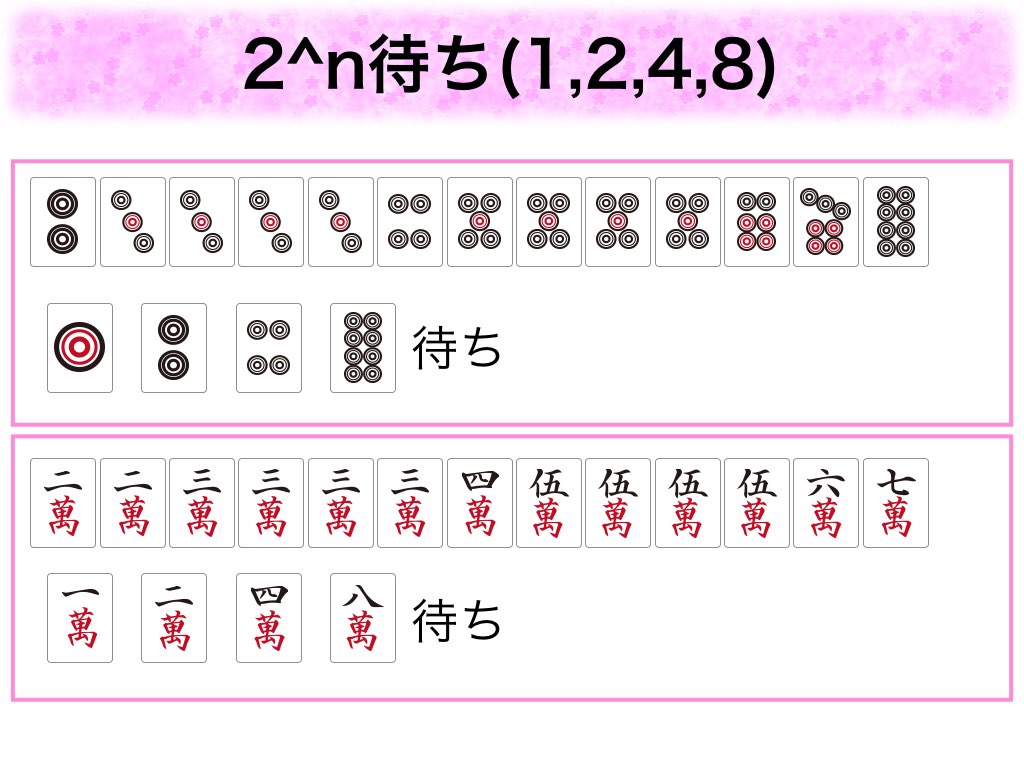
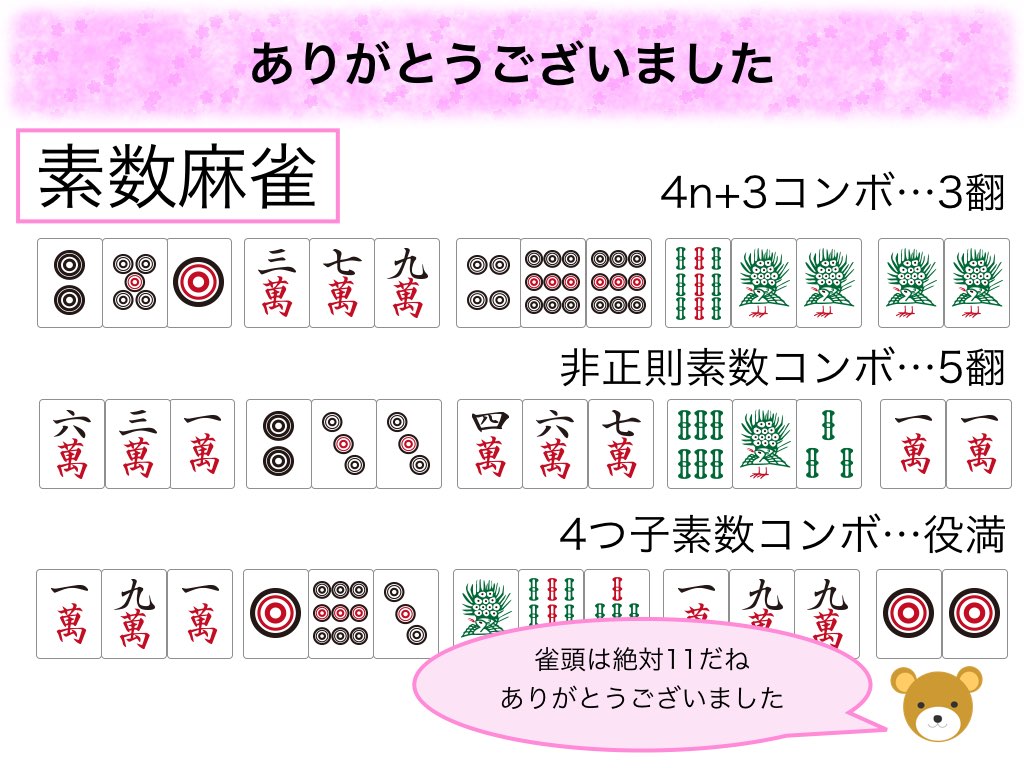
今年も素数が熱いぞということで素数に関するプレゼンです。最初の自己紹介のスライドの辺りの発表は緊張していたのですが、素数の話を始めた時から急に緊張が消え、自分の声をたくましく感じる瞬間がありました。不思議な体験でした。

「素数コレクター！」という街中で素数を集めるAndroidアプリを開発し、その紹介をさせていただきました。

歓談タイムで参加者の方が紙に書いた3つの素数も、

ばっちり素数としてコレクトすることができました。ちゃんと動いてよかった。。。

【素数コレクター！のプレゼン内容はこちらからご参照ください】
mattyuu.hatenadiary.com

飛び込みプレゼン1 tsujimotterさん

飛び込みプレゼンお一人目は「補足スライドが本編」とおっしゃるtsujimotterさんが再登場です。

j関数、虚数乗法という数学用語を用いて、本編の発表では伝えきることができなかったロマンティックに関して語ってくださいました。プロの数学者とアマチュアの数学好きの間には壁、ギャップがあるように感じますが、実はそんなことはなく、私たちの目の前に現れる不思議な現象(今回の例では本編の素数を生成する多項式やほとんど整数の話)の背後に、陸続きで昨今のプロの数学者の研究が繋がっているのです。というお話でした。

数学それ自体がロマンティックだと語るtsujimotterさん。確かにそうでした。ロマ数ボーイズではプレゼンにロマンティック成分を入れるように頼んでおりましたが、そんな必要は全くなかったということを認識した瞬間でした。

自分が好きな「ロマンティックな数学」の話を熱く語る、これ以上ロマンティックなことがありますでしょうか(いや、ない)。

飛び込みプレゼン2 宮永さん

飛び込みプレゼンお二人目、そして最後のプレゼンターは宮永さんです。

九連環という知恵の輪の解法が、

なんと紙を半分に折っていくときの山折り、谷折り、紙が下か、上かといった情報と1:1に対応するとのことです。数学の魅力として、異なる分野で思いもよらないつながりが発見されるということがありますが、まさにその例だと思いました。

tb_lbさんからの挑戦状

参加者の方には、tb_lbさんからの数学の問題3題を配布しました。tb_lbさんはMathPowerへの良問の問題提供で話題を集めたお方で、お忙しい中突然のお願いに対して快く問題を作っていただけました。どれもこの上なく面白いです。私は問題2が好きです。驚くべきことに問題や解答が開催日4月1日の4、1に絡んでいます。こちらにも貼り付けますので、まだ解いてない方はぜひ挑戦してみてください。

【問題１】

【問題２】

【問題３】

さいごに

なんと！何らかのトレンドのランキングで、同日にセンバツ決勝を決めた"大阪桐蔭"に続くトレンドワードとして"#ロマ数ボーイズ"が2位にランキングすることもできました！盛り上げてくださったみなさんありがとうございました！

今回イベントが成功したと言っても良いのは、司会のセントラルパーク倉重かおるさん、問題提供をしていただいたtb_lbさん、プレゼンターが定員に達さず突然のお願いにも関わらず快くプレゼンターを引き受けてくださったプレゼンターの方々、会場が狭いのに文句を言わず楽しんでくれた参加者の方々、事前準備、当日準備を手伝ってくれた幹事グループの皆さん、ボーイズと名乗ってイベントを開催することを承認してくださった和から株式会社様のおかげです。本当にありがとうございましたm( )m

最後に記念撮影です。みんないい笑顔です(^_^)

*1:

集合論―独立性証明への案内

*2:私の席からはnkjmさんのスライドが見えず、自分のプレゼンも迫っていて心に余裕がなく、ゆっくり見れてません。。すみません。誰か補記できる方はご連絡ください。。。

*3:

天に向かって続く数

書を捨てよ町に出よ素数を見つけよう！

はじめに

2017年4月1日に「【非公式】ロマンティック数学ナイトボーイズ(以下、ロマ数ボーイズ)*1」という数学イベントを主催し、私も掲題のタイトルでプレゼンを行いました。当日の様子は近いうちにレポート形式で公開しようと思います*2が、まずは私のプレゼンの内容を公開します。イベント開催日もブログ公開日もエイプリルフールである4月1日ですが、本記事の内容に嘘はないことは明言しておきます。

なお、「ロマ数ボーイズ」の開催宣言は私の素数記念日に行っています。

2017年(平成29年)2月7日31歳の誕生日

2017,29,2,7,31 素数が並ぶ記念日にこのようなイベント開催の通知ができて嬉しいです(*^^*)(*^^*)(*^^*) https://t.co/91Oza1aej2

— mattyuu (@mattyuu123) 2017年2月7日

また、私が初めて公の場で数学の発表を行った2016年10月1日の第7回日曜数学会「リーマンゼータ関数のゼロ点を手計算してみた*3」のプレゼンからちょうど半年ということで、いろいろな意味でとても感慨深いイベントとなりました。この半年間で今まで付き合ってこなかったような方とたくさん知り合いになれました。今後ともよろしくお願いします。

また、今後出会うであろう数学好きの方、数学好きになりそうな方、数学嫌いでも必要だから学ぼうとされている方、今後よろしくお願いします。

2018年4月13日追記)
素数コレクターを本家のロマンティック数学ナイトでもプレゼンしました。その時の様子がYouTubeで公開されておりますので、是非ご覧ください。

20170701ロマ数⑧素数と戯れよう(松中プレゼン)

では始めます。

みんな大好き素数

というのは言い過ぎですが、少なくとも数学好きの方の中には素数好きは多いです。「ホテルの部屋番号が素数！だった！」とか、「AKB48の総選挙のさっしーの得票数が素数だ！」というようなツイートを見かけることがありますし、今年「素数大富豪*4」はメディアにも取り上げられ今まで数学を意識していなかった多くの方がその存在を知るところになりました。また、先日は素数姫さんが「素数に恋する女*5」という本を発売するなど数学界は素数の話題に事欠きません。

かく言う私も素数が好きです。居酒屋の靴箱の番号や駐輪場の駐車番号では必ず素数を探し、靴を入れ、自転車を止めています。アパートの部屋番号も301、素数です。

こんなツイートもしています。

日帰り温泉に行きました。
傘立ての番号、下駄箱の番号、荷物ロッカーの番号、着替えのロッカーの番号、それぞれ素数にしないといけないというハンデを背負ってるので、一般の人に比べて不利だなと思いました(*_*)#何が

— mattyuu (@mattyuu123) 2017年2月20日

数学者、数学好きの方が素数を愛する理由は様々なものが考えられますが、私が一番の理由と考えるものは「無秩序の中の秩序」という言葉で表せます。数学者は様々なものを観察し、そこから共通のパターンを抽出し、一般化、抽象化して強力な理論を組み立てます。そういった意味で数学者はパターンを探す天才です。そして古くから知られている対象であるのに数学者がそのパターンを見出せない存在、それが素数なのです。

素数は多くの天才数学者からの「お前を制御したい」というアプローチをひょいとかわします。それほど素数は無秩序です。しかし無秩序であると考えられてきた素数が、実はある側面では驚くべき秩序を兼ね備えていることを数学者達は歴史を通して発見してきました。ここでは私が特に「秩序ってるなぁ」と思う3つの数式、定理を言葉だけで簡単に紹介します。(わからなくても本記事には関係ないので気にしないでください)

これほどまでの驚くべき秩序を兼ね備えながら、今の所出現が予測できない無秩序な素数、、、やばいですよね。。。

「素数コレクター！」概説

というわけで、まとめると数学好きの方は街中で素数を探してしまうんです(少なくとも一人はいます。私です。)。でも街中の素数との出会いは一期一会。わざわざどこでどんな素数に出会ったかなんてめんどくさくて記録できません。それでも素数との出会いを大切にしたい。。。悩める日々の中で私が思いついた解決策、それが「素数コレクター！」の開発でした！

ジャジャーン！

(トップページの画面右下くまさんの顔をタップすると次の画面に進みます。#BAD_UI)

「素数コレクター!」は私が開発したAndroidアプリです*6。このアプリは、街中で撮った写真から素数を自動で抽出し、自分だけの素数図鑑に登録してくれます。素数との出会い日記帳を作るイメージです。素数好きの方にとったら、まさに夢の素数アプリではないでしょうか。メイン機能としては「素数コレクト!」、「素数図鑑」、「ステータス」の3機能があります。次章から1つずつ紹介していきます。

「素数コレクト!」機能

これがまさに「素数コレクター!」の肝となる機能です。トップページからの初期遷移時は下記のような画面になっています。

[画像選択]ボタンを押して過去にとった写真を選択する、もしくは[カメラ起動]ボタンを押して写真を撮ると、下図のように写真が画面に表示されます。(下の例は私が過去にRSA暗号について語った時のプレゼン資料をカメラで撮ったものになります。)

さあ、この状態で[素数コレクト!]ボタンを押しましょう。白黒のテキスト写真であれば数秒で、今回の例のようなカラフルな写真であれば10秒程度で素数抽出処理が完了し、下の図のように写真内の数と素数がそれぞれ抜き出されます！

確かに"5"、"29"と素数が抽出されていることがわかります。しかし"27"はどこにあるのでしょうか？実はわかりにくいですがこの画像ファイルの左上に"27.jpeg"というファイル名が表示されています。ここから"27"が抽出されたのです!なんかすごくないでしょうか？*7

とは言っても、この写真ファイルからテキスト情報を抜き出す処理はGoogleのWeb API*8を使っています。この処理の部分は私が開発したところではないことを明言しておきます。さすがGoogle様。貴方のおかげで「素数コレクター!」が作れました。ありがとうございます。

一点補足すると例えば"7253"という数字列があった時、「素数コレクター!」では"7"、"2"、"5"、"3"や"53"といった素数はコレクトせず、あくまで"7253"という素数のみをコレクトするようにしております。また"2,200円"と記載された広告を写真に撮ってコレクトした場合は、"2"と"200"を写真内の数字列として分けて取り込み、結果"2"が素数としてコレクトされます。

こうして抽出された素数"5"、"29"は素数図鑑に記録されます。次の章では「素数図鑑」機能を紹介します。

「素数図鑑」機能

さて「素数コレクト!」画面で画面左部分を画面外から画面内にスワイプすると、下図のようにメニューがするーっと現れます。

ここから別の機能に遷移することができます。では「素数図鑑」メニューをタップして素数図鑑を見てみましょう。

「素数図鑑」画面では今までに「素数コレクト!」機能で見つけた素数が登録されます。リスト形式になっておりスワイプすることでより大きな素数も見ることができます。

しかし、これでは見出しがあるだけで図鑑にはなっていませんね。安心してください、これでは終わりません。では今回見つけた"5"をタップしてみましょう。

なんと"5"の詳細ページに飛び、画面下部にはWikipediaのページが現れました！スワイプすることで"5"に関する様々な情報をWikipediaから学ぶ事ができます。

さて画面上部には"5"を今まで何個見つけたかも表示されています。そして、その横には[生息地確認]ボタンをいう気になるボタンがあります。早速タップしてみましょう。

なんとGoolge マップの画面が現れ、これまでに自分が"5"を見つけてきた場所にピンが打たれているではありませんか！これで"5"さんとの思い出の場所を覚える必要がなくなりますし、"5"さん以外の別の素数さんとの思い出と"5"さんとの思い出が混ざってしまって、"5"さんと微妙な関係になってしまう事も防げそうです。

、、、

というわけで、最後に「ステータス」機能を紹介します。

「ステータス」機能

「ステータス」機能は今までの機能とは違いとてもライトな機能になっており、次の1画面だけでボタン等の利用者が制御できる部品はありません。

ここではこれまでに見つけた、

• 素数の種類
• 総個数
• 最大の素数
• 最多の素数

をそれぞれ確認することができます。画面下部ではくまさんが貴方の素数コレクターとしてのレベルを教えてくれます。

しかし、レベルは素数のコレクト率(=全素数の種類に対する、集めた素数の種類の割合)で算出するようにしております。素数が無限個あることから、何億種類の素数を集めてもそのコレクト率が0%より大きくなることはありません。つまりみんないつまで経っても「見習い素数コレクター」です。素数の前ではみんな平等という勝手なコンセプトを打ち出しているのです。

以上で「素数コレクター!」全体を通しての機能説明を終えます。

ロマンティック成分

このプレゼンはロマ数ボーイズのために用意したものであることを思い出してください。ロマ数ボーイズではプレゼンターの方に、プレゼンにロマンティック成分を入れていただくように事前に頼んでおりました。当然私も「素数コレクター!」を使ったロマンティックなプレゼンをする必要があります。

ロマンティックを演出するために題材として選んだのは、、、、なんと山手線です！

JRの路線図などを見ると山手線は円であるようにデフォルメされていますが、実際はグニョグニョしており、実はハート形に見えなくないのです。

d.hatena.ne.jp

この山手線沿線で素数を探し、その素数の生息地がハート形になればこんなロマンティックなことはないのではないでしょうか。

ということで、山手線沿線で素数を集める旅に出ました。集める素数として選んだのは、自分が見習い素数コレクターであるということも加味して、一番難易度が低そうな"2"にしました。

自分で作ったアプリを片手に素数を集めに町に出る、、、、なんて幸せなことなんでしょう。有楽町でレンタサイクルを借り、反時計回りに山手線を回りながら素数"2"を探しました。

そして素数を探していると、縦書きの数字列も認識するという事実を発見しました。下の図は居酒屋の看板ですが、看板の右後方にひっそりと数字列が存在しています。その数字列が横方向、縦方向それぞれ認識されていることが分かるかと思います。さすがGoogle様です！

慣れない土地で道に迷ったり、自転車だったら歩道橋が使えず途方にくれたり、夜になって素数が見つけにくくなったり、雨が降ったり、寒かったり、、それなりに苦難をのり超え２日間で8時間をかけ"2"を集め、完成したのが次の"2"の生息地です！

ジャジャーン！

ハートのくぼみを顕著に出すために、途中山手線から離れている箇所もあります。また、時間と気力がなく品川の方までは下がれませんでした。細かい話は抜きにしても、これはどっからどう見てもハートじゃないでしょうか。

この素数"2"の生息地をプリントアウトして、高級指輪の箱に詰め、彼女に「君のためにこの大都会東京に素数でハートを描いたよ」と決め台詞を吐けば結婚間違いないでしょう*9。

まさに、ロマンティック！！

余談にはなりますが、池袋、新宿の南側にそれぞれ素数砂漠 *10を見つけたことをご報告させていただきます。

さいごに

さいごに「素数コレクター！」の地域格差及び数学の力について語らせてください。

「都会は看板や建物が多いから素数がたくさんあっていいよね、、、僕の住んでる田舎は田んぼや畑ばっかりで素数なんてちっとも見つからないよ。これじゃポ◯モンGOと同じで地域格差が生まれちゃうよ」と嘆かれてる方もいるかも知れません。

しかし、本質は違うんです！この素数コレクターで集めているものは実は素数ではなく、人間が勝手に作った素数を表すただの記号(数字)の列なのです。本来素数はどこかにあるようなものではなく、また本来素数はどこにでもあるものなのです！

田舎でも紙とペンを用意して紙に"2"という記号を書けばそこに素数(と呼んでいる数字列)が現れます。その"2"を出発点として紙の上でペンを走らせれば、どこにもないはずの世界が、そしてまた驚くほど豊潤な世界がはっきりと広がっていくのです。これが数学の力なんです！都会は表向きは素数が溢れ、田舎には素数がないように思えてしまいますが、それはまやかしです。数学の世界は全ての存在に対して平等です。当然都会も田舎も全く関係なく平等なのです！

スペシャルサンクス

このハートマークを作るための素数集めの旅において街中のいろいろな方にお世話になりました。お世話になった方々へのお礼を記載して本記事を締めくくりたいと思います。お世話になったレベルの高い順にベスト3をランキング形式で掲載します。最後まで読んでいただきありがとうございました。

[第1位]テナントビルの階数表示さん

そろそろ素数が欲しいと思った時、周りを見渡せば貴方がいてくれました。テナントビルは普通二階以上あるので簡単に"2"を集めることができました。本当にありがとうございました。

[第2位]電信柱の住所表示標識さん

例えば何処かの街の二丁目に差し掛かると、出会う貴方は皆"2"を持っていました。ハート形のくぼみのところの"2"を集める時は大変お世話になりました。ありがとうございました。季節の変わり目ですので、くれぐれもお体に気を付けてこれからも頑張って下さい。

[第3位]建築計画さん

上位2名の方に比べたら出会う機会は少なかったですが、貴方にはたくさんの文字列が書いてあります。探せば大抵そこには"2"もあり、貴方は特別な安心感を与えてくれました。ありがとうございました*11。

ちなみにお世話になったランキング第4位は賃貸アパマンの広告さんでした。写真は載せませんが、ありがとうございました。

*1:和から株式会社様主催の公式の「ロマンティック数学ナイト」に対して、個人で勝手に企画したイベントですので【非公式】としております。名称を使う許可は頂いています。同日同時間帯に公式のロマンティック数学ナイトガールズが開催されておりました。

*2:2017.4.3追記 もっちょさんがtogetterしてくださったので、こちらで当日の雰囲気がバッチリわかります。https://togetter.com/li/1096657

*3:mattyuu.hatenadiary.com

*4:下記が素数大富豪の考案者せきゅーん氏の素数大富豪のまとめサイトになります。 integers.hatenablog.com

*5:私も持ってます！

素数姫の素数入門

*6:いつかGoogle play ストアに公開したいです！が、今のところいつになるかわかりません。自分が趣味で作ったアプリが何かの間違いで第三者のAndroidを壊してしまう、といった恐怖もありますし、作り込みが甘いところがあったり、現状ソースが汚かったりすることも理由です(APIの結果のjsonをオブジェクトではなく文字列として扱っているところ、数の抜き出しを正規表現ではなく、ゴリゴリで行っているところなど。自分でソースが汚い、作り込みが甘いと認識できているだけマシとは思いますが。。)。有識者の方にレビューをいただきながらしっかり完成させ公開したいです。

*7:しかし当然ながら素数の抜き出しに100%成功するわけではありません。どんな写真を撮るかで成功率は大きく上下しますが、私が素数を抜き出すために撮った(それなりにちゃんと素数が写っている)写真での成功率は80〜90%くらいという感覚です。大抵撮り直せばちゃんと取り込まれます。取り込まれないものはどんだけ写真を撮っても取り込まれませんでした。この辺りはGoolge様のAPIの進歩で改善していくのではないかと思います。

*8:こちらのCLOUD VISION APIのOCR機能になります。 cloud.google.com

*9:同じようなプロポーズネタを以前の有限体上の楕円曲線のオチとして書いたので、まだ読まれてない方は是非読んでみてください。 mattyuu.hatenadiary.com

*10:2,3,5,7,11,13,,,と素数は無秩序に無限に出現しますが、しばらく素数が出現しない区間を素数砂漠と呼んでおります。実は任意の長さの区間からなる素数砂漠が存在することを中学、高校レベルの数学で簡単に示すことができます。

*11:建築計画の写真を撮る私の姿はあまりにシュールで、周りの方々に建築オタクと思われてしまった可能性があります。建築オタクではなく数学オタクですのでそこんとこよろしくお願いします。

有限体Fp上の楕円曲線'のパズル

はじめに

先日職場の勉強会でRSA暗号、楕円曲線暗号について発表をしました。面白いことに話の全体を通してフェルマー(17世紀のフランスのアマチュア数学者)が登場しました。

• RSA暗号の鍵となる素数の面白い性質としてフェルマーのクリスマス定理(4で割って1余る素数が2つの平方和であらわせるやつ。等) の紹介。
• RSA暗号で平文、暗号文を変換するアルゴリズムの原理の証明にはフェルマーの小定理を使う。
• 楕円曲線はフェルマーがそれと知らず(?)好んで研究の対象にしていた。
• 「楕円曲線はモジュラーである」という谷山–志村予想(の特赦なケース)を証明することでフェルマーの最終定理が証明された。

フェルマーはパスカルと共に確率論を創始するなど、上記の暗号関連の話以外にも重要な仕事を行なっております。フェルマーは17世紀の人ですが、現代社会の根っこの部分に彼が与えた、与えている影響は大きそうです。ただ、今回はこれ以上フェルマーの話はしません。勉強会の資料作成を通して、有限体上の楕円曲線を可視化したのですが(←グラフ書いただけですが)、可視化した楕円曲線を眺めたり、いじったりしているうちに、「パズルとして売り出せるんじゃない?」というような面白い性質を見つけたのでその紹介をしたいと思います。

まず、楕円曲線とは下記で定義されます。

楕円曲線の定義

、を定数とし、方程式

を満たす全体の集合(←グラフと呼ぶ)を楕円曲線という。

注1:この記事では上記の一般形を得るために、標数が2、3以外の体上で考えています。、もの元です。
注2:(右辺のxの3次式)=0は重解を持たないものとします。

中学校や高校で習う関数のグラフは、実数体()という足し算、引き算、掛け算、割り算ができる世界*1の上で考えています。実数上で楕円曲線のグラフを描くと、例えば下記の図のようになります。

、の場合

、の場合

2つ目の、)の例でグラフの描き方を簡単に説明します。

のときは、となりますからです。に赤い点を描きます。同様に、のときもとなるので、、にも赤い点を描きます。

のときは、となるので、です。、に赤い点を描きます。先程と違い、1つのに対して2つのが対応しました。

のときは、となるので、これを満たす実数は存在しません。そのため実数上のグラフではのときは描く点はありません。

をからまで動かしながら、各に対して方程式を満たすを同様に求めてに点を描いていくと、先程の2つ目のグラフになるのです。

有限体上の楕円曲線

楕円曲線暗号では、楕円曲線は実数体()上ではなく、有限体上で考えます。有限体が何かわからない方は以前書いた下記の記事を読んでみてください。

mattyuu.hatenadiary.com

は簡単に言えば集合に適切に足し算、引き算、掛け算、割り算を定義した世界になります。今回の記事では足し算と、掛け算しか使わないため、例としての足し算表、掛け算表を載せておきます。

足し算表

+	0	1	2	3	4
0	0	1	2	3	4
1	1	2	3	4	0
2	2	3	4	0	1
3	3	4	0	1	2
4	4	0	1	2	3

掛け算表

×	0	1	2	3	4
0	0	0	0	0	0
1	0	1	2	3	4
2	0	2	4	1	3
3	0	3	1	4	2
4	0	4	3	2	1

有限体の復習が終わりましたので、実際に上の楕円曲線を描いてみましょう。ここでは例として、、とします。

楕円曲線というのに、グラフは繋がってないし、曲がった感じもしませんが、楕円曲線の定義に反してませんし、描き方も実数体上の時と全く一緒です。実数体ではからまでの無限個のに対して、を求めないとグラフは描けませんでしたが、有限体上では個のに対してを求めればよいことが本質的に異なります。

では実際に上のグラフがのグラフになっていることを確認してみましょう。

のとき、となるので、2乗してになる数求めればよいことになります。上では、、、、より、のときは、となります。よってとのマスにピンク色を塗っております。

同様に例えばのとき、となります。上では、より、とのマスにピンク色を塗ります。

様子が違うのはのときです。このときとなりますが、上では2乗してになる数は存在しません。そのための縦列のセルにはピンク色に塗るセルはありません。これは先述した実数体上の楕円曲線の例で、の解が存在せず描く点がなかったことと同じです。

今回有限体上の楕円曲線はjavascriptでプログラムを作って描画しています。プログラムの良いところは一回プログラムを作ってしまえばパラメータ(ここでは、、)を変えたグラフも容易に描画できることです。手計算、手描きでグラフを作成すると、パラメータを変えるごとに改めて計算を行う必要があります。またを大きくすると計算自体が大変になります。

さあプログラムの利点を活かして上の楕円曲線'を全て描画してみましょう。、はそれぞれの5通りから選ぶことができるので、全部で25通りの楕円曲線'が得られます。

上の楕円曲線'たち

にしても描けます!
上の楕円曲線'たち(出力結果を一部抜粋、実際には通りの楕円曲線'が現れます。)

はぁはぁ、、楽しい。。

ここで一点白状します。上記には楕円曲線以外のグラフも含まれています。楕円曲線の定義の注2で記載しましたが、の右辺のの3次式について、(右辺のxの3次式)=0という方程式を作ると、この方程式は重解を持たないという前提があります。例えば上ではとなり、重解を持ってしまうので、上では楕円曲線ではありません。

しかし、今回考えたパズルは全ての、を対象にしないと成立しません。誠に情けないですが楕円曲線の集合に、楕円曲線とは言ってはいけない上のといった曲線も追加して楕円曲線'という名前で広い範囲の集合を考えます。

気づいた性質

さて、楕円曲線'のグラフを並べてみると気づくことがあります。それは、を固定して、をからまで動かした個のグラフを重ね合わせると全マスがちょうど1回ずつピンク色に塗られるのです！

言葉だけではわからないと思いますので、つまりこういうことです。

つまり、こういうことです。

つまり、こういうことです。

最後の例ではピンク色の部分はセロハンのような素材と思ってください。セロハンを重ねるごとにピンク色が濃くなります。が同じ値の時は各セルが足並みをそろえて濃くなっていく様子が確認できます。

でも、綺麗に成り立ちます。(ファイルサイズが大きくなってしまうので、アニメは途中で止めています。)

はぁはぁ、、面白い。。

とか、とかもっと大きい素数では楕円曲線'のグラフもより複雑になります。複雑なグラフが個あり、それを重ね合わせると綺麗なピンク一色！何かに役立つわけではないですが、数学の力を感じさせられます！

この性質が成り立つ証明は超簡単です。残念ながらこの性質は楕円曲線ではない方程式でも成り立ちますし、もっと言えば体上じゃなく剰余類環上でも成り立ちます。

証明

上の楕円曲線':に対してを1つ固定する。この時、下記2点を示せばよい。

1. に対して、でとなる。
2. のとき、、は共通の解を持たない。

• 1の証明:とすればよい。
• 2の証明:が共通の解とすると、、がそれぞれ成り立つ。辺々を引くと、となり、これは前提に矛盾。

証明はいかにも当たり前ですが、可視化してみないと気づかなかった性質なので、満足感はあります。

応用例

楕円曲線'に関して面白い性質を見つけたので、何か応用したくあります。

まずは、大人向けのパズルとして活躍の余地はないでしょうか。のときは、25種類の楕円曲線'が描かれたカードを用意します。色が塗られていない部分は透過するようにしたいためアクリル板で作成しましょう。25枚のカードから適切に5枚ずつ選んで、それぞれの組で各カードを適切に回転、反転させて重ね合わせることで、ピンク一色のカードの組が5セットできたら成功です。*2

が余裕でできるようになったら、、と難易度を上げていけば素数の数だけ楽しめます！

次に思いつくのは子供向けの絵合せパズルです。2〜3歳の時はを固定して、5枚のカードでくまさんの絵合せをしましょう。

幼稚園に行きだしたら、ゴレンジャーを題材にしましょう。この頃になると25枚あっても大丈夫なはずです。

このように子供の時から素数や楕円曲線'に慣れ親しみ純粋に育った男の子は、プロポーズにもメッセージカードと称して楕円曲線'カードを使用してしまう恐れがあります。

おまけ

今回は有限体上の楕円曲線を可視化しました(←グラフ書いただけ)。可視化すると楕円曲線の方程式を満たす解の個数も一目瞭然ですが、この解の個数がフェルマーの最終定理の証明に深く関係しています。また、この解の個数はハッセ・ヴェイユ境界と呼ばれる、より高度な数学にも関連しています。私はステートメントはなんとなくわかるレベルです。

今回楕円曲線とは何かということに関しては何も触れていません。楕円曲線をgoogle検索すると、やはりtsujimotterさんの記事がwikipediaの次に出てきましたので、ここにも貼り付けておきます。楕円曲線の面白いネタがたくさん書かれています。興味がある方は一緒に楕円曲線の勉強をしましょう。
tsujimotter-sub.hatenablog.com

ついでながら、今回ゴレンジャーのアニメはjavascript、canvasで作成したのですが、画像を回転させるのにこれまたtsujimotterさんの下記の記事が大変役に立ちました。原点を中心としてcanvas全体を回転させるのは簡単にできるのですが、画像を中心として、その画像だけを回転させる方法はネットで調べてもよくわからず、ネットサーフィンを続けているうちに下記の記事に行き着きました。参考にこちらも貼り付けておきます。

tsujimotter.hatenablog.com

*1:数学的には四則ができる世界を体(たい)と呼ぶ

*2:このパズルを売り出すためには解の一意性を証明しておく必要があります。

蔵本予想とは何か? 〜予想紹介編〜

1/7に第8回日曜数学会にて「蔵本予想とは何か?」というタイトルで力学系理論に関するLTをさせていただきましたのでご紹介します。私の不勉強のため今回は蔵本予想の紹介に留まりましたが、近いうちに証明も体得して概説したいと思い、本記事では〜予想紹介編〜というサブタイトルを付けております。

蔵本予想とは同期現象に関する数学的な予想になります。"予想"と書いていますが、九州大学の千葉逸人准教授によって証明されています。今回は蔵本予想の概説を行いたいと思います(不勉強ゆえ間違った記載があるかもしれません。あくまでざっくり蔵本予想がどういうものなのかを知っていただければと思います。)。

まず同期現象とは何かを説明します。多数の蛍が集まっている場面、または、多数のメトロノームを集めた状況(←台車の上に置く等、相互に作用するようにする。固い台の上においてはダメ。)を想像してください。最初はそれぞれの蛍が各々のタイミングで発光し、メトロノームが各々のペースで針が振れているのに、十分な時間が経つとまるで一匹の蛍のように、まるで1つのメトロノームのように発光のタイミング、針の触れ方、ペースが揃ってくることが観測されます。これを同期現象といいます。

youtubeに蛍の美しい同期現象がありましたので、リンクを貼っておきます(開始35秒くらいから同期現象の動画が始まります。)。

www.youtube.com

こういった同期現象を語る数学的なモデルに蔵本モデルがあります。これは京都大学の蔵本由紀教授により提案されたものです。

蔵本モデルは上記のような微分方程式で表されます。3ステップでこの式が意味するところを解説したいと思います。

まずステップ1です。蛍の点滅やメトロノームの針が左右に振れる運動のように、同期現象の元となる単体の運動は周期的な運動です。周期的な運動ということで、質点が一定速度で円周上を回る運動をモデルの出発点としましょう。

このモデルの運動を記述する変数として質点が円周の中心となす角をとります。は時間の経過と共に変化していきますので、変数はまた時間の関数とも思えます。その意味でをとも書きます。

次に回るスピード(自然振動数と呼びます。単位時間当たりどれだけの角度回るかという値です。)をとすると、このモデルを記述する微分方程式は、

となります。

自然振動数が大きければ大きいほど質点が円周を回るスピードが速くなっていきます。は固体によって異なる値を取り得ます。例えば短い間隔で点滅を繰り返すせっかちな蛍のは大きく、長時間かけて点滅を繰り返すのんびり屋の蛍のは(絶対値が)小さくなります。

この微分方程式は簡単に解けて下記のように表せますが、力学系理論ではシステム(系)の状態を微分方程式で表すことが通常ですので、次のスライド以降も微分方程式の形で進めていきます。

ステップ1では1つの質点の円周上の運動を考えましたが、質点が1つでは同期現象を考えようがありません。では、次のステップに進みます。

ステップ2では同期現象を発生させるために質点をたくさん、ここでは個集めます。

質点をN個に変更することに伴い、変数も増やす必要がありますので、添え字を付けてとします。そして自然振動数も固体によって異なってもよいものでしたので、変数に対応する自然振動数ものように添え字を付けて表します。

ステップ2で質点の数を個に増やしましたが、の運動を定める微分方程式にはの運動の自然振動数しか出てこず、は登場しません。つまりそれぞれの質点は自分のペース(自然振動数)で回り続けるだけであり、まだ同期現象は発生しません。では、次のステップに進みます。

ステップ3では質点の運動を定める微分方程式に上図の項を加えます。の運動を決める微分方程式にからが登場することで、初めて変数間の相互作用が発生します。これで蔵本モデルの完成です。

この相互作用項の主要な部分はになります。

の微分方程式の右辺の相互作用項を考察していることに注意して、がより少しだけ大きい場合*1、は正になりますので、はから回るスピードが速くなるように相互作用を受けます。

逆にがより少しだけ小さい場合は、はから回るスピードが小さくなるように相互作用を受けます。

という相互作用によりさんとさんがお互いにお近づきになりたい気持ちがあるということがわかっていただけると思います。実際はから全てから相互作用を受けるので、だけの相互作用を考えるだけでは、回るスピードが速くなるのか遅くなるのかはわかりません。

はで和を取っています。質点の個数が大きくなっても相互作用項が大きくなり過ぎないように相互作用項の分母にが入っています。

また、は相互作用項の大きさを決めるパラメータになります。このが大きければ大きいほど同期現象が起こりやすくなります。つまりは、(次スライドに続く)

つまりは、空気(Kuki)を読む力です。

図のようにさんに比べて少しだけ遅れているさんはさんにおいて行かれないように頑張って速く回ろうとします。逆にさんはさんが遅れていることに気づいて、ペースを落としてあげようとします。

このように空気を読んで相手を思いやる力の大きさ、それがなのです。

を大きくするに従って、同期が発生しやすくなる。これが蔵本予想の要となります。

ここで、同期の発生具合を定量的に把握するための指標を定義しておきます。

個の質点が半径1の円周上を運動している時に、個の質点の重心*2と円の中心との距離を同期具合と呼ぶことにします*3。

図では青い点が質点の重心となっています。全く同期が発生していない場合の同期具合はですが、同期現象が現れると同期具合はだんだんに近づいていきます。

数式ばかり見ていてもイメージが湧かないので、空気を読む力を大きくしていくと、同期具合も大きくなっていくことを実際にシミュレーションをして確認したいと思います。そのためのモデルとしては、(次スライドに続く)

シミュレーションのモデルとしてはクマさんの着ぐるみのバイトの子を使いましょう*4。図のバイトの子はクマさんの被り物を一定のペースで付けたり外したりする趣味を持っています。そんなバイトの子を30人集めて、各々自分のペースで趣味を楽しんでもらいましょう。ただいつもと違うのは周りに同じ趣味を持つ子が29人いることです。空気を読む力を大きくしていくと、どうなるでしょうか?

【空気を読む力】
みんな自分のペースで楽しんでいます。

【空気を読む力】
変わりはないように見えます。

【空気を読む力】
みんなのペース、タイミングが同じになってきています。

【空気を読む力】
何かのお遊戯会のように足並みが揃っています。

確かにを大きくしていくと同期具合が大きくなっていっていることがわかりますね。では最後に蔵本予想とは何かをざっくり説明します。

蔵本予想
の極限で、空気を読む力と同期具合の関係は図のグラフのようになる。

ポイント1:
空気を読む力が小さい間は同期具合は0のまま。空気を読む力がある値(←自然振動数の確率密度関数だけに依る値)を超えると、同期具合が大きくなり始める。

ポイント2:
空気を読む力がに近い時、同期具合はに比例する。

ポイント1のように状態の変化具合がを境に急に変わること(微分が不連続になること)を相転移といいます。固体が液体に、液体が気体になる現象と同じ定義です。みんなが多少空気を読んだところで全く同期が起きません。空気を読む力を上げていくと、急に同期が起こり始め「え？さっきまでみんな同期してなかったのに急にどうしたんだよ？」という状態になります。これが蔵本予想なのです。(先ほどのシミュレーションではでは同期が起きてなさそうでしたが、では明らかに同期が発生していました。)

今回の記事はインターネットに公開されている千葉逸人准教授の下記論説の最初の2ページくらいを日曜数学会発表用に自分なりに解釈してまとめたものです。

http://www2.math.kyushu-u.ac.jp/~chiba/paper/sugaku2016.pdf

私の理解が至らず説明不足の点*5もありますし、解釈、説明が間違っている箇所もあるかもしれません。今後、何かの文献で証明を体得できたあかつきには、正しいステートメントで記事を書きたいです。まずは、「同期現象に関する蔵本予想というものがあって、それは空気を読む力と同期具合に関するものなんだ。そして、千葉逸人准教授が証明されたんだ。」ということを知っていただければ幸いです。

おまけ

今回行ったバイトの子のシミュレーションをするためのソースコードは下記になります。
ソースコードと言ってもただのhtml(javascriptも含みますが)なので、Internet ExplorerやSafariなどのブラウザがあれば自分のパソコンに閉じた世界で遊べます。(Safariでしか動作確認していません。ご了承ください。)

ソースの内容をkumamoto.html等の"html"拡張子でローカルに保存し、ダブルクリックで実行することで動かせます。(ただし、バイトの子と、クマさんの画像ファイルに代わる画像ファイルを何か2つ用意し、htmlファイルと同階層においてください。その後、ソース内の画像ファイル名を指定する箇所をそのファイル名で置換してください。)

<html lang="ja">
  <head>
    <meta charset="utf-8" />
    <title>Kuramoto Simulator</title>

    <!-- javascriptで実装する。 -->
    <script type="text/javascript">
      const NUM = 30; // 質点の数(変更してもいいが、バイトの子の描画は対応できていない。)
      const WIDTH = 400;  // 描画領域の横幅
      const HEIGHT = 400;  // 描画領域の縦幅
      var omega = new Array(NUM); // 自然振動数
      var theta = new Array(NUM); // 変数θ
      var theta_next = new Array(NUM);  // 次の時刻でのθを計算するための一時変数
      var r =  new Array(NUM);  // 質点の色を保持する変数 red
      var g =  new Array(NUM);  // 質点の色を保持する変数 green
      var b =  new Array(NUM);  // 質点の色を保持する変数 blue
      var ctx_circle;  // Canvasの2Dコンテキスト(使い方しかわかっていない)
      var ctx_kuma;

      var RAD = 150;  // 円周の半径
      var delta_t = 0.01; // 計算するときの1ステップの時間幅
      var K = 0.0;  // 空気を読む力 K

      var timer;  // startボタン、stopボタンで制御するためのタイマー変数(使い方しかわかっていない)

      var img_woman = new Image(); // バイトの子の画像
      var img_kuma = new Image(); // クマさんの画像


      // startボタンを押した時の処理
      // 一度止めて、Kの値を更新して再び動かす。
      function start(){
        clearInterval(timer);
        K = document.getElementById('K_VALUE').value;
        // 33msec間隔でdraw(描画)メソッドを呼び出す
        timer = setInterval(draw, 33);
      }

      // stopボタンを押した時の処理
      function stop(){
        clearInterval(timer);
      }

      // ネットで見つけた正規分布に従う乱数を発生させる関数
      /**
        * 正規分布乱数関数 参考:http://d.hatena.ne.jp/iroiro123/20111210/1323515616
        * @param number m 平均μ
        * @param number s 分散σ^2
        * @return number ランダムに生成された値
       */
      function seiki(m, s) {
        var a = 1 - Math.random();
        var b = 1 - Math.random();
        var c = Math.sqrt(-2 * Math.log(a));
        if(0.5 - Math.random() > 0) {
          return c * Math.sin(Math.PI * 2 * b) * s + m;
        }else{
          return c * Math.cos(Math.PI * 2 * b) * s + m;
        }
      }

      // 初期処理 htmlが読み込まれたタイミングで処理が走る
      function init(){
        // Canvasの2Dコンテキストの取得
        ctx_circle = document.getElementById('circle').getContext('2d');
        ctx_kuma = document.getElementById('kuma').getContext('2d');

        // 各質点の色、自然振動数、初期値の設定
        for(var i = 0; i < NUM; i++){
          
          // r,g,bいずれも乱数にすると見た目が良くないので、rは255に固定する。
          r[i] = 255;//Math.floor(Math.random() * 256);
          g[i] = Math.floor(Math.random() * 256);
          b[i] = Math.floor(Math.random() * 256);

          // 自然振動数は平均1、分散1になるように設定
          omega[i] = seiki(1.0,1.0);
          
          theta[i] = Math.random()*2*Math.PI;
        }

        // 画像ファイルの設定
        img_woman.src = "pose_kiri_woman.png"; // TODO なんでもいいので画像ファイルに差し替えてください
        img_kuma.src = "kuma.gif"; // TODO なんでもいいので自分が持っている画像ファイルに差し替えてください

        // 描画をスタートする。
        start();
      }

    // 描画メソッド(この中で微分方程式の差分の計算もしている。。。メイン部分) 
    function draw(){

      // 微分方程式の計算
      keisan();
      // 円周上の運動の描画
      draw_circle();
      // バイトの子の描画
      draw_kuma();
    }

    // 微分方程式の計算
    function keisan(){
      // 10ステップを計算する。1ステップごと描画していた遅々とアニメが進まなかったため。
      for(var l=0;l<10;l++){
        // 微分方程式の差分の計算部分
        for(var i = 0; i < NUM; i++){
          // 相互作用のsin部を足すための一時変数
          var sum_sin = 0.0;
          for(var j=0;j<NUM;j++){
            sum_sin += Math.sin(theta[j]-theta[i]);
          }
          theta_next[i] = theta[i] + (omega[i]+K*sum_sin/NUM)*delta_t;
        }
        // 次のθの値で現状のθを更新
        for(var i = 0; i < NUM; i++){
          theta[i] = theta_next[i];
        }
      }
    }

    // 円周上の運動の描画
    function draw_circle(){
      // 画面描画の更新仕様に関するおまじない
      ctx_circle.globalCompositeOperation = "source-over";
      ctx_circle.fillStyle = '#FFFFFF';
      ctx_circle.fillRect(0, 0, WIDTH, HEIGHT);

      // 円周の描画
      ctx_circle.beginPath();
      ctx_circle.fillStyle = '#000000';
      ctx_circle.arc(convertX(0), convertY(0), RAD, 0, Math.PI*2.0, true);
      ctx_circle.stroke();
 
      // 円周上の質点の描画部分
      for(var i = 0; i < NUM; i++){     
        //更新した座標で円を描く
        ctx_circle.beginPath();
        ctx_circle.fillStyle = 'rgb(' + r[i] + ',' + g[i] + ',' + b[i] + ')';
        ctx_circle.arc(convertX(Math.floor(RAD*Math.cos(theta[i]))), convertY(Math.floor(RAD*Math.sin(theta[i]))), 10, 0, Math.PI*2.0, true);
        ctx_circle.fill();
      }

      // 重心の描画部分 まず平均を出して、描画する。
      var heikinX = 0.0;
      var heikinY = 0.0;
      for(var i = 0; i < NUM; i++){
        heikinX += RAD*Math.cos(theta[i]);
        heikinY += RAD*Math.sin(theta[i]);
      }
      heikinX/=NUM;
      heikinY/=NUM;
      ctx_circle.beginPath();
      ctx_circle.fillStyle = '#0000FF'; // 色は青固定
      ctx_circle.arc(convertX(Math.floor(heikinX)), convertY(Math.floor(heikinY)), 10, 0, Math.PI*2.0, true);
      ctx_circle.fill();
    }

    // バイトの子の描画
    function draw_kuma(){

      // 画面描画の更新仕様に関するおまじない
      ctx_kuma.globalCompositeOperation = "source-over";
      ctx_kuma.fillStyle = '#FFFFFF';
      ctx_kuma.fillRect(0, 0, WIDTH, HEIGHT);

      for(var i=0;i<6;i++){
        for(var j=0;j<5;j++){
          ctx_kuma.drawImage(img_woman, convertX(-175+60*i), convertY(150-70*j),40,40);
          ctx_kuma.drawImage(img_kuma, convertX(-185+60*i), convertY(170-70*j+15*Math.sin(theta[i+6*j])),50,40);
        }
      }
    }

      // htmlの座標の考え方が画面左上を原点、画面右に向かってx軸、下に向かってy軸になっており、わかりにくい。
      // 画面描画の中心を原点、画面右にx軸、画面上にy軸を取る数学で通常使う座標系から
      // htmlの座標系へ変換する関数
      function convertX(x){
        return x+WIDTH/2;
      }
      function convertY(y){
        return -y+HEIGHT/2;
      }

    </script>

    <style type="text/css">
      canvas { background-color:#FFF; border: 1px solid #999; }
    </style>
  </head>

  <!-- 画面表示部分 -->
  <body onload="init();">
    <!-- 各種ボタン、Kの値を設定するテキストボックス -->
    <input type="button" value ="start" onclick="start()">
    <input type="button" value ="stop" onclick="stop()">
    <input type="button" value ="reset" onclick="init()">
    K=<input type="text" id="K_VALUE" value ="0">

    <!-- javascriptのCanvasという仕様で描画する。
        円周上の運動と、バイトの子の運動の2つ描画領域を作成する。
        ブラウザのウィンドウの大きさによらず横に並べたいのでtable内に作成する。-->
  　<table>
      <tr>
        <td>
          <!-- 制御を行うため"circle"というidを付けたCanvas部品 -->
          <canvas id="circle" width="400" height="400">
          </canvas>
        </td>
        <td>
          <!-- 制御を行うため"kuma"というidを付けたCanvas部品 -->
          <canvas id="kuma" width="400" height="400">
          </canvas>
        </td>
      </tr>
    </table>
</html>

なお、作成にあたって下記サイトを参考にしました。
http://yoppa.org/taumedia10/2065.html

いろいろいじって遊んでみてください。

*1:実際には2の整数倍の違いを無視して考えているので、「絵的に少しだけ前にいる場合」という表現の方が良い気がします。

*2:個の質点の質量は等しいものとします。

*3:同期具合という言葉はこの記事で勝手に作った言葉です。

*4:日曜数学会ではポケモンのナッシーをモデルにしましたが、ブログでナッシーを使うと面倒なことになりそうなので、フリー素材を使います。

*5:自然振動数の確率分布に関すること。漸近安定の概念。そもそもシミュレーションのは有限であったが、蔵本予想は。

素数大富豪〜素数大富豪数判定機を作ってみた〜

この記事は、素数大富豪 Advent Calendar 2016 - Adventar 24日目の記事です。23日目はicqk3さんの素数大富豪ver2です。

icqk3さんの素数大富豪 ver.2にて「ラマヌジャン革命」が追加実装されていますが、「ラマヌジャン革命」と共に新たに公式ルールに加わることが決まった「合成数出しにおける指数表記出し」も実装されているようです。仕事が早い!

はじめに

今素数大富豪が数学好きの間で静かなブームになっています。「素数大富豪って何ですか?」という方は、本アドベントカレンダー1日目のにせいさんの記事を読んでください。

nisei.hatenablog.com

私は素数大富豪を1回しかやったことがなく、戦略やゲームの中で出会った素数達について語れるレベルではありません。その観点では本アドベントカレンダーで素数大富豪の玄人の方たちが存分に語っていますので、ぜひ読んでください。

私はコンピュータを使って面白いことわからないかなぁという観点で素数大富豪 AdventCalendar 2016に2回分登録させていただきました。本記事はその2つ目の投稿で、1つ目は12月6日に投稿しています。こちらも読んでいただけたら幸いです。

mattyuu.hatenadiary.com

素数大富豪数とは

素数の観点から考えると、1より大きい任意の整数は素数か合成数かのいずれかになります。そして素数大富豪の観点から考えると、1より大きい任意の整数は素数大富豪数か非素数大富豪数のいずれかになります。

この記事では素数大富豪数を下記で定義しています。

素数大富豪数
素数大富豪にて、ペナルティを受けることなく手として出しうる数を「素数大富豪数」と呼ぶ。また、1より大きい整数のうち「素数大富豪数」でない数を「非素数大富豪数」と呼ぶ。

まず、素数大富豪素数*1はいずれも素数大富豪数になります。最大素数大富豪素数より大きい素数は、素数大富豪にて手として出すことができないため、全て非素数大富豪数になります。

素数大富豪には「合成数出し」というルールがあるため、素数大富豪数は合成数も含まれることに注意が必要です。例えば公式ルールで解説されているという合成数はとなるため、、、、、のカードを捨てることで場に出すことができます。そのためは素数大富豪数になります。

しかし、はですが、ジョーカー2枚をとして使っても7枚のを場に捨てることができません。そのためは非素数大富豪数になります(実は最小の非素数大富豪数です。)。

なお、本アドベントカレンダー22日目のせきゅーんさんの下記の記事にて、次回のルール改版時に「合成数出しにおける指数表記出し」ルールが公式ルールとして追加されることが予告されました。

integers.hatenablog.com

せきゅーんさんの記事でも言及されていますが、指数表記出しを行うことでは素数大富豪で出せるようになり、晴れて素数大富豪数に昇格する見通しです。なお、指数表記出しルール追加後の最小の非素数大富豪数はになります。突然の指名でもさぞかし驚いていることでしょう。今度はどうかも救ってあげてください。

素数大富豪数判定機

1より大きい整数を素数の観点、素数大富豪数の観点で分類すると、下記の4分類になります。1より大きい任意の整数は下記の分類のどこかただ1つだけに所属しています。

• 素数大富豪素数 (素数大富豪数 かつ 素数)
• 素数大富豪合成数 (素数大富豪数 かつ 合成数)
• 非素数大富豪数の素数 (非素数大富豪数 かつ 素数)
• 非素数大富豪数の合成数 (非素数大富豪数 かつ 合成数)

素数であるか否かは、(簡単かどうかは別にして)素因数分解を行うことで判定できます。しかし、素数大富豪数かどうかの判定は簡単でしょうか。

例えば、

という数を見てこれが素数大富豪数かどうかを判定するのは難しいと思います。

数字列の最後のの箇所でのカードとのカードを出すべきか、のカードを出すべきかパッとわかりません。素因数にが出てくるのであればのカードは温存しておくべきでを出す必要がありそうです。しかし、素因数にが出てくるのであれば逆にを温存しておかないとカードが足りなくなります。

今回、1より大きい整数を入力すると、

• その数が4つの分類のうちのどの分類になるのか
• 素数大富豪数の場合に、どのようにカードを出せばいいのか

を出力する素数大富豪数判定プログラムを作成しました*2。

本当はどのようなアルゴリズムで素数大富豪数を判定しているのかを紹介したかったのですが、「合成数出しにおける指数表記出し」ルール追加後のプログラム修正時等の別の機会にさせていただきます。今回新ルールでの判定ロジックも作りたかったのですが、12月22日に追加されたルールということで時間が足りませんでした。新ルールでは分割数とか考える必要がありちょっと難しそうです。

この素数大富豪数判定機があれば、身の回りに溢れるあらゆる数たちが素数大富豪で活躍できる数であるかどうかがわかります。今回は素数大富豪数判定機を使って、いろいろな数の判定をしましたので、その紹介を行い締めさせていただきます。以下乱文が続きます。。

明日は本アドベントカレンダーの作成者にせいさんによるまとめの記事です。ありがとうございました。

最大素数大富豪メルセンヌ素数

の形をした素数をメルセンヌ素数といいます。8番目のメルセンヌ素数()までは素数大富豪素数であることがわかりました。そして9番目以降のメルセンヌ素数は非素数大富豪素数でした。そもそもメルセンヌ素数はに対して爆発的に大きくなっていくので、すぐに最大素数大富豪素数より大きくなってしまいます。

最大の素数大富豪数かつメルセンヌ数(最大素数大富豪メルセンヌ素数)は、8番目のメルセンヌ素数である

で、最小の非素数大富豪数のメルセンヌ素数は(最小のエデンの園メルセンヌ素数)、は9番目のメルセンヌ素数である



でした。なお、エデンの園素数とは素数大富豪で出すことができない素数です。

integers.hatenablog.com

最小のエデンの園双子素数

双子素数というのは差がである素数の組のことです(せきゅーんさんによると、「数の組は素数とは言えないため、素数双子と呼ぶべき」とのことです。)。

最小の非素数大富豪数の双子素数(最小のエデンの園双子素数)は


と

でした。

最小のエデンの園非正則素数

非正則素数とはなんですか?という方は下記をご参照ください。

integers.hatenablog.com

最小の非素数大富豪数の非正則素数(最小のエデンの園非正則素数)は



でした。

フィボナッチ数列の素数大富豪数性

フィボナッチ数列は、、、、、、というふうに直前の2項の和を次の項とする数列になります。

最小の非素数大富豪フィボナッチ数(場に出すことができないフィボナッチ数)は

でした。

タクシー数

2番目のタクシー数までは素数大富豪数でしたが、それ以降は非素数大富豪数の合成数でした。

素数大富豪タクシー数

(は合成数出ししなくても「ラマヌジャン革命」の数として使用可能です。)

非素数大富豪数かつタクシー数

タクシー数とはなんですか?という方は下記をご参照ください。

integers.hatenablog.com

ちなみにせきゅーんさんのタクシー数は素数大富豪数の合成数でした。素数大富豪で使用可能です。さすがですね。

integers.hatenablog.com

最大素数大富豪フェルマー数

フェルマー数はの形をした整数です。素数とは限りません。

5番目のフェルマー数までは素数大富豪素数でした。



そして6番目のフェルマー数は素数大富豪数


しかし、7番目のフェルマー数は非素数大富豪数の合成数になります。

それ以降のフェルマー数で素数大富豪素数になるものはありません。よって最大の素数大富豪フェルマー数は、



で、最小非素数大富豪フェルマー数(最小の、非素数大富豪数かつフェルマー数)は、



になります。

最小の非素数大富豪数かつ完全数

でした。

完全数って何?という方は下記をご参照ください。

integers.hatenablog.com

山の高さ

世界的に有名な山の標高はいずれも素数大富豪数の合成数でした。意外に実戦で使えそう?

エベレスト(8,848m)

K2(8,611m)

キリマンジャロ(5,895m)

モンブラン(4,809m)

富士山標高(3,776m)

【その他】
下記のような特徴的な合成数は非素数大富豪数でした。

私の誕生日も非素数大富豪数でした。。。やはりがネック。

*1:「素数大富豪」に手として出しうる素数を「素数大富豪素数」と呼ぶ。by tsujimotterさん

*2:いつかjavascript等で誰もが使えるように公開できれば良いのですが、javascriptだけでは巨大な整数の素数判定が難しい気がします

マーライオン再び〜ラグランジュの未定乗数法を用いて〜

この記事は、日曜数学 Advent Calendar 2016 - Adventar 19日目の記事です。18日目はふにゅさんのガロアがイケメンな件―数学とイメージの関係 - funyuのブログです。

ガロア、いいですね。私は男なのでガロアに恋心を抱くことはありませんが、ガロア理論の基本定理には恋心を抱いてしまいそうです。これまで数論を勉強してこなかったので、ガロア理論が大いに使われていそうな数論を勉強するのが今の楽しみです。

はじめに

以前下記の記事でマーライオンが一番遠くまで水を飛ばすことのできる口の角度を求めました。

mattyuu.hatenadiary.com

前回は空気抵抗を無視しましたが、今回は空気抵抗も考慮して問題を解きます。空気抵抗が入るだけで、問題がぐっと難しくなり、前回と同様の方法では解けませんでした。しかし、ラグランジュの未定乗数法という手法を用いることで、最適解の満たすべき方程式を得ることができましたので、問題を解きながらラグランジュの未定乗数法の強力さを紹介したいと思います。

この記事では前回必要だった高校物理の力学の知識、高校の数Ⅲで習う三角関数の微分の知識に加えて、微分方程式の基礎(変数分離法のみ)、偏微分、指数関数、対数関数の微積分の知識も前提としてしまいます(大学初年度レベルです。)。逆に言うと、数学の知識が増えると解ける問題の範囲も広がるということなので、数学を勉強するモチベーションにもなりますね。

前提知識がない方は、前回同様フジテレビのガリレオで福山雅治さんはこんな数式を書いていたんじゃないか？と想像しながら、数式を流し読みしていただけたら面白いのではないかと思います。

問題設定

では、問題設定から行いましょう。

前回と同様に、水は大きさのない質点として計算していきます。水は常に連続的に噴射され続けていますが、時刻で質量の水分子が1粒発射されたものとして読んでください。また空気抵抗は速さに比例する大きさの力が、運動の方向と逆向きに働くものとします。

では前回と同じ方法で解けるところまで解いていきましょう。口から飛び出る水の速度を水平方向(x軸右方向)の速度と、垂直方向(y軸上方向)の速度に分けて、ニュートンの運動方程式を立てます。

ここで、記載の簡略化のため、と置いています。出発点となる運動方程式から、が消えたため、今後、は用いず、のみを用いることになります。が大きいほど、空気抵抗の影響が大きくなります。

、の導出

との微分方程式をそれぞれ変数分離法で解き、、を導出します。

まずは、です。

次に、を求めます。

無事、、が求まりました。

、の導出

次に、、をそれぞれで積分して、時刻での水の位置を求めましょう。

まずは、から。

次に、です。

前回よりはるかに複雑ですが、、も求まりました。

空気抵抗がない場合は、この、を連立させを消去することで、との関係をという二次関数(=放物線)の形で表すことができましたが、式の形を見ればわかる通り空気抵抗がある場合では二次関数で表すことができません。マーライオンの口から発射された水は、空気抵抗が入ることで放物線とは異なる軌道を描くことなります。

せっかく、が求まりましたので、ここで一休みしてその軌道を見てみましょう。空気抵抗を大きくする程その軌道は歪曲され、遠くまで飛ばなくなることがわかりますね。

地面に落ちる時間が求められない

前回はを解いて、水が地面に落ちる時刻を求め、そこから水平到達距離をの関数で表し、それを微分することで最適解を求めました。しかし、今回は最初の関門であるが解ける気がしません。の中にはの一次関数と指数関数が共に現れています。例えば私は、次のようなシンプルな方程式も解析的に解くことができません。*1

そして、解析的に解くことを諦めて、をコンピュータを使って数値的に解いたとしても、数値解は離散的にしか求められないため、その先の水平到達距離をで微分をするところで行き詰まるでしょう。

私はここでこの問題を解くことを諦めかけました。

しかし、諦めきれず式をいじくり回しているときに、だんだんと頭の片隅から蘇ってくるものがありました。それがラグランジュの未定乗数法だったんです。

ラグランジュの未定乗数法

ここでは、一瞬マーライオンを忘れて、ラグランジュの未定乗数法の紹介をします。(変数の記号は今回の問題に合わせてとで記載しています。)

ラグランジュの未定乗数法
という条件の下、を最大化したいとき、

とおくと、下記の連立方程式の解が、その最適解の候補を与える。

2変数の問題なのに、わざわざ変数を付け加えて3変数にしているのがミソです。大学初年度で習う陰関数定理を用いれば証明が出来ますが、ここでは証明は行いません*2。

さて、このラグランジュの未定乗数法がなぜ今回の問題に関係あるのでしょうか。

先ほど、と、あたかもだけの関数のように、を書き下しましたが、この問題では一番遠くまで飛ばすを求めるという意味で、も変数と考えた方が都合がよく、、と書いた方がより適切です(、、、も値を変更することができますが、ここでは定数という位置付けです。パラメータと呼んだ方がいいかもしれません。)。

先ほど解くことを諦めたという方程式に注目しましょう。これはある角度で発射された水が地面に落ちる時刻を求める方程式と考えてきましたが、逆に時刻で地面に落ちるように口の角度を求める方程式と考えることもできます。その意味でとは全く対等です。

を満たすは、口の角度がのとき、時刻で地面に水が地面に落ちているということを意味します。このようなの組の中でを最大にするものを求めると、そのが求めたい最適の角度になります。つまり、という条件の下、を最大化したいのです。これはラグランジュの未定乗数法の前提そのものですね。

簡単な例

今回の問題をラグランジュの未定乗数法で解く前に、とても簡単な例題を解くことで前回の空気抵抗なしの場合の解法と、この後に行う今回の解法の比較をしてみましょう。

問題
という条件の下、を最大化しましょう。

ではまず、前回の解法から。

直接的な解法
よりとなる。これをに代入して、

となるから、、のとき、最大値をとる。

この解法はの条件からのようにをで表して、という風にをだけの関数で表すことで、通常の1変数関数の最大値問題に帰着させています。この解法の肝はとをの関数で表せたことになります。しかし空気抵抗がある場合のマーライオンの問題のようにそれはいつも可能とは限りません。

では、ラグランジュの未定乗数法を用いた解法を見てみましょう。

ラグランジュの未定乗数法による解法
とする。

ラグランジュの未定乗数法より、最適解を得るには下記の連立方程式を解けばよい。

第1式より、これを第2式に代入して、そして第3式よりを得る。
最大値はとなる*3。

先の解法とは全く違うのに、これで同じ解が得られることに驚きます。

ラグランジュの未定乗数法を用いて解く

さて、いよいよ本来の問題を解くときがきました。まず、条件のを次で定義します。

としてもよいのですが、定数をかけることで記載が簡易になるようにしています。

最大化するもにをかけて、次式で、

また、関数を、次式で、

それぞれ定義します。

関数の準備が整いました。ラグランジュの未定乗数法を用いると、解くべき連立方程式は下記になります。

それでは、解いていきましょう。まずはに注意して、第2式より、

を得ます。いきなりがわかりました。幸先のよいスタートです。

次に、得られたを第1式に代入して、

となり、この両辺にをかけて整理すると、

形は複雑ですが、をの式で求めることができました。では、最後にこれを第3式に代入して整理しましょう。

あとは、これをについて解くだけなのですが、見るからに無理そうです。この方程式を満たすの範囲の解が、求めたい最適解になります*4。

最後の最後で数値解になってしまうことは口惜しいですが、仕方ありません。

最後の式の左辺をではなく、一般の変数の関数とみなして、demosでのグラフを描いてみましょう。

、、、のパラメータをいじることで、関数のグラフは形を変えますが、確かにの範囲に1つだけ解がありそうです。

そして、 を大きくしていくと、最適解は小さくなっていきます。これはの場合によく知られている事実と合致します。

demosで確かめる

残念ながらdesmosには方程式をsolveする機能はありませんので、パラメータを連続的に動かした時の最適解をdesmos上だけで変動させて表示させることはできません。パラメータを固定してを数値計算で求め、desmosを使って実際に最適解が得られていそうということを確認します。前回同様、マーライオンにいろいろな角度で水を発射してもらい、飛距離が最大になる最適解の角度の方向にはオレンジ色の点線を引き、最大到達地点には赤い旗を置いておきましょう。そして、比較のため空気抵抗がない場合の軌道を紫色の点線で表示します。

下記の例では、 、、、としました。その時のはおよそとなります。

うまくいってますね!

まとめ

最後の最後は数値解になってしまいましたが、ラグランジュの未定乗数法を用いて曲がりなりにも最適解を求めることができました。最後に得られた式を使って、空気抵抗がある場合は最適な角度は常に下方に修正されるのか、といったことを調べたら面白いと思うのですが、今回はこの辺りにしておきます。

空気抵抗なし版の問題もラグランジュの未定乗数法を用いて、前回と同じ解析解を得ることができます。やってみるとラグランジュの未定乗数法を用いる方が遥かに簡単でした。一度計算してみたら面白いと思います。

ラグランジュの未定乗数法は大学で習っており、「あぁ、そんなものもあるんだなぁ、便利そうだなぁ」くらいの印象でした。しかし自分が問題設定してラグランジュの未定乗数法を使わないと解けない問題に出会うとその凄さに驚嘆せずにはおれません。「あぁ、楽しい計算だったなぁ」

*1:ここで、解析的に解くとは、「誰もが知っている関数で解を書き下す」という意味で使っています。

*2:https://www.amazon.co.jp/これならわかる工学部で学ぶ数学-千葉-逸人/dp/490381419X参照

*3:ラグランジュの未定乗数法は最大値の候補(極値)を与えるだけなので、最大値となっていることは別途議論が必要です。

*4:実際は極値になるだけですので、最大値になるかの議論は必要です。

麻雀×プログラミング×数学

この記事は、伝道師になろう！ Advent Calendar 2016 - Adventar 11日目の記事です。10日目は狡猾な狐さんの「ARとしての知識を実装して出かけよう！」(予定)です。

はじめに

東京では今年から「伝道師になろう」というイベントが定期的に開催されています。伝道師になろうってなんだろう?」という方は、狐さんの下記の記事を参照してください。

wreck1214.hatenablog.com

簡単に言えば「自分の好きなことを、知らない人にもわかりやすく、なぜ好きかを伝えて、面白さを伝道しよう」という企画です。僕も参加したことがあります*1。

コンセプトが本当に素晴らしいので、来年はこのイベントが全国に広がればいいですね。狐さんによると、ビブリオバトルのように誰が始めたかわからないくらいとのことです。

数学以外に好きなもの

僕が好きなものは絶対的に数学です。伝道できる(と自分で思っている)ものは数学しかありません。しかし、伝道師になろうは日曜数学会から派生したイベントということもあって、このアドベントカレンダーに数学ネタだけを書くのは少し気が引けます*2。

僕は数学以外で好きなものを聞かれると「麻雀」、「プログラミング」、「京都」、「熊野寮」、「料理(←最近やっていない)」、「小籠包」、「ヒカルの碁」から選出して答えていますが、数学とこれらには、好きレベルでいうと、

数学>>>>>>|超えられない壁|>>>>>>麻雀、プログラミング、京都、熊野寮、料理、小籠包、ヒカルの碁(順不同)

くらいの差があります。数学に関しては永遠に熱く語る自信がありますが、その他の好きなものは最高でも3時間程度しか語れない気がします。ただその他の好きなものも数学とコラボさせることでそれなりのボリューム、ネタになるのではないかと思い、今回「麻雀」、「プログラミング」を選抜して、投稿しました。

まず最初に、伝道師になろうのルールに則って、「麻雀」、「プログラミング」、「数学」がそれぞれなぜ好きなのかを語っていくことにしましょう。

麻雀が好きな理由 (半分は熊野寮の話)

麻雀が好きな理由を2点挙げます。

まず1点目は運の流れを感じることができる、そして運がいい時は最高に気持ちがいいということです。

普段生活の中で運がいいとか、悪いとかを考えることは少なくなってきましたが、麻雀をやっていると何をやってもうまくいく無双状態というものを体感できます。とにかく配牌(最初に配られる牌)がいい、とにかくいい牌をツモる(牌を引くこと)、そしてとにかく点数が高い状態です。まさに下記の女子プロの豊後さんのような状況です。

【麻雀】 ブンゴ無双 【役満】

無双状態は滅多に発生するものではありませんが(感覚的には5半荘に一回)、無双状態になった時の快感を味わうために麻雀をやっていると言っても過言ではない気がするくらい楽しく気持ちいいです。

2点目は仲間と語り合いながらやるとやっぱり楽しい、というところです。

(ここからは熊野寮の話を交えつつ説明していきます。)

僕が麻雀を覚えたのは大学生時代の時です。先に挙げた数学以外の好きなものの中に「熊野寮」というものがありましたが、僕は学生時代に熊野寮に6年間住んでいて、そこで先輩に麻雀を教わりました。熊野寮は古いですが最高の寮です。素数大富豪の大会が開催された最初の場所でもあり、最近のトレンドをいち早く吸収するあたりはさすがと思います。Googleで"熊野寮"を画像検索するとその凄さをわかっていただけると思いますので、是非調べてみてください。なお、家賃は700円です。ただ電気代や食堂のお姉さんたちの保険料等が追加され、実際は4,100円でした。それでも安い!

熊野寮にはA棟、B棟、C棟があり、それぞれ各階に談話室があります。僕はA棟3FのA3談話室に住んでいました。これは談話室に入り浸っていたという比喩的な表現ではなく、談話室の片隅に本棚で人一人分寝れるスペースを作って、そこに住んでいました。談話室には大学生の娯楽が詰まっています。ゲーム、漫画、お酒、麻雀。。。みんな好きな時に談話室に来て、好きなことをして語り合っていました。今思っても楽しい空間です。そして下記理由から麻雀こそ仲間との語り合いにピッタリな遊び、ゲームだと思うのです。

• 手を動かすだけで疲れないから長時間できる
• ご飯食べながらでもできるから長時間できる
• 時々「ポン、チー、ロン、ツモ」という以外は発声の必要がないいからお話しができる

実際、談話室でやる麻雀は娯楽でやる麻雀ですので、いつも楽しく語り合っていました。朝まで仲間*3と語りながら麻雀をやることも珍しくなかった僕としては、麻雀は語り合いのゲームで楽しいんだ!ということを伝道したいと思います*4。

女子用の雀荘(タバコは絶対禁止、フードメニューにスイーツ、カクテル多め)とか作れば、女子会にピッタリな気がしますね。

では麻雀が好きな理由はこれくらいにして、先に進みましょう。

プログラミングが好きな理由

これに関しては、数学の計算ができるからという一言に尽きます。コンピュータというのは和訳すると「計算機」ですし、プログラミングはコンピュータに命令を与えるものですので、「計算機に命令を与えるもの」がなぜ好きかと聞かれて、「計算ができるから」と答えてるだけになります。何の回答にもなっていないように思えますが、その言葉以上に計算できることは素晴らしいと思うのです。

例えば、あなたがお望みであれば僕は4,294,967,297や147,573,952,589,676,412,927が素数でないことをプログラミングで簡単に示すことができますが、一昔前はそれは大変難しいものでした。

4,294,967,297に関してはtsujimotterさんの下記の記事を、
tsujimotter.hatenablog.com

147,573,952,589,676,412,927に関しては、下記のフランク・ネルソン・コールの逸話をご参照ください。
メルセンヌ数 - Wikipedia

上記の記事にあるように、昔の人は20桁程度の素因数分解ですら難しかったのです*5。円周率の計算に一生を費やした人がいます。そして死後に誤りを指摘されてしまった悲しい人もいます。その人達が一生を費やして計算した円周率の値は、おそらく僕は30分程度プログラミングをすると手に入れることができます。

17世紀のケプラーはブラーエが残した大量の観測データから、地球が楕円軌道で太陽の周りを回っていることを突き止めました。また、18世紀のオイラーががと予想したのも*6、19世紀にガウスが小惑星ケレスを発見できたのも全部大量の計算の賜物でしょう。

僕自身も前回のブログで書いた素数大富豪の会心の一撃のシミュレーションは、プログラミングをしなければ一生かかっても終わらなかったでしょうし(というか絶対途中でやめる)、プログラミングをせずにゼータ関数の零点を計算するのがいかに大変であるかを経験したこともあります。

ネイピアが対数を発見するために引きこもった強い動機となったように、昔の人の計算との戦いは想像を絶するものだったと思います。もしオイラーやガウスにプログラミングを教えてあげれば、二人は泣いて喜ぶのではないでしょうか*7。プログラミングをすることでそのような計算をいとも簡単に行うことができる。直接的な理由ですが、これがプログラミングを好きな理由です。

数学が好きな理由

これは語ると切りがありませんし、語り切れるとも思えません。そしてまだまだ自分でもなぜ好きがかわからない状況です。ちょうど半年くらい前に自分がなぜ数学が好きなのかをマインドマップで殴り書きしていました。狂気じみていますが、こちらを貼り付けることで好きな理由に代えさせていただきます。

ついでに同じタイミングで数学ってどんな分野があるかも殴り書きしていました。

どちらも何も見ずに5分くらいで書き上げたものです。汚い字で読めないですが、それだけ好きなんです、

ただ、これじゃ全然伝道していないので、1点だけ言わせてください。(ここから先はあくまで持論です。)

「数学は紙とペンがあればどこでもできる*8」ということを好きな理由として強調したいです。これは「紙とペンがあれば計算できるしね」みたいな単純な話ではありません。数学的実体なんてこの世のどこにも存在しません。 虚数はその名の通り現実に存在しないような名前が不本意に与えられていますが、実数の1という数はどこに存在していますか？紀元前にピタゴラスによってピタゴラスの定理が発見されましたが、ピタゴラス以前にもピタゴラスの定理は成り立っていたはずです。ピタゴラスの定理はどこにあったのでしょうか?

1もピタゴラスの定理もこの世界のどこにも存在しません。でもこの世界のどこにでも存在しているのです。そして紙とペンを使うことでその数学的実体の化身が目の前に現れ、時代、人種、性別、年齢を超えて他の人とも寸分違わず同じものを認識しあえるのです。それは本当に奇跡のようなことだと思います*9。こんな奇跡を体感できるなんて。。。はぁはぁ。。数学ってすごいですよね。

この話はエドワード・フレンケルさんの「数学の大統一に挑む」から影響を受けていると思います。

数学の大統一に挑む

また、日曜数学者の始祖であるtsujimotterさんも過去にtwitterで「旅行に行っている暇がない。今は数学的世界を探索するのに忙しい。」のようなことをつぶやいておられました。過去のツイートなので探しきれませんでした。まさに同感で、僕らは紙とペンを使うことで、この世界よりもずっと広大な数学的世界を探検できるのです。。。はぁはぁ。。数学ってすごいですよね。

いよいよコラボ まずは麻雀の基本説明

なぜ好きかの説明が終わりました。「麻雀」×「プログラミング」×「数学」のコラボをしたいと思います。

そのためには最低限麻雀のことを知る必要がありますので、説明します。

まずは麻雀牌にどのようなものがあるかを説明します。麻雀牌は大きく数牌と字牌に分かれるのですが、この後の考察に字牌は不要ですので、数牌だけを考えます。数牌には萬子(マンズ)、筒子(ピンズ)、索子(ソーズ)の3種類があり(これを色と言います)、それぞれ1から9の数字が書かれています。色と数字が同じである牌はそれぞれ4枚あります。つまり数牌は3(色)×9(数字)×4=108枚存在します。

次にアガリの形を説明します。麻雀は14枚の牌を「3枚1組のグループ4つ」と「2枚1組の雀頭(ジャントウ)１つ」の形にすることでアガることができます。「3枚1組」は全く同じ牌3枚でもいいですし、同じ種類の牌で2,3,4のように3つの連続する整数の組でも良いです。雀頭は全く同じ牌の2枚組になります。

下記がアガリの形の例になります。

麻雀は基本的には手持ちの牌は13枚になっています。13枚の状態で1枚牌を引いて、14枚の状態になった時に、アガリの形になっていればアガることができます。アガれない場合は1枚引いたので、手持ちの14枚の牌どれでもいいので1枚捨てて再び13枚の状態にします。このようにアガリの形になるまで牌を交換し続けるゲームになります。アガリの形が特定の条件を満たせば役というものが付きます。役が珍しいものであればあるほどアガった時にもらえる点数が多くなります。

最後に、待ち牌について説明します。次に良い牌を引けばアガれる状態のことをテンパイしているといいます。テンパイしている時に引くことでアガれる牌、つまりアガるために待っている牌を待ち牌といいます。下記の例のように待ち牌は1種類とは限りません。

いろんなパターンの待ち牌がありますね。

以上で麻雀の基本説明を終わります。

第二の九蓮宝燈探索

唐突ですが、13枚の手持ちの牌が次の形の時、1〜9の牌全てが待ち牌になります。つまり1〜9のどの数牌を引いてもアガることができます。

実際に確かめてみると、確かにアガリの形になっています。

なお、この形でアガると九蓮宝燈(チューレンポートウ)という役の中でも特別な役満という役になります。九蓮宝燈はアガったら死んでしまうという迷信があるくらい珍しい役になっております。

「1〜9のどの牌がきてもアガれるなんて九蓮宝燈はすごいなあ。」と思うところですが、知られていないだけで、他にも1〜9のどれがきてもアガれる13枚の手牌が存在するも知れません。そんな未だ日の目を見ない第二の九蓮宝燈を見つけてあげたい、見つかったら僕だけでもそいつのことを役満と呼んであげたい。しかし、麻雀の手牌の組み合わせはそれなりに大きい数になりそうだし、それぞれの手牌でちゃんと待ち牌を漏れなく見つけられるか不安。。。。。

そんな悩みを解決するのがプログラミングなんです！

コンピュータはプログラミングした通りに高速に、嫌とも言わず、間違うことなく動いてくれます。正しくプログラミングすれば正しい結果が得られます。今回はどのようにプログラミングしたかの紹介はしませんが*10、実際にプログラミングして実験した結果、九蓮宝燈以外には1〜9の全てが待ち牌になるような手牌は存在しませんでした。

第二の九蓮宝燈が見つからなかったのは悲しいですが、それだけ九蓮宝燈はすごいものなんだ!ということがわかりました!

「プログラミングって強力だなあ。家に麻雀牌なくてもこういうことがわかるんだからなあ。」と思います。

一定の成果を得ましたが、まだ「麻雀」×「プログラミング」止まりです。

数学的に意味がある待ち牌

さて、プログラミングによって色々な手牌の待ち牌を調べられるようになりました。では最後に数学的エッセンスを加えて本記事を締めくくりましょう。

スライドを見ていただければ、説明は不要です。なお、不思議なことに下記の4種類すべてちょうど2パターンずつでした。

最後はみんな大好き素数です!

明日はHaru Negamiさんの「好きすぎて食べちゃいたい◯◯」です(^_^)

ありがとうございました。

*1:今回は学生時代の話をするため、一人称は「僕」を使いたい気分です。

*2:数学に限らず好きなものをどんどん発表していこう!というのが元々の誕生理由な気がするため。

*3:熊野寮のメンバーは家族でも友達でもない仲間という表現がよく当てはまる気がします。

*4:しかし熊野寮のような特殊な環境はほとんどありません。誰かのアパートで麻雀しても多分隣の部屋の人からうるさいと怒られるでしょう。雀荘に行ったらお金がかかります。仲間が集い会えるような場所が欲しいところです。

*5:本質的には今も難しいです。RSA暗号の基本原理です。でもそれはまた別のお話。

*6:オイラーは後にちゃんと証明しています。

*7:しかし、この二人は数学界の偉人中の偉人で常任にはその底は計り知れないので、コンピュータどころでは泣いて喜ばない気もします。オイラーは人が呼吸をするように、鳥が空を飛ぶように計算していたと言われています。

*8:実際は教科書も欲しいところ。

*9:かなりスピリチュアルなことを言っていますが、哲学的な話は大の苦手です

*10:汚いソースを見られるのは超恥ずかしいため。