今回は調和級数と調和級数が大好きなカメさんのお話をしたいと思います。「調和級数って何?」っていう説明もしますので、知らない方も安心してください。
ちりが積もっても山にならない
俗世間では「ちりも積もれば山となる」とよく言われますが、数学の世界にはちりが積もっても山とならないようなものが存在します。
例えば、
という無限個の足し算を考えると、この無限個の足し算は明らかに、
という風に小数点以下にが並ぶ数となり、この結果は2を超えることはありません。足していく数は全て0より大きいため、足し算を続ければ続けるほど足し算の途中結果はどんどん大きくなっていきます。
ちりのように小さい数がどんどん足されて、どんどん大きくなるのにを超えないのです。
今度は、次のような無限個の足し算を考えてみます。分母が、
、
、
、
とどんどん倍になっているものです。
下の図から明らかのように、足し算を続ければ続けるほど途中の結果はに近づいていきます。こちらの無限の足し算の結果も
を超えることはありません。
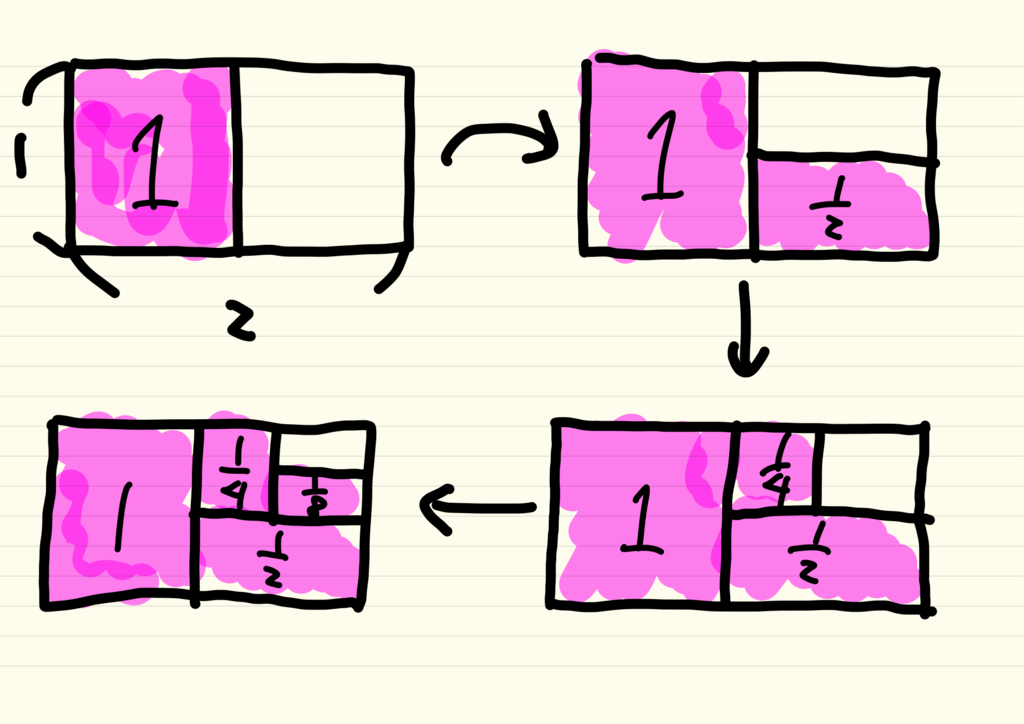
たしかに数学の世界ではちりが積もっても山とならないような例が存在します。
調和級数
ちりが積もっても山にならない例を知った上で、本題の調和級数の話をします。
下記の無限個の足し算を調和級数と言います。
この足し算は現実世界でちりが積もって山になるのと同じように、無限に大きくなるでしょうか?それとも、前述した2つの足し算同様に、ある値(前述の例では2)が存在して、どんなに頑張ってもその値を超えることはないのでしょうか?
調和級数も前述した例と同様に、足し算を続けていくと、「1兆分の1」、「1兆1分の1」、「1兆2分の1」、、、と足す数はどんどん小さくなっていきます。
「1兆分の1」はなので、全体の和はほとんど増えないことがお分かりいただけるかと思います。
しかし調和級数は足し算を続けていくとあらゆる数より大きくなります。例えばあなたが「100兆!」と言ったら、いつか調和級数の和も100兆を超えます。これはなかなか不思議なことです。本当にちりのようなどんどん小さくなる分数たちが、どんどん足されていくことでいつしかどんな数をも超えていくのです。このことを調和級数は発散するといいます。
下表に調和級数の途中までの和()が初めて
〜
を越える時の
をまとめました。
まで足してやっと
を越えるということで、非常にゆっくり、そして着実に大きくなることがわかります。

調和級数が発散することの証明はインテジャーズに書いておりますので、是非読んでみてください。
調和級数大好きカメさん登場
ここで今後の話をイメージしやすくするために調和級数が大好きなカメさんを登場させます。
調和級数は非常にゆっくりですが少しずつ大きくなり、いつしかあらゆる数より大きくなるものでした。カメさんもその歩みは遅いですが、非常に努力家なので、地道に歩き続けどんな遠くにも行ってしまいます。
ここに調和級数と努力家な自分にシンパシーを強く感じるカメさんがいます。いつしか他の動物たちから調和級数大好きカメさんと呼ばれるようになりました。

調和級数大好きカメさんは、調和級数が大好きなので歩く歩幅は調和級数に倣っています。つまり最初の一歩の歩幅は、次の一歩の歩幅は
、その次は
です。調和級数のように数直線上で0を出発地点として、数直線を歩き続けます。
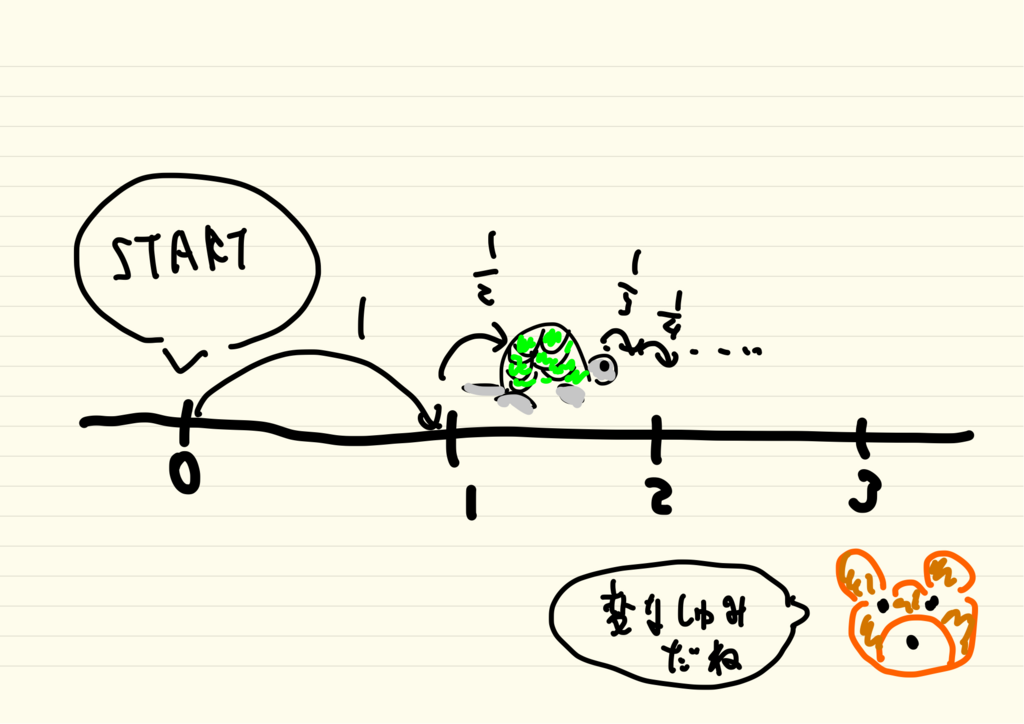
調和級数は発散するため、調和級数大好きカメさんはいつしか1000、いつしか100兆を超えて行きます。

喉が乾く調和級数大好きカメさん
調和級数大好きカメさんがいくら努力家だと言っても生き物です。飲まず食わずでは歩き続けることはできません。

そこで数直線上の整数点に給水所を設けてあげることにしました。給水所では水とバナナが供給されます。

ただし、1つだけルールがあります。調和級数大好きカメさんがぴったり整数の点に止まれた時だけ、つまりぴったり給水所にたどり着いた時だけ、水を飲み、バナナを食べても良いというルールです。
調和級数大好きカメさんのスタート地点はで最初の一歩の歩幅は
ですから、一歩歩いて整数
の地点に止まりますので、調和級数大好きカメさんは水を飲みました。今はそんなにお腹は空いていないということで、「バナナは次の給水所で食べる」と言い残し、出発しました。

しかし、
なので、次の整数に設置された給水所にはぴったり止まることはできませんでした。「まあこんなこともあるさ」と調和級数大好きカメさんは整数
の給水所を目指し再び歩き始めます。
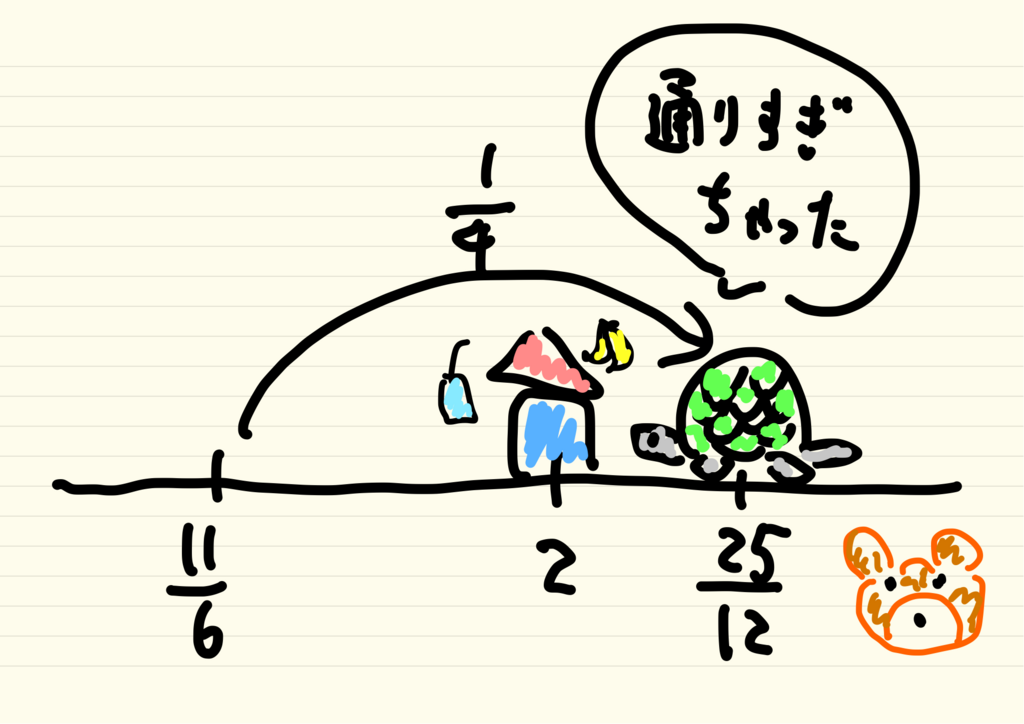
しかし、
なので、続く整数の給水所にもぴったり止まることはできず、整数
の給水所でバナナを食べなかったことを後悔し始めました。しかし「自分の歩幅はどんどん小さくなるんだ。次くらいにはぴったり整数の給水所に止まれるだろう。」と調和級数大好きカメさんは再び歩き始めるのでした。

しかしその後、調和級数大好きカメさんが整数の給水所にぴったり止まることは二度とありませんでした。。。
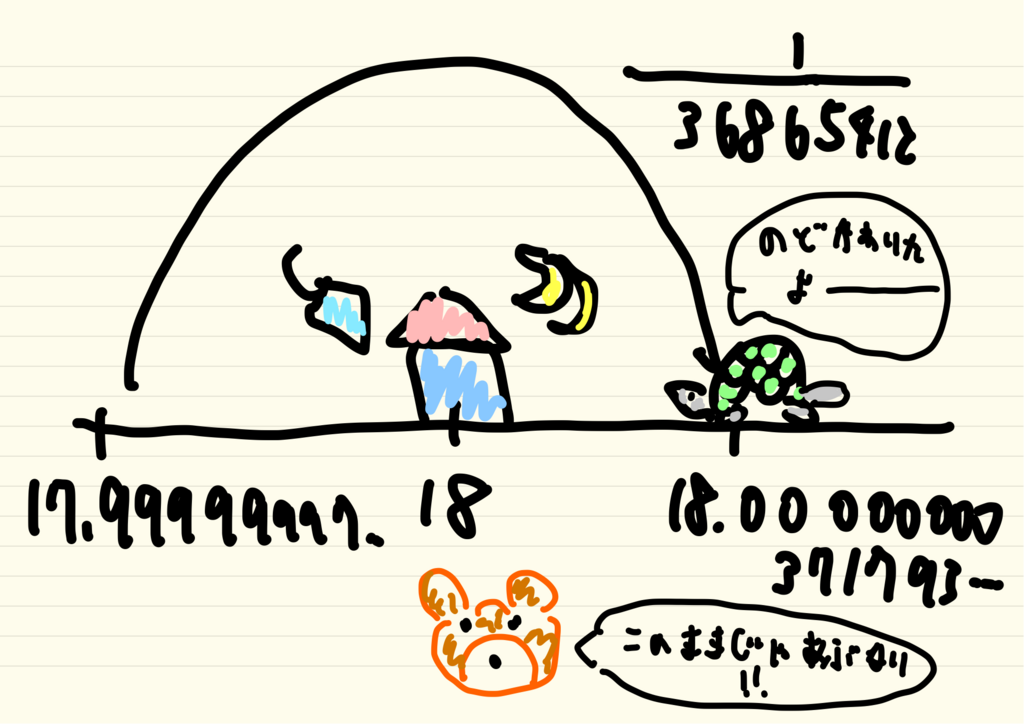
調和級数の途中和は整数にならない
実はのとき、
は整数になりません。
これは私は大学時代に読んでいた代数学のテキスト*1の演習問題で知りました。2016年11月、「これはあまり知られていなさそうだ。ブログに書いちゃおう!」と思い、この事実をブログに書いていたところ、あるブログが目に留まりました。
そうインテジャーズです。
証明はインテジャーズの記事を読んでください。「他のブログに書いてあることは書く意味がない(T T)」と、私のブログは書きかけのまま一年以上放置されていましたが、今回インテジャーズのアドベントカレンダーに投稿することで、日の目を見ることとなりました。
調和級数大好きカメさんに水を飲ませてあげたい
調和級数大好きカメさんの友達のくまさんは、とても友達想い。飲み食いせず歩き続ける調和級数大好きカメさんに提案をします。

くまさん「調和級数大好きカメさん。このままじゃ倒れちゃうよ。」
調和級数大好きカメさん「いいんだよ。僕はルール通りに頑張るだけだよ。僕は歩幅を変えるつもりもないし、整数以外の点で水を望んだり、バナナを望んだりしない。いくら給水所までの距離が以下だったとしても。」
くまさん「次の一歩で整数の給水所を超えてしまう時、歩幅を変えて歩いて給水所に止まろうよ。バナナ美味しいよ。」
調和級数大好きカメさん「僕は調和級数が大好きだ。歩幅を変えるなんて絶対にやりたくないんだ。わかってくれよ、くまさん。」
くまさん「違うよ。たしかに歩幅は変えるよ。でもそれはこの先君が歩む一歩の歩幅にするんだよ。つまり今歩こうとしている一歩を将来にとっておいて、将来歩く一歩の歩幅で今歩むんだよ。当然その歩幅は今歩いちゃうんだから将来は歩いてはいけないということにすればいい。とっかえっこするだけだよ。」
内心喉が渇いて、お腹も空いていた調和級数大好きカメさんは迷い始めます。
調和級数大好きカメさん「本当にそれで整数の給水所に止まれるの・・・?」
くまさん「止まれるんだよ。しかも全整数の給水所に!」
単位分数(エジプト分数)の話
調和級数の足し算に現れる分母が正の整数で分子がである分数を単位分数と呼びます。
や
等です。
そして、任意の有理数(=整数分の整数で表せる分数のこと。分数と思ってもらえればよい)は単位分数の和で表すことができるという素晴らしい定理があります。
証明はそうですね、インテジャーズを読んでください。
調和級数大好きカメさんが次の一歩で次の整数にある給水所を超えてしまう時、今調和級数大好きカメさんがいる点と、次の整数の給水所までの距離は有理数(≒分数)になっています。
つまりその有理数を単位分数の和で表すことで、調和級数の足し算に現れる分数でその距離を歩くことができるのです。
しかし、右辺の単位分数は今まで調和級数大好きカメさんが歩いた歩幅になっていてはいけません。調和級数大好きカメさんは歩幅の順番を変えることに関してはOKを出しつつありますが、同じ歩幅を歩くなんてことは彼のプライドが許すわけないのです。このままではカメさんが確実に次の給水所に止まれるという保証がありません。
しかしながら、を自然数として、実は次の式が成り立ちます。
なんと単位分数はそれより分母の大きい二つの単位分数の和で表すことができるのです。しかも無限通りに。当然単位分数の数はどんどん多くなります。
つまり、次の給水所のまでの距離を単位分数で表した時に、その単位分数に今まで歩いた歩幅が含まれている場合、上の式を使って別の単位分数で表してあげれば良いのです。単位分数の分母はどんどん大きく取ることができます。一方調和級数大好きカメさんが歩いた歩幅は高々有限通りです。単位分数を別の単位分数で表すという操作を繰り返せば、いつかは絶対に今まで歩いていない歩幅が出てくるのです。
最後の説得
くまさん「わかったよね?つまり次の一歩はこう決めるんだ。基本的に次の一歩はまだ歩いていない歩幅のうち最大のもので歩いてね。つまり、
〜
の歩幅で今まで歩いたことがあって、
の歩幅で歩いたことがないんだったら、次の一歩は
だ。」
調和級数大好きカメさん「うん。いつもそうしてきたよ。」
くまさん「でも、次の一歩で次の整数の給水所を超えてしまう時だけ、今君がいるところから次の給水所までの距離を単位分数の和で表すんだ。その単位分数に今まで君が歩いたことのある歩幅がある場合は、より分母の大きい単位分数の和で表してあげよう。いつしか君が歩いたことのない歩幅が現れるよ。そうしたらその単位分数たちを歩幅にして歩いていけばいい。ちゃんと給水所にたどり着けるから。」
調和級数大好きカメさん「そうだね。うん、そうするよ。ギリギリ僕のポリシーに反しない。」
くまさん「そう。ただし、自分が歩いた歩幅はちゃんと覚えておかないといけないよ。うっかり同じ歩幅で歩いてしまうといけないから。」
調和級数大好きカメさん「僕の記憶力が良いのは知っているだろう。僕がそんなドジを踏むと思うかいwww」
くまさん「ごめん。ちなみに、君は調和級数の順番を変えて歩くことになるんだけど、この順番を変える写像は全単射になっているよ。君は記憶力がいいから同じ歩幅を歩かない。つまり単射だ。そして、給水所を出発する時の次の一歩は確実にその時点で君が歩いていない歩幅で最大のものになる。なぜなら給水所から給水所まで一歩で行けるわけがないのだから。だから一つの整数を超えるごとにその時点で最大の単位分数を1つずつ消費することになるから、全射にもなるんだ。」
調和級数大好きカメさん「・・・ありがとう!」
こうして調和級数大好きカメさんは全整数で水を飲み、バナナを食べることができるようになりました。めでたしめでたし。

