血液型の割合に感じる神の意思

この記事は、日曜数学 Advent Calendar 2017 - Adventar 3日目の記事です。2日目は数学カフェの中の人さんの【日曜数学アドベントカレンダー2日目】2343の魅力を伝えたい。 - 数学カフェの中の人達のブログでした。ちなみに2343はスーパー合成数でした。

この記事の内容は今年6月に行われた第9回日曜数学会で発表した内容をまとめたものです。なお、今年開催された日曜数学会は全3回全て発表したので皆勤賞です！それでは始めます！

f:id:mattyuu:20171203102234j:plain

『血液型の割合に感じる神の意思』というタイトルで発表させていただきます。よろしくお願いします。

ツイッターのアンケートで血液型を聞くと本当にはA:B:O:AB=38:22:31:9になるのかな？レッツ検証♪投票したらRTお願いします(＞＜)
さっき投票日数間違えたので再投稿です💦#拡散希望RTおねがいします
— スモーキー💨 (@music_ine) 2017年2月28日

ある日twitterを見ていると、このようなアンケートが目に留まりました。
twitterには4択のアンケート機能がありますが、この機能を使って血液型のアンケートをとっています。「アンケート結果が日本人の血液型の割合と同じになるのか？」ということを調査しているようです。

f:id:mattyuu:20171203102237j:plain

最終票数は493票となっており、その結果を実際の日本人の血液型の割合と比べると、アンケート結果の血液型の割合と、日本人の血液型の割合がほぼ同じになっていることがわかります。数学的には大数の法則と言いますが、こんな単純な調査でも意図した結果が出てくるのは面白いですね。

生物学に疎い私はこの調査結果を見て、「日本人の血液型の割合はどのように決まっているのか？」と疑問を持ちました。しかも血液型の割合は国によって違うと聞いたことがあり、俄然気になります。

f:id:mattyuu:20171203102240j:plain

そこで日本以外の国の血液型の割合も調べて見ると、図中の円グラフのように確かに国によって血液型の割合はまちまちでした*1。ブラジルに至っては100%O型ということで驚きです。

f:id:mattyuu:20171203102243j:plain

以上が動機となり、今回の発表のテーマは『血液型の割合はどうやって決まるのか？』、『日本の血液型の割合は今後変わっていく可能性はあるのか？』としました。これらの疑問に数学を使って答えていきましょう！その結果、「神の意思」と呼んでも良いような事実に辿り着きましたので、紹介したいと思います。

f:id:mattyuu:20171203102246j:plain

まずはそもそも血液型とは何かを説明します。血液型を決める遺伝子(血液型遺伝子と呼ぶ)には、A型、B型、O型の３種類があり、人はその内の２つの遺伝子の組み合わせを持っています。血液型はA型、B型、AB型、O型の4種類だと思っていましたが、細かく言うとAA、AO、BB、BO、AB、OOの6種類があったのです。

ABO式血液型 - Wikipediaによるとこれら6種類のことを血液型ではなく遺伝子型と呼ぶようです*2。そしてAAとAOの遺伝子型をA型、BBとBOの遺伝子型をB型、ABの遺伝子型をそのままAB型、OOの遺伝子型をO型と決めています。AOをA型、BOをB型と呼ぶとO型遺伝子がかわいそうですが、O型遺伝子はA型、B型遺伝子に対して劣性遺伝子と言うそうで、生物学的にちゃんとした理由があるものと思われます。

f:id:mattyuu:20171203102250j:plain

次にお父さんとお母さんの血液型が赤ちゃんにどのように遺伝するのかを説明します。赤ちゃんは、お父さんが持っている2つの血液型遺伝子のうちどちらか一方を、そして、お母さんが持っている2つの血液型遺伝子のうちどちらか片方を、それぞれランダムに引き継ぎます。と言っても、実際に例を見た方がわかりやすいと思うので、2例出して説明します。

まずは1例目です。
この例ではお父さんはAAのA型、お母さんはBOのB型です。お父さんの遺伝子型はAAですので、赤ちゃんが引き継ぐのはA型の血液型遺伝子だけです。一方お母さんからは50%の確率でB型の血液型遺伝子を、50%の確率でO型の血液型遺伝子を引き継ぎます。よって赤ちゃんの血液型は50%の確率でAB、50%の確率でAOとなります。

f:id:mattyuu:20171203102254j:plain

次の例ではお父さんはABのAB型、お母さんはBOのB型になっています。先ほどの例と同様にお父さんからはA型、B型の血液型遺伝子を50%ずつの確率で、お母さんからはB型、O型の血液型遺伝子を50%ずつの確率でそれぞれ引き継ぐためそれぞれ25%の確率で、AB、AO、BB、BOの血液型を持った赤ちゃんが生まれてきます。

f:id:mattyuu:20171203102258j:plain

では、いよいよ数学を使ってモデル化していきましょう。血液型がAAの人の割合を $p_{\rm AA}$ という記号*3で表します。AOからOOまでの他の遺伝子型に対しても同様です。

これら6つの変数 $p_{\rm AA}$ 、 $p_{\rm AO}$ 、 $p_{\rm BB}$ 、 $p_{\rm BO}$ 、 $p_{\rm AB}$ 、 $p_{\rm OO}$ は割合を表しますから、当然それぞれの変数が実際にとる値は0以上1以下になります( $0\leq p_i \leq 1$ )。また、人の血液型はAA、AO、BB、BO、AB、OOのいずれかですから、6つの変数の和は1になります( $p_{\rm AA} +p_{\rm AO} +p_{\rm BB} +p_{\rm BO} +p_{\rm AB} +p_{\rm OO}=1$ )。

現在の日本だと、AAが8%、AOが31%、BBが3%、BOが19%、ABが10％、OOが29%となっているので、 $p_{\rm AA}=0.08$ 、 $p_{\rm AO}=0.31$ 、 $p_{\rm BB}=0.03$ 、 $p_{\rm BO}=0.19$ 、 $p_{\rm AB}=0.1$ 、 $p_{\rm OO}=0.29$ となります。

f:id:mattyuu:20171203102301j:plain

今回のテーマに『日本の血液型の割合は今後変わっていく可能性はあるのか？』という疑問を掲げています。先ほど血液型の割合を変数( $p_i$ )で表しましたが、これに加えて変数の時間変化も考える必要があります。

そこで、ある世代の血液型の割合( $p_i$ )を入れると、次の世代の血液型の割合( $p_i^{+}$ )を返すような関数 $F$ を作りたいと思います。 $F$ が作れると、ある世代の血液型の割合に次々と $F$ を作用させる事で血液型の割合の変数の時間変化がわかるのです。

f:id:mattyuu:20171203102305j:plain

$F$ を構成するに当たって3つの前提があります。

まず1つ目は『結婚相手は血液型で選ばない』という事です。血液型の相性という話も聞くため、中には結婚相手を血液型で選ぶ人もいるかもしれませんが、大半の人は血液型では相手を選ばないでしょう。マクロな視点で見たら結婚相手の血液型の確率は現在の血液型の割合に平均化されるという事です。

2つ目の前提は、『どの血液型の組み合わせのカップルも平均して同じ数の子供を出産する』です。夫婦によって子供の数はまちまちですが、その数は夫婦の血液型に依らないだろうという前提です。「あの夫婦はA型同士なので子沢山だわね」というような話は聞いたことありませんので、これも自然な前提かと思います。

3つ目の前提は『時間軸に世代という明確な区切りがあるものとする』です。今の日本には0歳児から100歳を超える御高齢の方まで連続的に各年齢の人が暮らしていますが、祖父母世代、父母世代、子供世代というように世代が存在することを前提にします。今の子供世代が次世代の父母世代となり赤ちゃんを産む事で次の子供世代が誕生し、また次の世代では最初の子供世代の人たちは祖父母世代となり、先代で誕生した子供世代が父母世代となり新しい子供世代が誕生します。前2つのものに比べて少し重たい前提ではありますが、暖かく見守ってほしいです。 $F$ は父母世代の血液型の割合から、次の子供世代の血液型の割合を与える関数になるのです。

さて、モデルと前提が準備できましたので実際に $F$ を構成していきます。

f:id:mattyuu:20171203102313j:plain

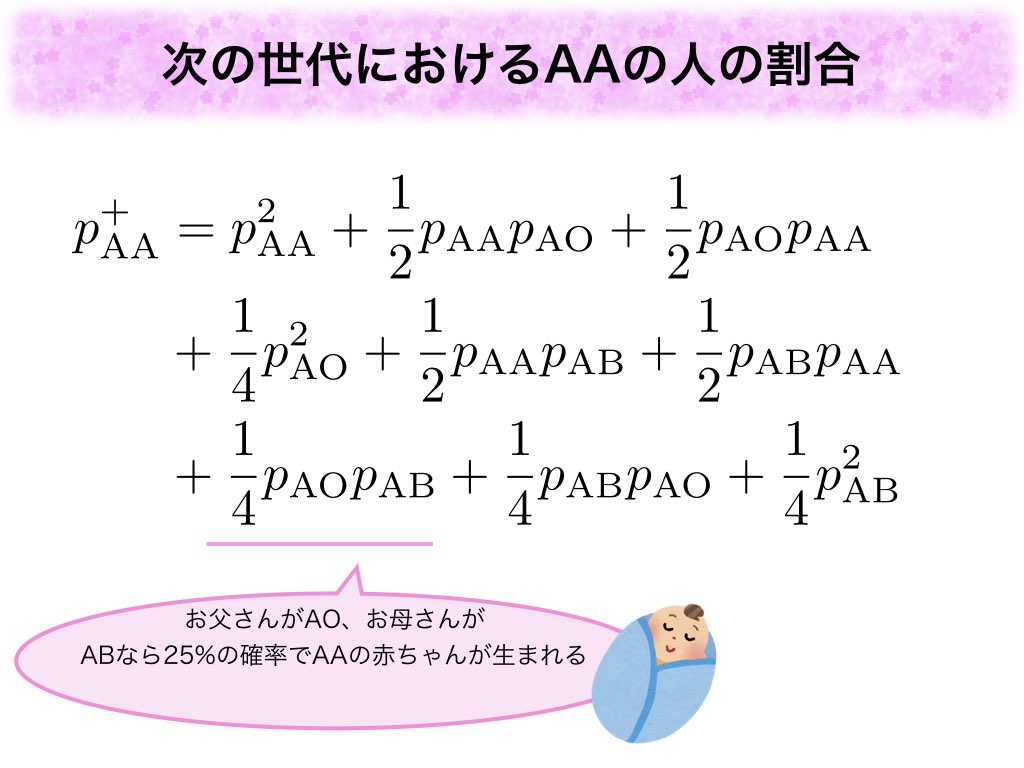
こちらが次の世代のAAの血液型の割合 $p_{\rm AA}^{+}$ を与える数式になります。
まず、右辺の $\frac{1}{4}p_{\rm AO}p_{\rm AB}$ について説明します。
夫婦をランダムに選んだ時に、お父さんがAO、お母さんがABである確率は $p_{\rm AO}p_{\rm AB}$ となります*4。そして、この夫婦の赤ちゃんの血液型がAAになる確率は25%(=1/4)です。これから父母世代のAOのお父さん、ABのお母さんが次の世代のAAの割合に寄与する大きさは $\frac{1}{4}p_{\rm AO}p_{\rm AB}$ となるのです。

赤ちゃんの血液型がAAということは、お父さん、お母さんの血液型の組として考えられるのは、(AA,AA)、(AA,AO)、(AO,AA)、(AO,AO)、(AA,AB)、(AB,AA)、(AO,AB)、(AB,AO)、(AB,AB)のいずれかです。お父さんの血液型がBO、お母さんの血液型がABであればどう頑張ってもAAの血液型を持つ赤ちゃんは産まれてこないため、(BO,AB)は考える必要はありません。(AO,AB)以外にも同様に計算していって全て足すこと*5で次の世代のAAの血液型の割合を出せるのです。

f:id:mattyuu:20171203102309j:plain

同様に計算すると次の世代のAO、BB、BO、AB、OOの血液型の割合を導出する式はこちらになります。目が回りそうです。。。簡単に書けないでしょうか。。？

f:id:mattyuu:20171203102316j:plain

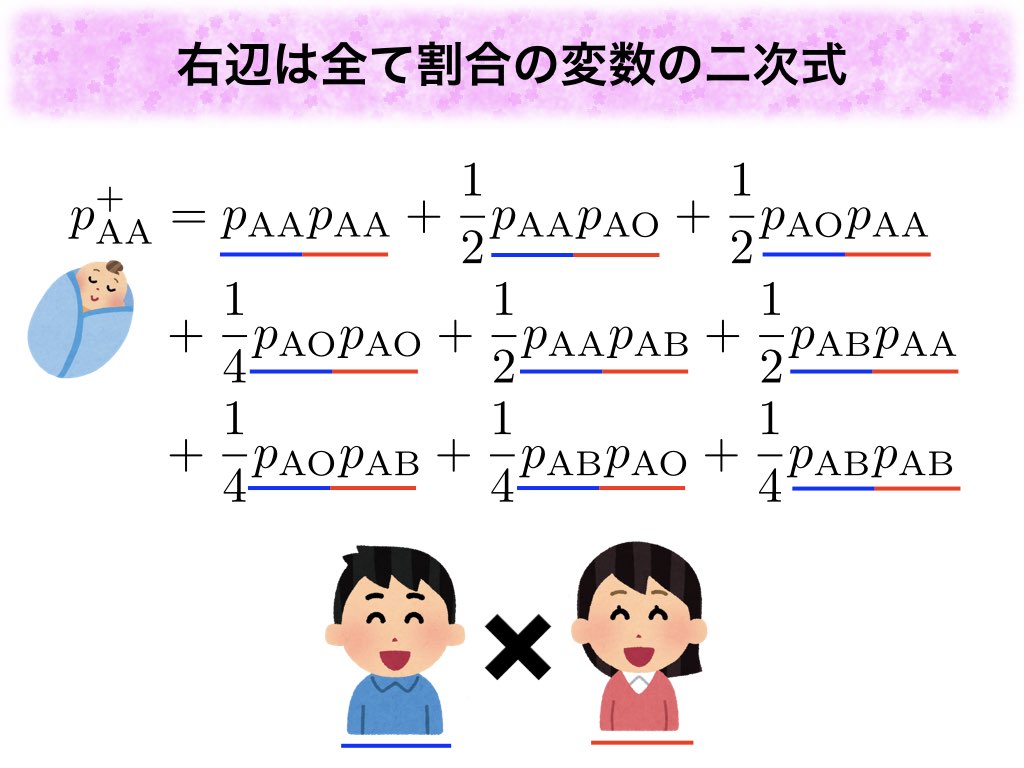
よく見ると、右辺は変数の二次式になっています。今まで $p_{\rm AA}^2$ と書いてあったところも $p_{\rm AA}p_{\rm AA}$ と書くことで、左の $p_i$ はお父さん達の、右の $p_j$ はお母さん達の血液型の割合のように見えてきませんか？

f:id:mattyuu:20171203102323j:plain

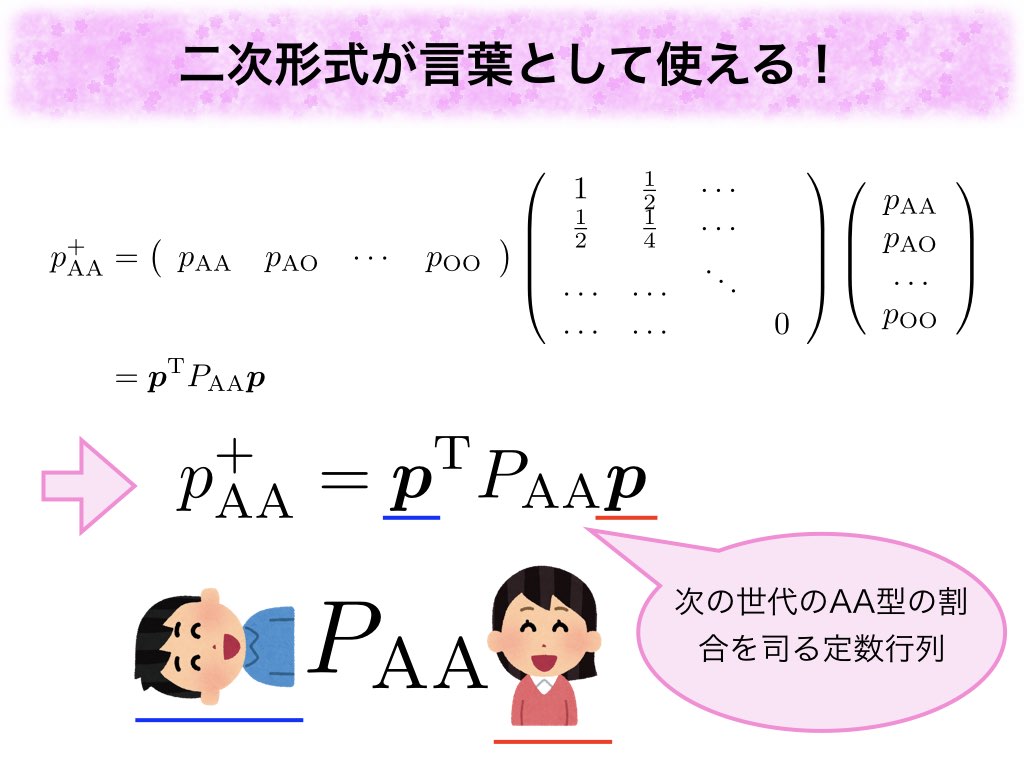
知らない方はご勘弁ですが(大半かもしれません...)、二次式は大学初年度で習う線形代数の二次形式(二次形式 - Wikipedia)という言葉を使えば、ベクトルと行列を使って簡単に書き表すことができます*6。ベクトルはお父さん、お母さん世代の血液型の割合、行列はAA、AO、BB、BO、AB、OO それぞれに固有な定数行列となります。

例えば次の世代のAAの割合( $p_{\rm AA}^{+}$ )は簡単に $p^{\rm T}P_{\rm AA}p$ と書けます。複雑な係数たちは $P_{\rm AA}$ という定数行列が中に閉じ込めてくれています。 $P_{\rm AA}$ は何も悪いことしていないのに、一身に面倒なものを全て抱え込んでくれております。そういった意味で私は $P_{\rm AA}$ を次の世代のAA型の割合を司る定数行列と呼んで崇めています。

f:id:mattyuu:20171203102327j:plain

他の血液型の割合を司る行列たちはこのようになっています。みんなありがとう。

f:id:mattyuu:20171203102320j:plain

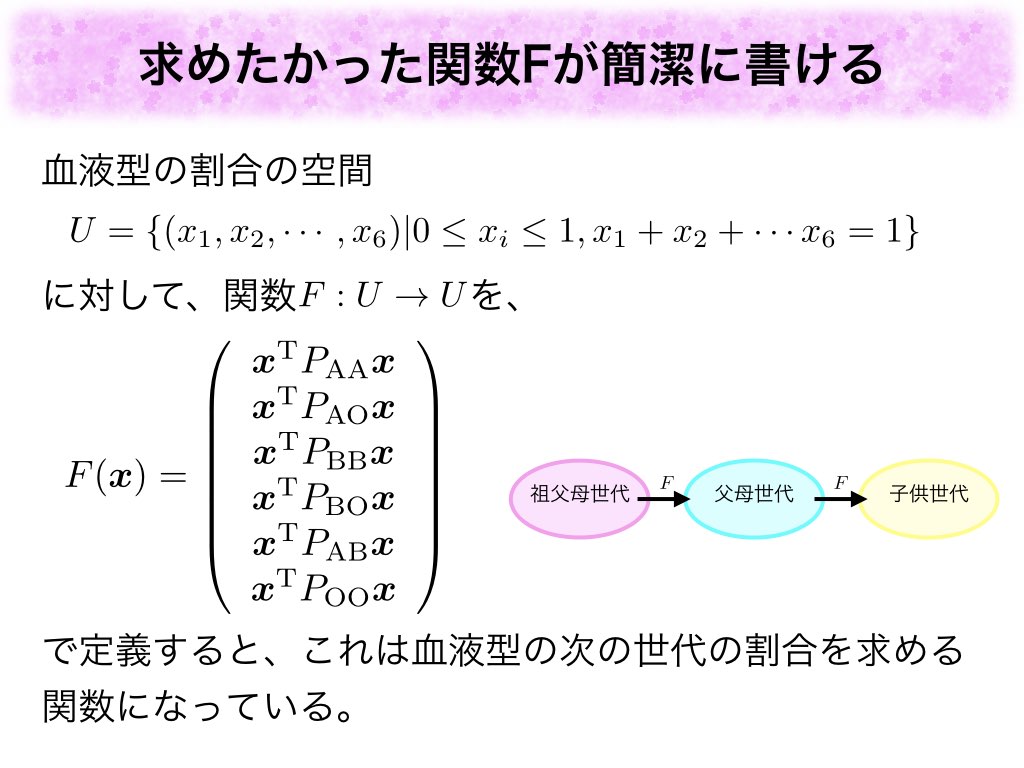
さて、 $P_{\rm AA}$ 〜 $P_{\rm OO}$ のおかげで関数Fをこのように簡単に書くことができます。二次形式に慣れていない方は前述した二次式と全く等価ですので無理に理解する必要はありません。

f:id:mattyuu:20171203102331j:plain

今回のテーマを再掲します。『血液型の割合はどうやって決まるのか？』に対しては関数 $F$ が定まったので済みとします。 $F$ があれば原始時代の血液型の割合から、後の世代の血液型の組が全てわかるからです。

次に『日本の血液型の割合は今後変わっていく可能性はあるのか？』について考えます。

f:id:mattyuu:20171203102336j:plain

今の世代と次の世代で血液型の割合が変わらないということは、今の血液型の割合に $F$ を作用させても同じ割合が出てくることを意味します。血液型の割合がこのような条件を満たすとき、今後も割合が常に一定ということで「定常状態」と呼ぶことにします。

f:id:mattyuu:20171203102340j:plain

前述した通り現在の日本では、AAが8%、AOが31%、BBが3%、BOが19%、ABが10％、OOが29%となっているので、 $p_{\rm AA}=0.08$ 、 $p_{\rm AO}=0.31$ 、 $p_{\rm BB}=0.03$ 、 $p_{\rm BO}=0.19$ 、 $p_{\rm AB}=0.1$ 、 $p_{\rm OO}=0.29$ です。日本の血液型の割合が今後も変わらない、つまり定常状態になっていることを確かめるためには、これらの割合の組に $F$ を作用させて割合が変化しないことを確認すればいいのです。

f:id:mattyuu:20171203102344j:plain

実際に計算して見るとこの通りほぼほぼ変わりませんでした！普通なら「日本人の血液型の割合は今後変わらないことがわかったぞ！」と喜びたいところですが、血液型の割合が変化していないということはなんとなくわかっていたことなので、このモデルの妥当性が示されたということで喜びたいと思います。

ただし、今後外国の方の移住が進んで血液型の割合に変化が出たり、「B型結婚禁止法」、「A型子供4人産むこと義務法」等前提条件が崩れるような意味のわからない法律が策定された場合は再度モデル作りが必要になります。

f:id:mattyuu:20171203102348j:plain

ここまでで残っていたテーマ『日本の血液型の割合は今後変わっていく可能性はあるのか？』も解決しました。最後に私が気づいた神の意思と呼べるようなものを紹介したいと思います。

f:id:mattyuu:20171203102206j:plain

当初の予想では原始時代の血液型の割合がわかれば、 $F$ を作用していくことによって血液型の割合が変遷し、最終的に定常状態に落ち着くのであろうと予想していました。

f:id:mattyuu:20171203102210j:plain

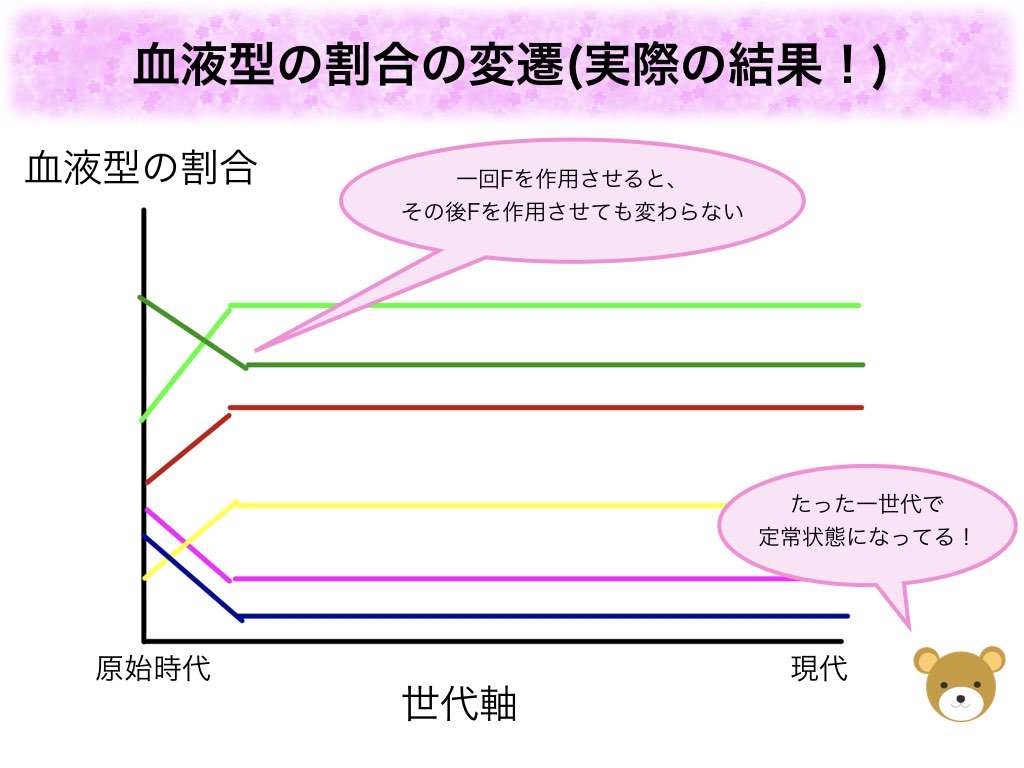
しかし実際にいろいろな初期値(原始時代の血液型の割合)を入れてシミュレーションしたところ、たった1回 $F$ を作用させるだけで定常状態になることがわかりました。これは驚きです！

シミュレーション結果だけではなく、変数 $p$ を文字で置いて、 $F(F(p))$ と $F(p)$ が一致することを確認しているので、これは数学的な事実(定理と言ってよい?)です。 $F(F(p))$ に対して、 $P_{\rm OO}=1-P_{\rm AA}-P_{\rm AO}-P_{\rm BB}-P_{\rm BO}-P_{\rm AB}$ を入れることで、うまいこと4次の項が消えて $F(p)$ になることが確認できます。ちょうど良い計算練習になるので、興味がある方は計算してみてください。

f:id:mattyuu:20171203102213j:plain

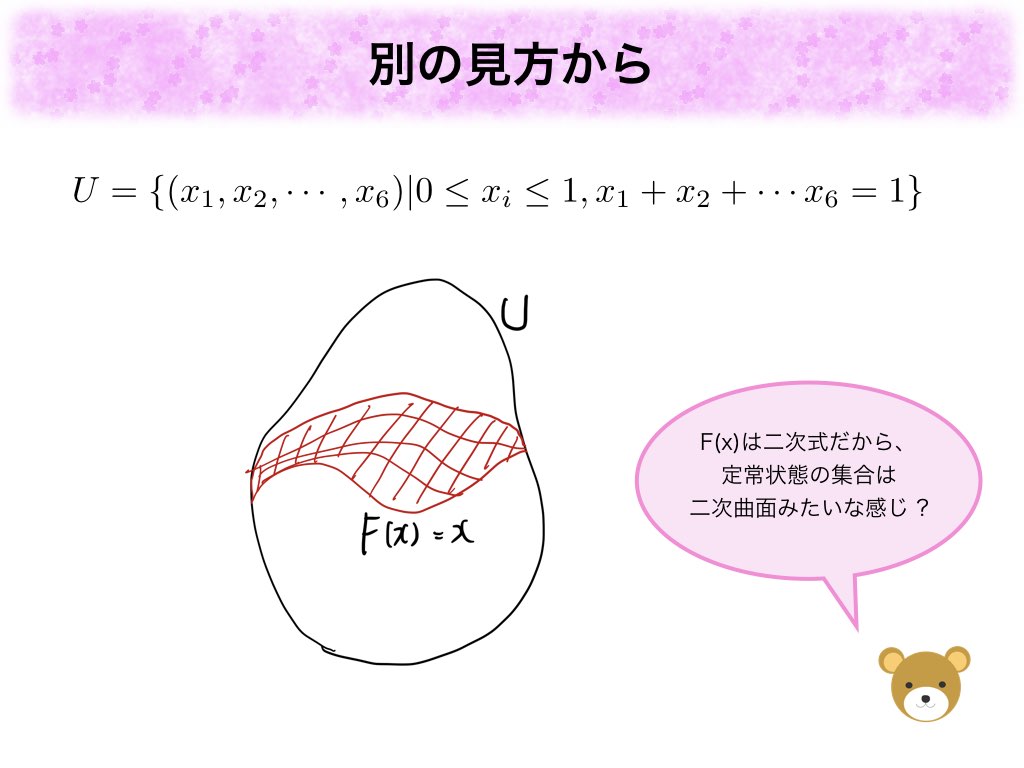
この発見を別の見方でも解説します。まず $U$ という血液型の割合の空間があった時に、この血液型の空間において定常状態となる血液型の割合の集合(つまり、 $F(x)=x$ を満たす $U$ の元全体)を考えます。

$F(x)$ は二次式なので二次曲面(二次曲面 - Wikipedia)のようになるかと思いますが、6次元空間なので図示できません。。。図の赤いところが定常状態の集合のイメージです。

f:id:mattyuu:20171203102216j:plain

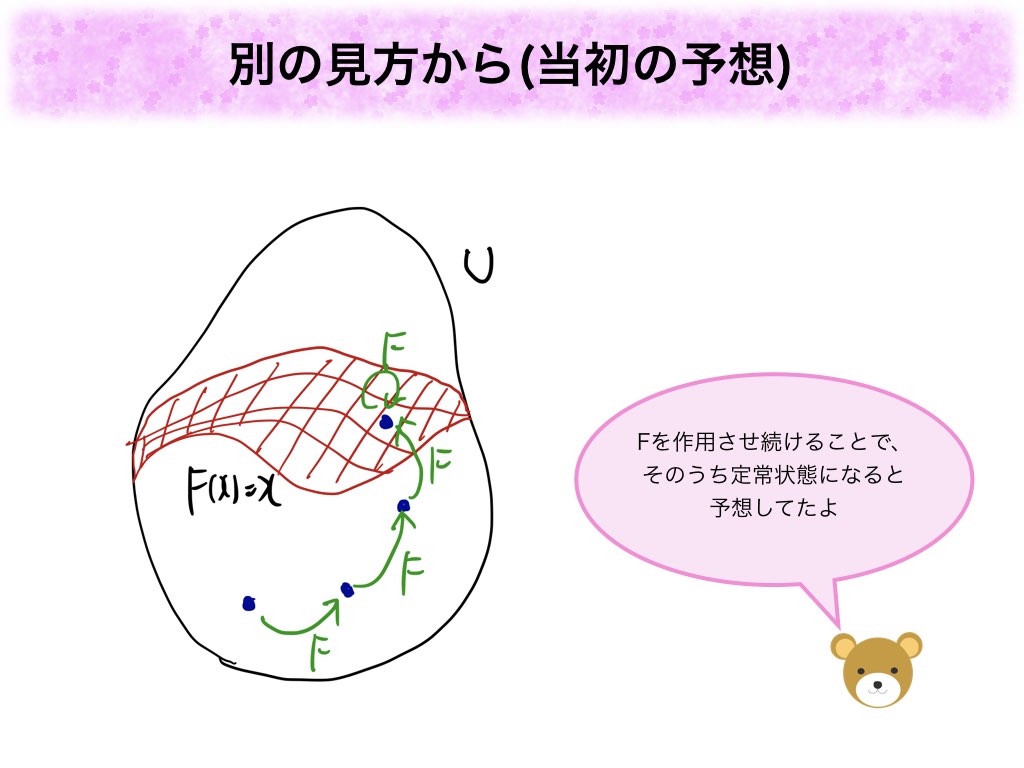
当初の予想では、 $U$ に任意の点(初期値)を選ぶと、 $F$ を作用させるにごとに点が移動していき、いつかは定常状態の赤い面に辿りつき、それ以降は $F$ を作用させても動かない、となると思っていました。

f:id:mattyuu:20171203102219j:plain

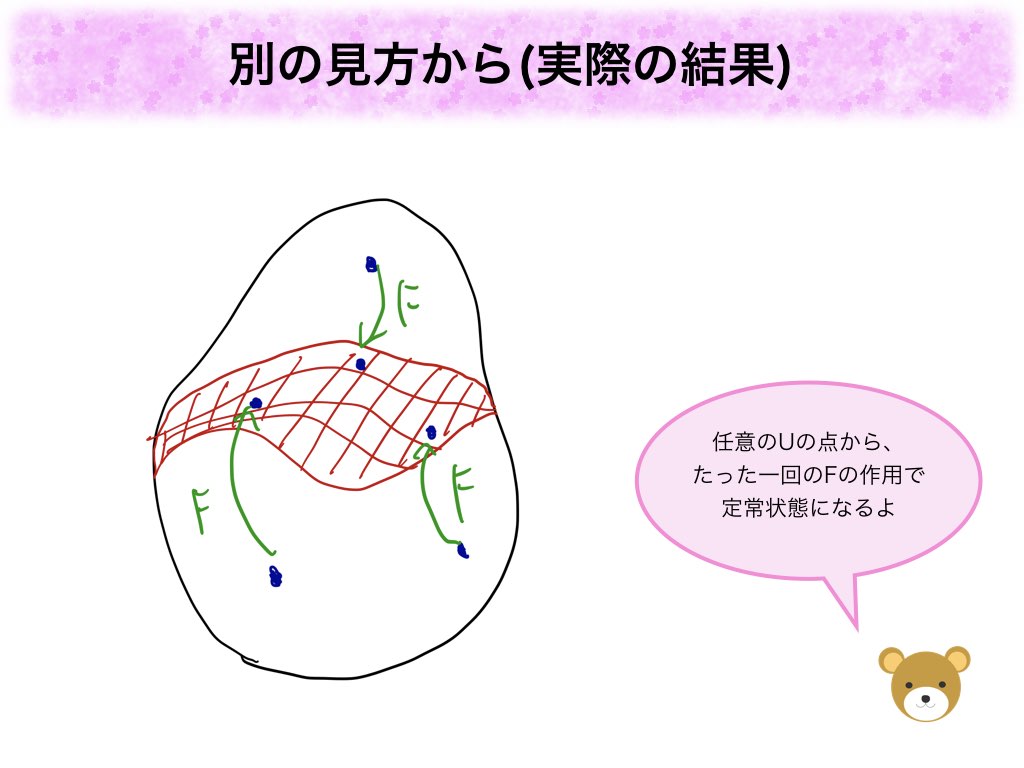
しかし実際にわかったことは、 $U$ のどの点を出発点にしても、たった1回 $F$ を作用させることで定常状態の赤い面に辿りつき、それ以降は $F$ を作用させても動かないというものでした。なんとも驚きです！

f:id:mattyuu:20171203102224j:plain

これはまさしく血液型の割合を安定させようという神の意思ではないでしょうか？生物学は疎いのですが、自然が作り出したものだけあって数学と同じく非常に美しく感じます。

実はこの内容を日曜数学会以前にもクローズな場で発表したことがあるのですが、発表後、聴講者の方から「これはハーディー・ワインベルクの法則(ハーディー・ワインベルクの法則 - Wikipedia)というものだよ。」と教えていただき、驚きました。リーマン予想への挑戦やラマヌジャンを見つけ出したことで有名なハーディーが、このような生物学の法則に関しても言及していたのです！そして私の前提もハーディー・ワインベルクの法則の前提と共通する部分が多々あり、「自分すごい！」と思いました。

数学では証明はできても、なんか不思議と感じることは山ほどあります。例えば、 $\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$ などは証明を読めば成り立つことがわかりますが、なぜ突然 $\pi$ が出てくるのか、なんで $6$ なのか等不思議は尽きません。今回の神の意思も同様で、任意の $p$ に対して $F(F(p))=F(p)$ となることは確認しましたが、なぜこんなことが成り立つのか？血液型を司る行列たちにどんな秘密があるのかはわかっていません。一時期躍起になって挑戦しましたがわかりませんでした。血液型遺伝子がAとOしかない場合でも試しましたがやはり同様に成り立ったため、血液型遺伝子の種類が増えても成り立つと予想します。

と言うことで次の問題を投げかけて本記事を締めくくりたいと思います。誰かわかったら教えてくださいm（　）m

誰か解いて問題
$U=\{x \mid 0\leq x_i \leq 1, \sum x_i=1\}\subset {R}^n$ と $n$ 次の対称行列 $P_1,\cdots ,P_n$ に対して、関数 $F\colon U\rightarrow U$ を次式で定義する。
( $F(x)$ の第 $i$ 成分) $=x^{{\rm T}}P_ix$
この時、任意の $x\in U$ に対して $F(F(x))=F(x)$ が成り立つような $P_1,\cdots,P_n$ の性質の必要十分条件を与えよ。

f:id:mattyuu:20171203102228j:plain

*1:血液型の割合に関しては、下記のサイトを引用しました。uranailady.com

*2:2つの血液型遺伝子の組AA、AO、BB、BO、AB、OOは本来きちんと遺伝子型と書くべきですが、説明がしにくくなるので、今後これらも広い意味で血液型と書く事にします。

*3:以下、変数と呼びます。

*4:ここで結婚相手は血液型で選ばないという前提が効いています。

*5:お父さん、お母さんの血液型の組に対して何も重み付けせず足すことができるのは、2つ目の前提『どの血液型の組み合わせのカップルも平均して同じ数の子供を出産する』によるものです。

*6:ちょうどこの数式を考えていた頃、別件でガウス整数論の二次形式を読んでいたので「うぉー二次形式すごい！」となった思い出があります。ガウス整数論の二次形式はベクトル、行列の成分は整数の範囲の話になるため、これでもかというくらい全く別の数学です。

mattyuuの数学ネタ集

世界は数式で溢れている

血液型の割合に感じる神の意思