はじめに
先日職場の勉強会でRSA暗号、楕円曲線暗号について発表をしました。面白いことに話の全体を通してフェルマー(17世紀のフランスのアマチュア数学者)が登場しました。
- RSA暗号の鍵となる素数の面白い性質としてフェルマーのクリスマス定理(4で割って1余る素数が2つの平方和であらわせるやつ。
等) の紹介。
- RSA暗号で平文、暗号文を変換するアルゴリズムの原理の証明にはフェルマーの小定理を使う。
- 楕円曲線はフェルマーがそれと知らず(?)好んで研究の対象にしていた。
- 「楕円曲線はモジュラーである」という谷山–志村予想(の特赦なケース)を証明することでフェルマーの最終定理が証明された。
フェルマーはパスカルと共に確率論を創始するなど、上記の暗号関連の話以外にも重要な仕事を行なっております。フェルマーは17世紀の人ですが、現代社会の根っこの部分に彼が与えた、与えている影響は大きそうです。ただ、今回はこれ以上フェルマーの話はしません。勉強会の資料作成を通して、有限体上の楕円曲線を可視化したのですが(←グラフ書いただけですが)、可視化した楕円曲線を眺めたり、いじったりしているうちに、「パズルとして売り出せるんじゃない?」というような面白い性質を見つけたのでその紹介をしたいと思います。
まず、楕円曲線とは下記で定義されます。
、
を定数とし、方程式
を満たす全体の集合(←グラフと呼ぶ)を楕円曲線という。
注1:この記事では上記の一般形を得るために、標数が2、3以外の体上で考えています。
、
も
の元です。
注2:(右辺のxの3次式)=0は重解を持たないものとします。
中学校や高校で習う関数のグラフは、実数体()という足し算、引き算、掛け算、割り算ができる世界*1の上で考えています。実数上で楕円曲線のグラフを描くと、例えば下記の図のようになります。
、
の場合

、
の場合
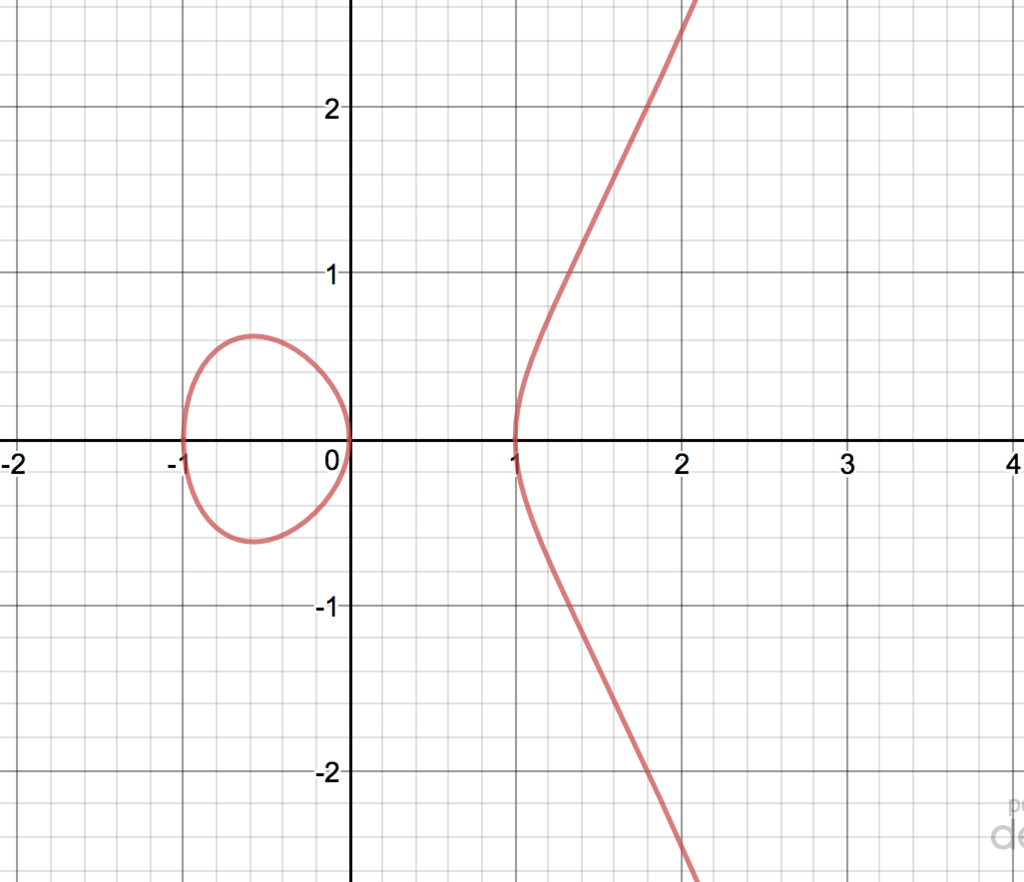
2つ目の、
)の例でグラフの描き方を簡単に説明します。
のときは、
となりますから
です。
に赤い点を描きます。同様に
、
のときも
となるので、
、
にも赤い点を描きます。
のときは、
となるので、
です。
、
に赤い点を描きます。先程と違い、1つの
に対して2つの
が対応しました。
のときは、
となるので、これを満たす実数
は存在しません。そのため実数上のグラフでは
のときは描く点はありません。
を
から
まで動かしながら、各
に対して方程式を満たす
を同様に求めて
に点を描いていくと、先程の2つ目のグラフになるのです。
有限体 上の楕円曲線
上の楕円曲線
楕円曲線暗号では、楕円曲線は実数体()上ではなく、有限体
上で考えます。有限体
が何かわからない方は以前書いた下記の記事を読んでみてください。
は簡単に言えば集合
に適切に足し算、引き算、掛け算、割り算を定義した世界になります。今回の記事では足し算と、掛け算しか使わないため、例として
の足し算表、掛け算表を載せておきます。
足し算表
| + | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
掛け算表
| × | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
有限体の復習が終わりましたので、実際に
上の楕円曲線を描いてみましょう。ここでは例として
、
、
とします。
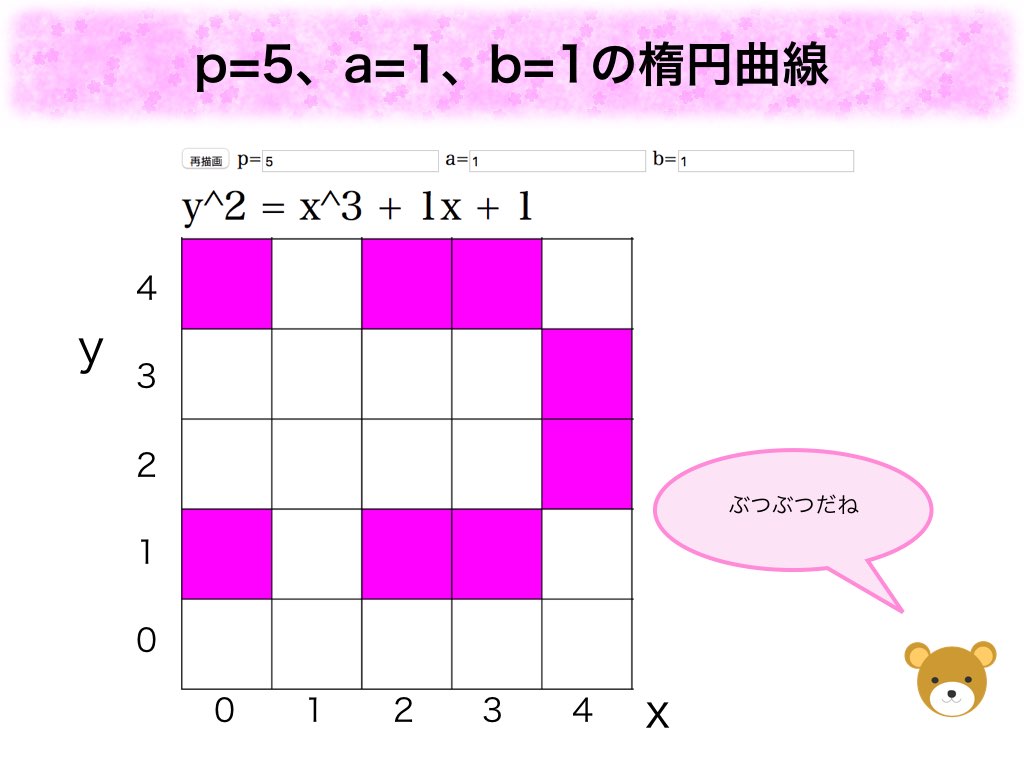
楕円曲線というのに、グラフは繋がってないし、曲がった感じもしませんが、楕円曲線の定義に反してませんし、描き方も実数体上の時と全く一緒です。実数体ではから
までの無限個の
に対して、
を求めないとグラフは描けませんでしたが、有限体
上では
個の
に対して
を求めればよいことが本質的に異なります。
では実際に上のグラフがのグラフになっていることを確認してみましょう。
のとき、
となるので、2乗して
になる数求めればよいことになります。
上では
、
、
、
、
より、
のときは
、
となります。よって
と
のマスにピンク色を塗っております。
同様に例えばのとき、
となります。
上では
、
より、
と
のマスにピンク色を塗ります。
様子が違うのはのときです。このとき
となりますが、
上では2乗して
になる数は存在しません。そのため
の縦列のセルにはピンク色に塗るセルはありません。これは先述した実数体上の楕円曲線の例で、
の解が存在せず描く点がなかったことと同じです。
今回有限体上の楕円曲線はjavascriptでプログラムを作って描画しています。プログラムの良いところは一回プログラムを作ってしまえばパラメータ(ここでは、
、
)を変えたグラフも容易に描画できることです。手計算、手描きでグラフを作成すると、パラメータを変えるごとに改めて計算を行う必要があります。また
を大きくすると計算自体が大変になります。
さあプログラムの利点を活かして上の楕円曲線'を全て描画してみましょう。
、
はそれぞれ
の5通りから選ぶことができるので、全部で25通りの楕円曲線'が得られます。
上の楕円曲線'たち

にしても描けます!
上の楕円曲線'たち(出力結果を一部抜粋、実際には
通りの楕円曲線'が現れます。)
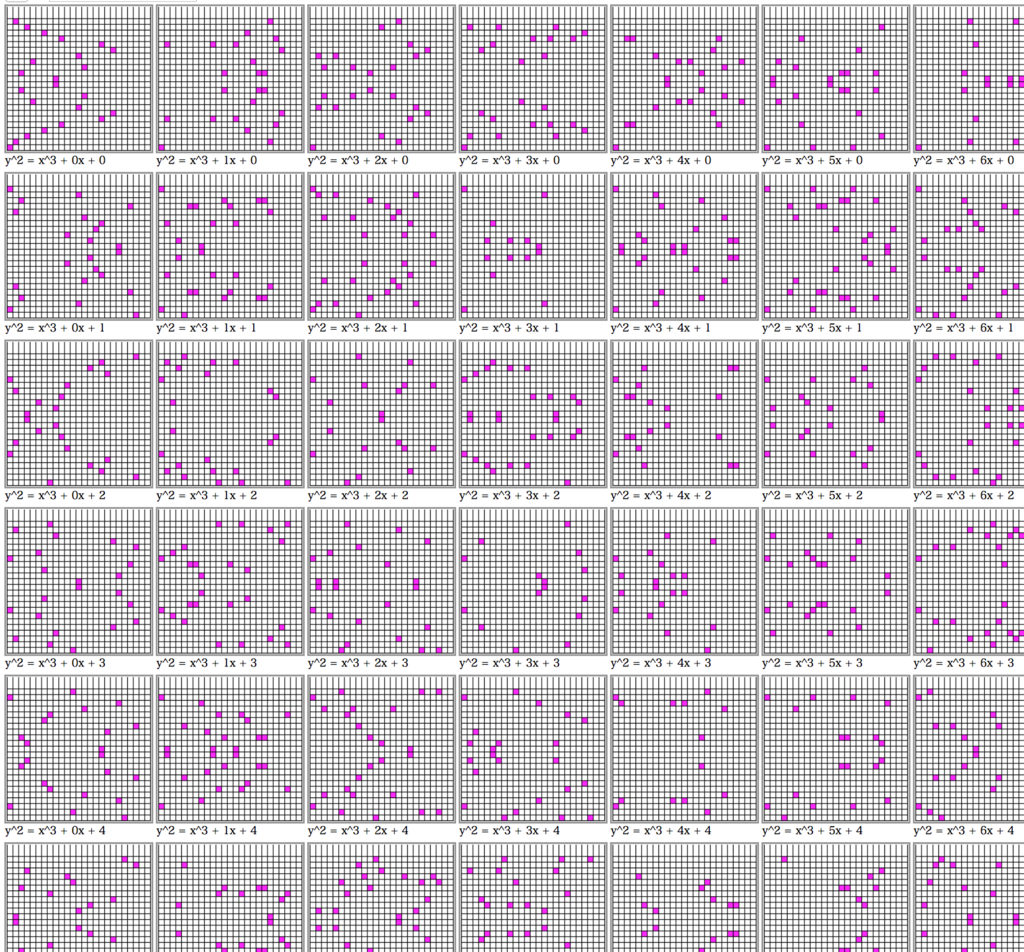
はぁはぁ、、楽しい。。
ここで一点白状します。上記には楕円曲線以外のグラフも含まれています。楕円曲線の定義の注2で記載しましたが、の右辺の
の3次式について、(右辺のxの3次式)=0という方程式を作ると、この方程式は重解を持たないという前提があります。例えば
上では
となり、重解を持ってしまうので、
上で
は楕円曲線ではありません。
しかし、今回考えたパズルは全ての、
を対象にしないと成立しません。誠に情けないですが楕円曲線の集合に、楕円曲線とは言ってはいけない
上の
といった曲線も追加して楕円曲線'という名前で広い範囲の集合を考えます。
気づいた性質
さて、楕円曲線'のグラフを並べてみると気づくことがあります。それは、
を固定して、
を
から
まで動かした
個のグラフを重ね合わせると全マスがちょうど1回ずつピンク色に塗られるのです!
言葉だけではわからないと思いますので、つまりこういうことです。

つまり、こういうことです。
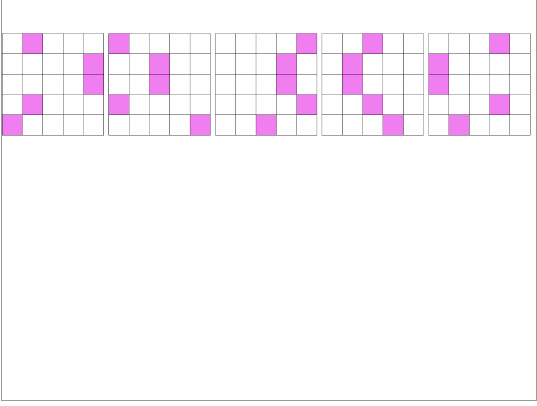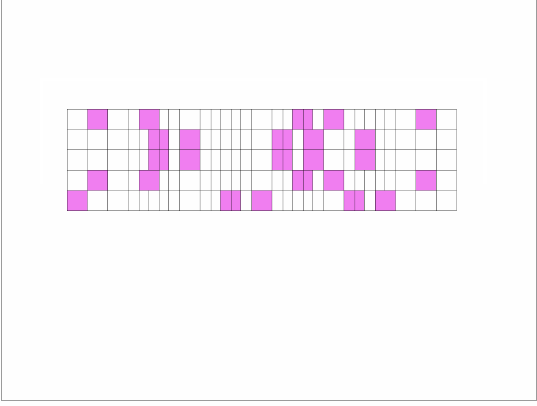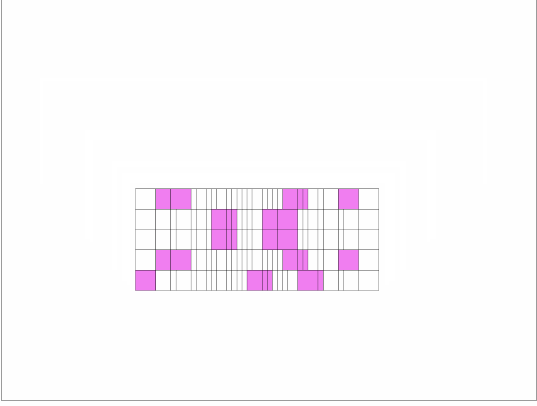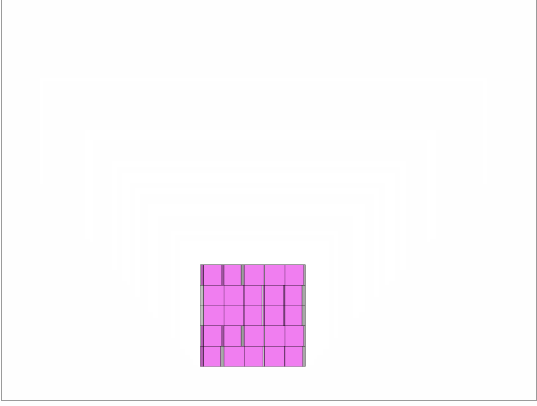
つまり、こういうことです。
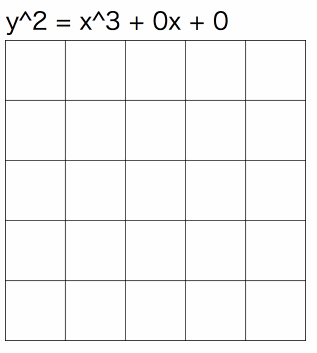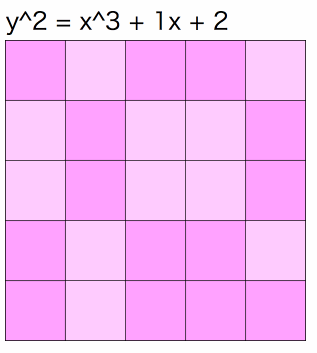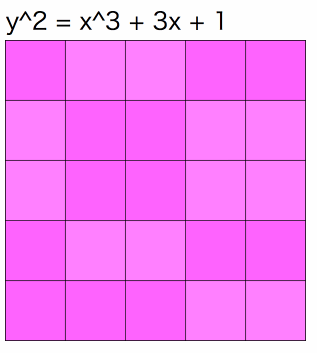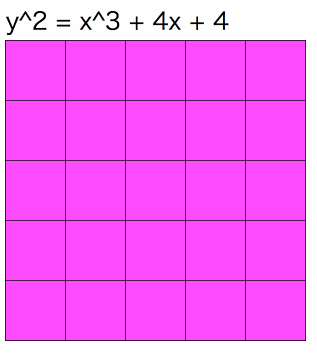
最後の例ではピンク色の部分はセロハンのような素材と思ってください。セロハンを重ねるごとにピンク色が濃くなります。が同じ値の時は各セルが足並みをそろえて濃くなっていく様子が確認できます。
でも、綺麗に成り立ちます。(ファイルサイズが大きくなってしまうので、アニメは途中で止めています。)
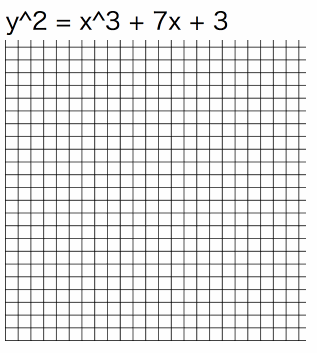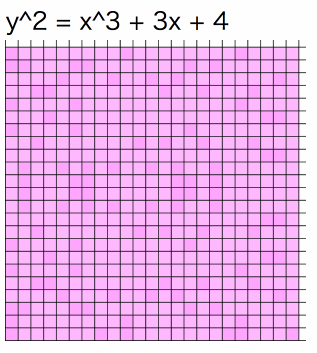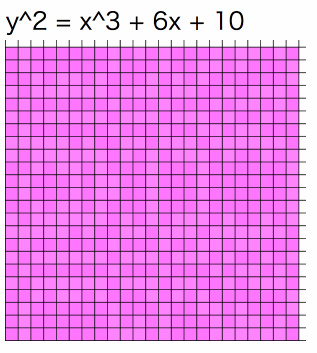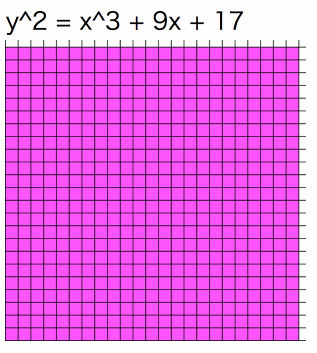
はぁはぁ、、面白い。。
とか、
とかもっと大きい素数では楕円曲線'のグラフもより複雑になります。複雑なグラフが
個あり、それを重ね合わせると綺麗なピンク一色!何かに役立つわけではないですが、数学の力を感じさせられます!
この性質が成り立つ証明は超簡単です。残念ながらこの性質は楕円曲線ではない方程式でも成り立ちますし、もっと言えば体上じゃなく剰余類環
上でも成り立ちます。
上の楕円曲線':
に対して
を1つ固定する。この時、下記2点を示せばよい。
に対して、
で
となる。
のとき、
、
は共通の解を持たない。
- 1の証明:
とすればよい。
- 2の証明:
が共通の解とすると、
、
がそれぞれ成り立つ。辺々を引くと、
となり、これは前提に矛盾。
証明はいかにも当たり前ですが、可視化してみないと気づかなかった性質なので、満足感はあります。
応用例
楕円曲線'に関して面白い性質を見つけたので、何か応用したくあります。
まずは、大人向けのパズルとして活躍の余地はないでしょうか。のときは、25種類の楕円曲線'が描かれたカードを用意します。色が塗られていない部分は透過するようにしたいためアクリル板で作成しましょう。25枚のカードから適切に5枚ずつ選んで、それぞれの組で各カードを適切に回転、反転させて重ね合わせることで、ピンク一色のカードの組が5セットできたら成功です。*2

が余裕でできるようになったら、
、
と難易度を上げていけば素数の数だけ楽しめます!
次に思いつくのは子供向けの絵合せパズルです。2〜3歳の時はを固定して、5枚のカードでくまさんの絵合せをしましょう。
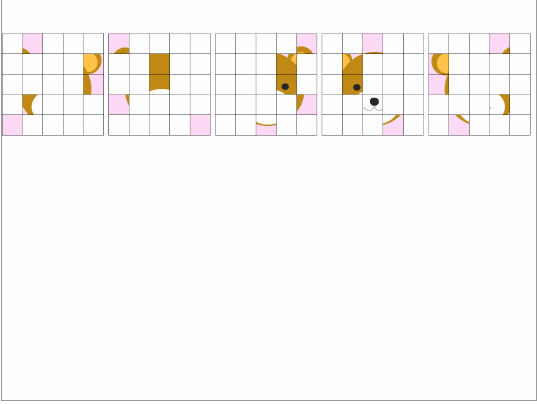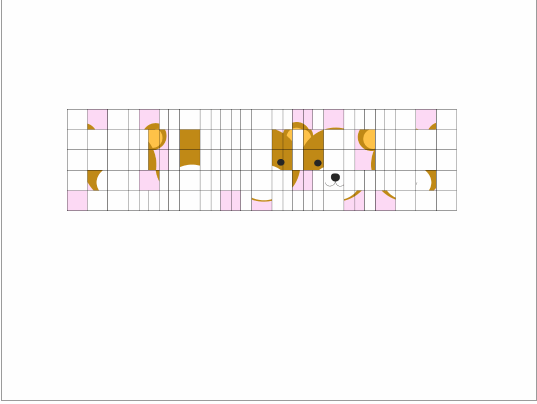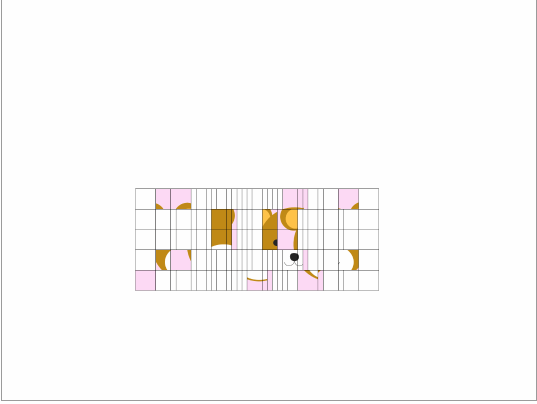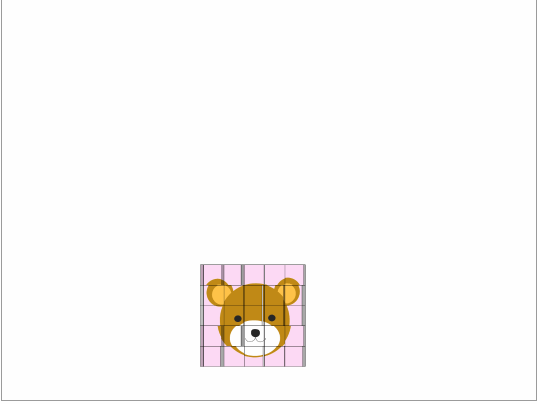
幼稚園に行きだしたら、ゴレンジャーを題材にしましょう。この頃になると25枚あっても大丈夫なはずです。
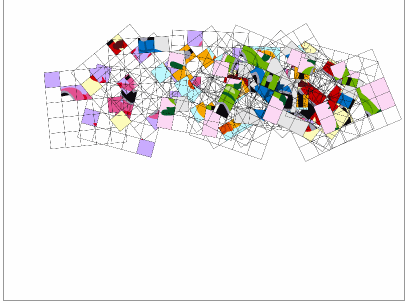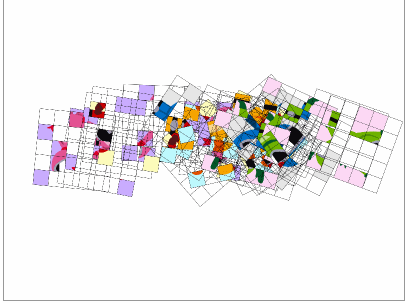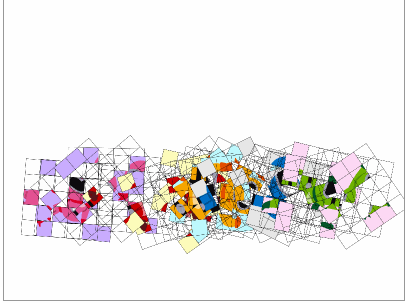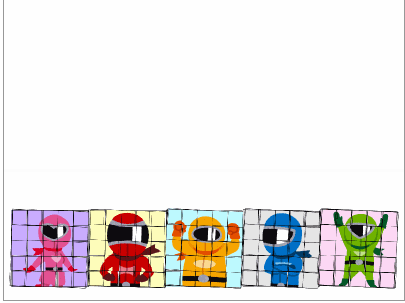
このように子供の時から素数や楕円曲線'に慣れ親しみ純粋に育った男の子は、プロポーズにもメッセージカードと称して楕円曲線'カードを使用してしまう恐れがあります。
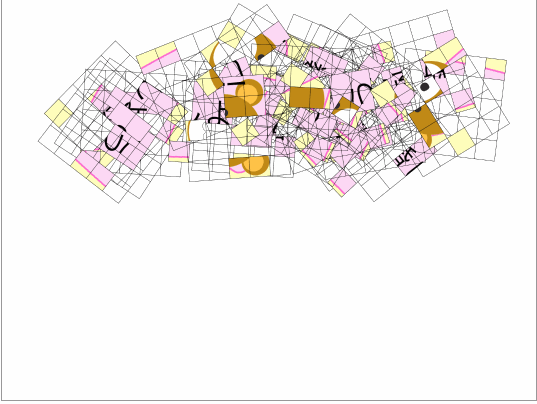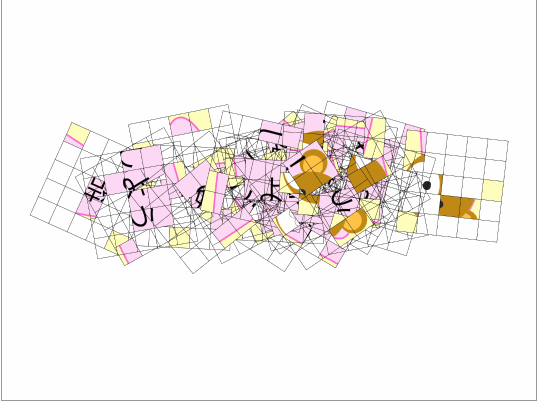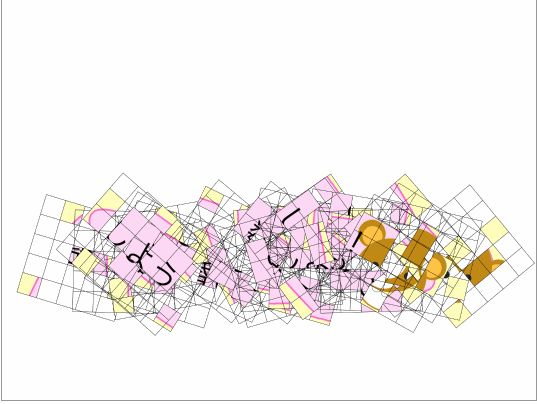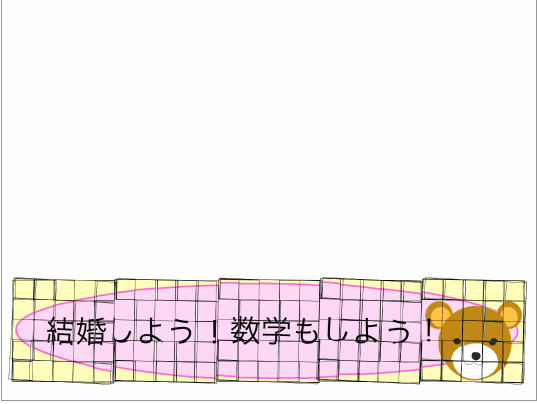
おまけ
今回は有限体上の楕円曲線を可視化しました(←グラフ書いただけ)。可視化すると楕円曲線の方程式を満たす解の個数も一目瞭然ですが、この解の個数がフェルマーの最終定理の証明に深く関係しています。また、この解の個数はハッセ・ヴェイユ境界と呼ばれる、より高度な数学にも関連しています。私はステートメントはなんとなくわかるレベルです。
今回楕円曲線とは何かということに関しては何も触れていません。楕円曲線をgoogle検索すると、やはりtsujimotterさんの記事がwikipediaの次に出てきましたので、ここにも貼り付けておきます。楕円曲線の面白いネタがたくさん書かれています。興味がある方は一緒に楕円曲線の勉強をしましょう。
tsujimotter-sub.hatenablog.com
ついでながら、今回ゴレンジャーのアニメはjavascript、canvasで作成したのですが、画像を回転させるのにこれまたtsujimotterさんの下記の記事が大変役に立ちました。原点を中心としてcanvas全体を回転させるのは簡単にできるのですが、画像を中心として、その画像だけを回転させる方法はネットで調べてもよくわからず、ネットサーフィンを続けているうちに下記の記事に行き着きました。参考にこちらも貼り付けておきます。
