10月1日の第7回日曜数学会で数式お絵描きのパイオニアであるもっちょさんとコロちゃんぬさんが初めて出会う場面、そして数式お絵描きの手法について語り合う場面に立ち会うことができました。私はTwitterアカウント(@mattyuu123)を持っていてもつぶやいたことがなかったのですが、この時初めてつぶやきました。私の中では記念の瞬間でした。
数式お絵描き勉強会#日曜数学会 pic.twitter.com/YUIc2H49rB
— mattyuu (@mattyuu123) 2016年10月1日
私が思うもっちょさんとコロちゃんぬさんの代表作をそれぞれ載せておきます。
やったー!アンパンマンがドラえもんになるグラフができthttps://t.co/0R7niyD4Gy pic.twitter.com/rXleJDdgk6
— 鯵坂もっちょ@通販予定 (@motcho_tw) 2016年1月23日
メタモンのへんしん!https://t.co/hNaGFHTW9b @Desmos pic.twitter.com/I9Mls3ZNdA
— コロちゃんぬ (@corollary2525) 2016年9月25日
この数式お絵描きはdesmosというアプリを用いておられます。私もdesmosを使って何かしてみたいと思い、今回、高校物理の力学、高校数学の範囲でdesmos遊んびしてみたので発表いたします。題材としてはマーライオンを選びました。(数式お絵描きはしておりません)
なお、この記事では高校物理の力学の知識、高校の数Ⅲで習う三角関数の微分の知識を前提としています。前提知識がない方でも、フジテレビのガリレオで福山雅治さんはこんな数式を書いていたんじゃないか?と想像しながら、数式を流し読みしていただけたらと思います。
今回の問題は下記です。

マーライオンが水を噴射するときに、一番遠くまで水を飛ばすには口をどの角度にして発射したらよいかという問題になります。
この問題ではマーライオンの身長(正確には口の高さ)をというパラメータで含めております。実は
、つまり地面から直接水を発射する場合であれば、この問題はとても簡単です。高校物理の力学の最初の方に必ず習うと言ってもいいかもしれません。答えは皆さんのご想像通り45°になります。しかし、身長が加わるだけでこの問題は難しくなります。立式は容易ですが、解けるかがわからないのです。数値解であれば容易に出せますが、解析解を出せるかは、冷や汗ものでした。
解く前に一点注意として、この問題では水は大きさのない質点として計算していきます。また空気抵抗も考えません。水は常に連続的に噴射され続けていますが、時刻で水分子が1粒発射されたものとして読んでください。
では解いていきましょう。
(しばらく単調な計算が続きますので、流れだけ簡単に説明すると、
「時刻での水の位置を求める」→「水が地面に落ちる時刻
を求める」→「水が地面に落ちた時の位置を求める」→「水が地面に落ちた時の位置を発射角
の関数と思って微分する」→「微分を0とする
が答えとなる」)
解くためには、座標軸の設定が必要ですので、次の通りとします。

まずは、口から飛び出る水の速度を水平方向(x軸右方向)の速度と、垂直方向(y軸上方向)の速度
に分けて考えましょう。水平方向には力が加わりませんので、口から飛び出た瞬間の速度のまま変化しません。しかし垂直方向の速度に関しては、重力の影響を受け、時刻
が1増えるごとに重力加速度
ずつ小さくなっていきます。
よって、時刻での速度はそれぞれ下記になります。
次に時刻での水の位置
を出しましょう。高校力学では公式として学んでおり式を導くことができますが、実は、速度を時間で積分することで位置を出すことができます。逆に位置を時間で微分することで速度を出すこともできます。ここでは積分で位置を導きます。公式で覚えている方は結果が一致していることを確認してもいいかもしれません。
、
はそれぞれ左辺の積分を行った結果出てくる、水の時刻
での初期位置になります。水は
より発射されているため、
、
となっております。この
、
を連立させ
を消去することで、
と
の関係を
という二次関数の形で表すことができます。これは、二次関数が放物線と言われる所以(ゆえん)になります。今回の計算では二次関数の形にする必要がないのでこれ以上は立ち入りません。
次に、水が地面に落ちる時刻を求めます。これは
となる
を求めればよいということになります。
とすると、
中学校で習った二次関数の解の公式を、それなりに現実っぽい問題を解く時に使えるのは嬉しいですね。より、水が地面に着く時間
は、
となります。
水が地面に落ちた位置をとしましょう。つまり、
です。
は次の式で表すことができます。
ここで、今後計算を進めるにあたって記載を容易にするために、としています。今考えている変数は
だけであり、
、
、
はそれぞれ定数ですので、このように置いてしまって中身が分からなくなってもこの後の計算には影響しません。
このを
変数の関数
と思って、その最大値を求めていきます。最大、最小を求める方法は微分が定石です。微分して得られる導関数を0とする
が、最大、または最小を与えます。
微分を0にするを求めたいため、
とおき、両辺を
で割ることで、下記のようになります。
が出てきおります、、、これを満たす
を求めることはできるのでしょうか。。。
まずはを含むものと、含まないもので分けましょう。
両辺にをかけましょう。
両辺を二乗しましょう。
途中計算間違いしそうな、ややこしい式変形を経て、なんとも綺麗な形になりました。さて、これ以上先に進めますでしょうか?
進めるんです!
まず、最初の2項は次のように変形できます。
ここで、「和と差の積は二乗の差」と中学時代に呪文のように習った展開(因数分解)の公式と、高校で習う、及び
の加法定理である
が役に立っております。
なんと基礎学力が大事かがわかる場面でしょうか!
私が中学校の先生であったなら、「この因数分解はマーライオンが吐き出す水を解析するために必要なんだよ」と生徒たちに教えたいところです。
後ろの1項はどうでしょうか?
こちらも高校で習う、の加法定理を応用することで、
と変形できます。(を用いてます。)
以上から、は、
となります。ここで、であったことを思い出すと、最終的に、
なんとも、綺麗にまとまった式でしょうか!
高校生の皆さんは、「求めたい答えは、をとると
となる角度を半分にしたものです。」と答えれば正解になります。
大学ではという関数が登場し、
をとると
になる角度を
と表すことができます。
よって、
とできるので、最終的な答え(求めたい角度をとでも名前をつけましょう)をまとめると、次のようになります。

前回記事に書いたトーナメントの数式同様、今回も無事解析解を得ることができたことはなんとも不思議であります。うまく式変形ができなければ、コンピュータによる数値解しか得られなかった可能性は大いにあるのです。
さて、忘れかけていたdesmosを使う時がついにきました。desmosを使って、マーライオンにいろいろな角度で水を発射してもらいましょう。そして今回求めた飛距離が最大になる角度の方向にはオレンジ色の点線を引き、最大到達地点(には赤い旗を置いておきましょう。
そうすると下記のようになり、たしかに今回求めた解析解が正しそうということがわかっていただけるかと思います。
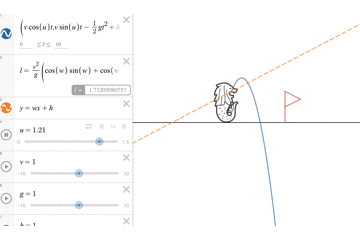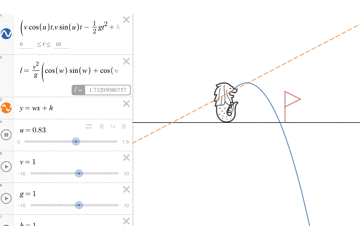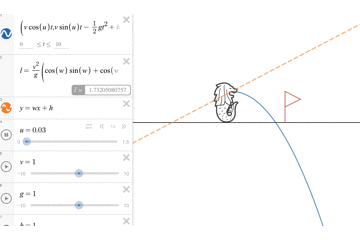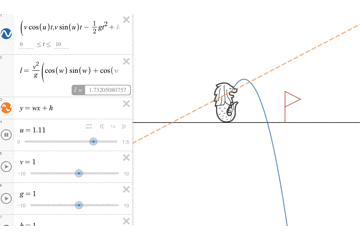
初速をもっと大きくしても、下記のように問題なさそうですね。

今回私が作成したdesmosは下記リンクから遊ぶことができます。
https://www.desmos.com/calculator/vhvcloibx9
もっちょさんやコロちゃんぬさんに比べたらとても簡単なものですが、このように解析した結果をアニメーションで見ることができることには感動を覚えます。私が学生時代であれば、Javaを使って水の軌道を数値計算し、gnuplotを使って静的な画像を何枚も作っていたことでしょう。
また、この数式は小便小僧やサクランボの種飛ばし世界選手権(あるんですね、、)でもそのまま使えます(さくらんぼの種は質点ではなく剛体なので、別の力学を用いる必要がある点には目をつむります)。数学の力を感じますね。
読んでいただき、ありがとうございました。